Parquet with pentagons

The 15 previously known types of flat tiling with congruent, convex pentagons

The tiling with pentagons (also tiling / paving / area connection with pentagons ) is a seamless, overlap-free geometric and monohedral tiling , in which all elements (tiles) are congruent (congruent) to each other and of the shape of one and the same pentagon .

The case of even tiling with congruent (congruent) , convex pentagons is particularly interesting because the shapes (types) in question have been studied for a century, these are not conclusively classified and 5 of the 15 different types currently known by the amateur - Mathematician Marjorie Rice and a computer scientist , inspired by articles by Martin Gardner in the popular science journal Scientific American , were found.

Monohedral tiling with n corners ( n = 3, n = 4, n ≥ 6)

In contrast to the pentagons, the question of the monohedral tiling of the plane with n gons for n ≠ 5 has been completely clarified.

All forms of triangles and convex squares "tile the plane".

With respect to the polygons having a number of corners proved Reinhardt in 1918, that it on the one hand exactly three types of convex hexagons are (hexagons), which can parkettieren, and that it is otherwise impossible to plane with a convex heptagon (heptagon), octagon (octagon) or a higher polygon. ${\displaystyle n\geq 6}$

Monohedral tiling of the plane with pentagons

In contrast to the tiling with other convex polygons, the tiling of the plane with pentagons has not yet been finally clarified. See also section on the work of Michaël Rao .

Designations

With the monohedral tiling one demands congruence among the tiling tiles, but only similarity with the proto tile . Depending on the number of degrees of freedom of the tile type, there may be dissimilar log tiles that belong to the same tile type. The tile type is characterized by a system of relationships between angles on the one hand and aspect ratios on the other. A tile type can have tiled floors with different essential properties.

A congruent pentagon is determined by seven determiners (7 independent parameters), a similar one by six. For similar pentagons, length ratios (of corresponding sides and diagonals) and corresponding angles are the same. If you have four (corner) angles, then the fifth is always determined by the sum of the angles of the pentagon of 540 °.

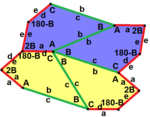
In the following, the (sizes of) angles are denoted by capital letters A, B, C, D, E, so that A + B + C + D + E = 540 °. The orientation is by default the "mathematical", ie counterclockwise (although there are many types with tiling in which both orientations occur). (The lengths of) sides that run towards a corner in this direction of rotation are usually designated with the corresponding small letter, so that, for example, b is the length of the side AB.

The closed nature of the BCDEAB traverse requires:

c cos (B) - d cos (B + C) + e cos (B + C + D) + a cos (-A) = b and

c sin (B) - d sin (B + C) + e sin (B + C + D) + a sin (-A) = 0.

History

After Reinhardt's dissertation, who described the first 5 pentagonal types in 1918, 50 years passed before the topic was taken up again from the late 1960s to the mid-1980s and expanded to include 9 types. Then 30 years passed before another pentagon type, Type 15, was found in 2015 using a computer program specially created for this purpose. The convex pentagons, which are suitable for tiling a plane in a congruent way, can be divided into 15 disjoint classes (types) so far.
It is currently not clear whether there are more such types of pentagons.

Regular pentagon

Nevertheless, statements have been made on special aspects:

• The tiling of a Euclidean plane with regular pentagons is impossible, since with a regular pentagon the interior angle 108 ° is not an integral divisor of the full angle 360 °.
• In 1985, Hirschhorn and Hunt published connections for angle sums , which are essential conditions for tiling with pentagons: An equilateral convex pentagon tills if and only if it has two angles, the sum of which is 180 °, or if it is the unique equilateral convex pentagon , which (in the designations of type 7 in the table below) has the angles A≈99.929 °, B≈89.264 °, C≈144.561 °, D≈70.878 ° and E≈135.368 °, where B + 2E = 2C + D = 2A + B + D = 360 °.
• Olga Bagina was able to show that there are only eight convex edge to edge - Parkettierungstypen can give (edge-to-edge tiling), a result that was confirmed but with reference to Bagina, independently of Teruhisa Sugimoto.

In the following, the 15 known types of monohedral tiling of the level with pentagons are roughly in their order of discovery, respectively. presented with ascending type number.

Reinhardt (1918)

The five convex pentagon types by K. Reinhardt (1918)

1	2	3	4th	5
p2 (2222)	pgg (22 ×)	p3 (333)	p4 (442)	p6 (632)
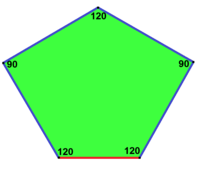
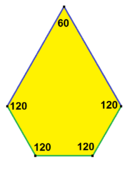
B + C = 180 ° A + D + E = 360 °	c = e B + D = 180 °	a = b, d = c + e A = C = D = 120 °	b = c, d = e B = D = 90 °	a = b, d = e A = 60 °, D = 120 °
2 tile pattern	4-tile pattern	3-tile pattern	4-tile pattern	6 tile pattern

In 1918, Karl Reinhardt , assistant to David Hilbert , dealt in his dissertation with the "decomposition of a plane into equiangular normal polygons belonging to one genus", with particular attention to pentagons and hexagons.

Kershner (1968) and James (1975)

Convex pentagon types
by RB Kershner (1968) and RE James (1975)

6th	7th	8th	10
p2 (2222)	pgg (22 ×)		p2 (2222)
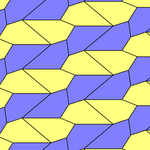
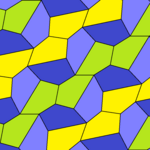
a = d = e, b = c B + D = 180 °, 2B = E	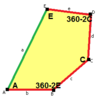b = c = d = e B + 2E = 2C + D = 360 °	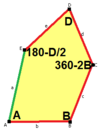b = c = d = e 2B + C = D + 2E = 360 °	a = b = c + e A = 90, B + E = 180 ° B + 2C = 360 °
4-tile pattern	8 tile pattern	8 tile pattern	6 tile pattern
Richard B. Kershner			Richard E. James

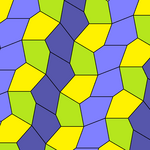
In 1968, the mathematician Richard B. Kershner found three more convex pentagons (types 6 to 8) with which tiling is possible, and came to the conviction that the list of flat pentagons that could be tiled was complete with the eight types now known.

Richard E. James III, then a computer scientist at Control Data Corporation , had read about Kershner's discovery in Martin Gardner's Mathematical Games column in Scientific American and found another pentagon (Type 10) in 1975, thereby refuting Kershner's statement of the complete list. Thanks to James’s approach, it was also possible in retrospect to explain which tiling system Kershner had overlooked.

Rice (1976/77)

The four convex pentagon types by Marjorie Rice (1976/77)

9	11	12	13
pgg (22 ×)
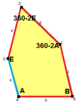b = c = d = e 2A + C = D + 2E = 360 °	2a + c = d = e A = 90 °, 2B + C = 360 ° C + E = 180 °	2a = d = c + e A = 90 °, 2B + C = 360 ° C + E = 180 °	d = 2a = 2e B = E = 90 °, 2A + D = 360 °
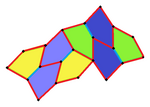8 tile pattern	8 tile pattern	8 tile pattern	8 tile pattern

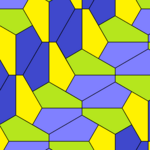
Inspired by Martin Gardner's Mathematical Games column in Scientific American in July and December 1975, Marjorie Rice , a housewife and self-taught mathematician, began to occupy herself with tiling with pentagons. She developed her own notation for pentagons and in this way found another, previously unknown pentagon shape (type 9), which she sent Gardner.
Gardner passed Rice's work on to mathematics professor Doris Schattschneider , who came into contact with Rice and published Rice's results in the following years.

In 1976/77, Rice used her method to discover a total of four new Pentagon types. She also artistically implemented pentagon types by transferring Escher- like image elements to these pentagons: Examples are type 1, type 2 and type 13.

The entrance to the main Mathematical Association of America building in Washington, DC was tiled with one of the pentagons found by Rice in the 1990s.

Stein (1985) and Mann / McLoud / Von Derau (2015)

Convex pentagons by R. Stein (1985) and C. Mann / J. McLoud / D. Von Derau (2015)

14th	15th
p2 (2222)	pgg (22 ×)
2a = 2c = d = e A = 90 °, D = cos −1 ( 3− √ 57 ⁄ 8 ) ≈124.66 ° B = 270 ° −D, C = 360 ° −2B	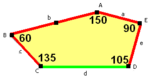a = c = e, b = 2a, d = a √ 2+ √ 3 A = 150 °, B = 60 ° C = 135 °, D = 105 °, E = 90 °
6 tile pattern	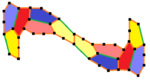12 tile pattern
Stone (1985)	Mann / McLoud / Von Derau (2015)

The German math student Rolf Stein found Type 14 in 1985, which was subsequently analyzed and published by Schattschneider. Its tiles are completely determined.

In 2015, the mathematician couple Casey Mann and Jennifer McLoud and their student David Von Derau from the University of Washington in Bothell discovered a 15th type using a computer program .

They took into account the results of Hirschhorn and Hunt as well as Bagina and used an algorithm that looked for tiling with non-equilateral pentagons that are not edge-to-edge. Von Derau implemented the program and the new pentagon, type 15, was found in the debugging phase.

Michaël Rao (2017)

The fact that no further pentagon was found for two years may be due to the findings of Michaël Rao , according to which a “16. Pentagon ”no longer exists, or is always only a variant of the known 15 pentagons. Since there has not yet been a scientific peer review of his evidence (but positive individual opinions), the search for it may be over - the final confirmation is currently still pending.

Number of degrees of freedom

In his dissertation, Reinhardt classified the tile types according to the length ratios of their five sides:

• RI All five sides are different.
• R-II Among the five pages are two identical; the others are different from these and from each other.
• R-III ₁ Among the five pages are three identical; the others are different from these and from each other.
• R-III ₂ Among the five sides, two pairs are the same, but different from one another; the last is different from these.
• R-IV ₁ Among the five pages, four are the same; the last is different from these.
• R-IV ₂ Among the five sides are three identical and, different from them, two more identical.
• RV All five sides are the same.

All 15 types of tiling described here are isohedral , which means that among the depictions of the tiling on itself there is an image for each pair of tiles that transfers one tile to the other; in short: that the entire tiling “looks the same” from every tile. Many of the 15 types of tiling are multiple isohedral (multiple transitive) .

Type	1	2	3	4th	5	6th	7th	8th	9	10	11	12	13	14th	15th
Degrees of freedom	5	4th	1	2	2	1	1	1	1	1	1	1	1	0	0
Reinhardt class	RI	R-II	R-II	R-III 2	R-III 2	R-IV 2	R-IV 1	R-IV 1	R-II	R-IV 1	R-II	RI	R-II	R-III 2	R-III 1
Edge-to-edge	both	both	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No	No
k -isohedral	1	1	1	1	1	2	2	4th	2	3	2	2	2	3	3
not convex	Yes	Yes	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	Yes	No	No

With tile type 1 there is also non-periodic pentagonal tiling .

Special cases

Non-periodic pentagonal tiling

The staghorn parquet with congruent pentagons

Even non-periodic tiling can be constructed with congruent pentagons, as illustrated in this example (right) with 6-fold rotational symmetry by Michael Hirschhorn with A = 140 °, B = 60 °, C = 160 °, D = 80 °, E = 100 ° .

In 2016, Bernhard Klaassen showed that every rotational symmetry of the plane can be represented by a monohedral tiling of one and the same class of pentagons. Examples of 5-fold and 7-fold rotational symmetry are given here.

Decomposition principle for every n -fold rotational symmetry with n > 2

Pentagonal tiling with 5-fold rotational symmetry

Pentagonal tiling with 7-fold rotational symmetry

All of these examples show, at points where several pentagonal edges can be continued to form a straight line, that periodic tiling is also possible with the underlying pentagonal shape, namely tiling type 1.

Pentagonal tiling of hexagons

Some hexagons can be represented as tiling with pentagons by simple geometric operations.

For example, a regular hexagon can be broken down into two type 1 pentagons by making a vertical cut. Further subdivision into three (type 3), four (type 4) and nine (type 3) congruent pentagons is possible.

Dual pentagonal tiling

There are three isohedral pentagonal tiling (i.e. tiling with a tile-transitory symmetry group) that are dual to tiling of the type shown above. These (dual) tiling are always edge-to-edge and, as a proto-tile, have a special case of higher symmetry among the 15 shown above Tile types.

Tiling dual to type 5	Tiling dual to type 4	Tiling dual to type 5
Prismatic tiling	Cairo tiling	Floret or rosette parquet
Type 1 tile	Type 4 tile	Type 1, 2 and 5 tiles
120 °, 120 °, 120 °, 90 °, 90 ° 1 degree of freedom	120 °, 90 °, 120 °, 90 °, 120 ° b = c = d = e, a = b ( √ 3 -1 )	60 °, 120 °, 120 °, 120 °, 120 ° a = b = 2c = 2d = 2e

Parquet with congruent, concave pentagons in the plane

Fig Pentagon of Livio 2-isohedral

If the congruent pentagons are concave (i.e. not convex), i. In other words , at least one interior corner is truncated (greater than 180 °), then further tiling is possible. One example of this is Livio's Pentagon, for which tiling with extremely different topologies was found.

On page 3 there, Figure 3 shows two (periodic) 1-isohedral tiling : For each pair of pentagons there is a congruence map that transfers one pentagon to the other.

In the (periodic) tiling of the illustration "Pentagon of Livio 2-isohedral", four colors are assigned to the pentagons: dark green, light green, dark red, light red. Parallel shifts and point reflections (rotations by 180 °) depict the pentagons in those of the same color and brightness. The dark pentagons have the same direction of rotation (the very pointed corner is counterclockwise followed by the truncated corner) and the light opposite one. With an axis mirroring, the direction of rotation can be reversed, namely (with an additional parallel shift) light pentagons can be mapped onto dark, same color and vice versa. However, there is no congruence mapping of the tiling that maps green to red pentagons, because with all green pentagons there are two neighboring sides that can be continued as straight lines into the red neighboring pentagons; the red ones also have two such sides, but they are not adjacent. So there are two lines of tiling, the green and the red pentagons, which is why the tiling is to be regarded as a 2-isohedral .

The top right illustration of Figure 4 on page 4 in Tessellations shows an aperiodic tiling with the same pentagon by Livio.

Sphinx tiling ("reptile")

Another example is the so-called Sphinx tiling, an aperiodic tiling with a concave pentagon that is tiled from smaller versions of itself.

Pentagon tiling in hyperbolic geometry

Regular pentagonal tiling

Dodecahedron

A dodecahedron can be understood as the regular tiling of the surface of a sphere with 12 regular pentagons. The associated Schläfli symbol is {5,3}, i. That is, three pentagons are adjacent to each other and each form a corner .

On a hyperbolic level there is an infinite number of tiling with regular pentagons, for example 4th order tiling with the Schläfli symbol {5,4}, i. That is, four pentagons lie next to each other and each form a corner. Higher orders of regular tiling {5, n} can be constructed in this way, theoretically up to {5, ∞}.

Bullet	Hyperbolic level
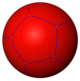{5.3}	{5.4}	{5.5}	{5.6}	{5.7}	{5.8}	... {5, ∞}

Irregular pentagonal tiling

On a hyperbolic level there can be an infinite number of dual-structural, uniform tiling with isogonal, irregular, pentagonal surfaces . According to M. Cundy and A. Rollett, they are described with V3.3.p.3.q.

Orders p - q of the pentagonal Floret tiling

7-3	8-3	9-3	...	5-4	6-4	7-4	...	5-5
V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.9	...	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	...	V3.3.5.3.5	...

Physical supplement: quasicrystals

The strict statement is known from physics that there are sixfold crystal structures, but not fivefold. It was therefore a surprise and was awarded a Nobel Prize in 2011 when Dan Shechtman and co-workers discovered five-fold reflexes in 1984, which are assigned to so-called quasicrystals , a regular, irregular arrangement of incommensurable units (see the links below for details).

literature

• David Wells: The Penguin Dictionary of Curious and Interesting Geometry. Penguin Books, London 1991, ISBN 0-14-011813-6 .
• David Klarner: Mathematical Recreations: A Collection in Honor of Martin Gardner. Dover Publications, Mineola 1998, ISBN 0-486-40089-1 .

See also

• Penrose tiling

Web links

Commons : tiling with pentagons  - collection of images, videos and audio files

• Parquet with pentagons.
• Eric W. Weisstein : Pentagon Tiling . In: MathWorld (English).
• The 14 Different Types of Convex Pentagons that Tile the Plane. (English).
• Tilings with a convex pentagonal tile. (English).

swell

1. ↑ ^{a b c d e f g} Karl Reinhardt: About the division of the plane into polygons. Inaugural dissertation to obtain a doctorate from the High Natural Science Faculty of the Royal University of Frankfurt a. M., Robert Noske, Borna-Leipzig (1918). Please note: There is an error on page 77. The sum of angles γ + δ for the first two types of tiling must be π and not 2π (as indicated).
2. ↑ Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. At: NPR.org. August 14, 2015, accessed August 21, 2015.
3. ↑ ^{a b} M. D. Hirschhorn and DC Hunt: Equilateral convex pentagons which tile the plane. In: Journal of Combinatorial Theory. Series A, Vol. 39 (1), May 1985, pp. 1-18.
4. ↑ ^{a b} Olga Bagina: Мозаики из выпуклых пятиугольников. (Tilings of the plane with convex pentagons.) Vestnik (russ.) (2011), Volume 4 (48), pp. 63–73, ISSN  2078-1768 .
5. ↑ Olga Bagina: Tiling the plane with congruent equilateral convex pentagons. In: Journal of Combinatorial Theory. 2004, Volume 105 (2), pp. 221-232.
6. ↑ Teruhisa Sugimoto: Convex pentagons for edge-to-edge tiling, I. Forma, Volume 27 (1) (2012), pp. 93-103.
7. ^ Richard Kershner: On paving the plane. In: American Mathematical Monthly. Volume 75, pp. 839-844.
8. ↑ George E. Martin: Transformation Geometry: An Introduction to Symmetry . Springer Science & Business Media, April 13, 1982, ISBN 978-0-387-90636-2 , p. 126.
9. ^ M. Gardner: On Tessellating The Plane With Convex Polygon Tiles. In: Scientific American. Volume 233 (1), pp. 112-117, Munn & Company (1975).
10. ^ ^{A b} Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. Volume 51 (1), pp. 29-44 (1978).
11. ↑ ^{a b} Alex Bellos: Attack on the pentagon results in discovery of new mathematical tile. In: TheGuardian.com. August 11, 2015, accessed September 10, 2015.
12. ^ ^{A b} Doris Schattschneider: A new pentagon tiler. In: Mathematics Magazine. 58 (5), p. 308 (1985). This new pentagonal tiling also graced the front of Mathematics Magazine.
13. ↑ Michele Emmer, Doris Schattschneider: MC Escher's Legacy: A Centennial Celebration . Springer, May 8, 2007, ISBN 978-3-540-28849-7 , pp. 244-251.
14. ↑ Roses by Marjorie Rice.
15. ^ Fishes by Marjorie Rice.
16. ↑ Butterflies by Marjorie Rice.
17. ^ Ivars Peterson : Tiling with Pentagons. In: The Mathematical Tourist. June 5, 2010, accessed September 14, 2015.
18. ↑ Derrick Niederman: Number Freak: From 1 to 200 - The Hidden Language of Numbers Revealed . Penguin Publishing Group, August 4, 2009, ISBN 978-1-101-13548-8 , p. 83.
19. ^ Robert Gast: The Magic Pentagon. In: Sueddeutsche.de. August 12, 2015, accessed September 14, 2015.
20. ↑ Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. In: NPR.org. August 14, 2015, accessed September 11, 2015.
21. ↑ Casey Mann: 15th Pentagon. In: reddit.com. August 1, 2015, accessed September 14, 2015.
22. ^ Pentagon Tiling Proof Solves Century-Old Math Problem. At: quantamagazine.org. July 11, 2017. Retrieved July 13, 2017.
23. ↑ 100 year old math puzzle. The end of the pentagonal saga. At: Spektrum.de. July 13, 2017. Retrieved July 13, 2017.
24. ↑ In 6 of the 7 classes of this "Classification of the pentagons" quoted here literally on p. 76, Reinhardt actually uses the word "different". But what is meant is undoubtedly "possibly different", that is, in RI : "the aspect ratio is arbitrary".
25. ↑ Jaap Scherphuis © 2009-2017 Tilings
26. ↑ Tilings with a convex pentagonal tile k - isohedral ( k ∈ {1,2,3,4}) colored tiling with pentagons
27. ^ Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. 1978, Fig. 12.
28. ↑ Bernhard Klaassen: Rotationally symmetric tilings with convex pentagons and hexagons . In: Elements of Mathematics . 71, No. 4, 2016, ISSN  0013-6018 , pp. 137-144. doi : 10.4171 / em / 310 .
29. ^ Bernhard Klaassen: Rotationally Symmetric Tilings with Convex Pentagons and Hexagons . In: arXiv [math] . 2016. arxiv : 1509.06297 .
30. ↑ ^{a b} Chaim Goodman-Strauss: Tessellations (PDF)
31. ^ M. and A. Rollett: Mathematical Models. Tarquin Pub., Stradbroke (England) 1952 (3rd edition 1989), 3.7 The Archimedean Polyhedra. Pp. 101-115 and pp. 118-119, Table I, Nets of Archimedean Duals. V. a . b . c … as vertically-regular symbols.

Comments

1. ↑ Triangles with straight lines are always convex.
2. ↑ The closeness of the equilateral traverse requires:

   cos (B) - cos (B + C) + cos (B + C + D) + cos (A) = 1 and

   sin (B) - sin (B + C) + sin (B + C + D) - sin (A) = 0.

   After the substitutions   B = 360 ° - 2E, D = 360 ° - 2C, A = –180 ° + E + C initially –sin (C) = 2sin (E) / (1–2cos (E)) and finally for x: = 2cos (E)

   x ⁴ - 10x ² + 2x + 19 = 0.

3. ↑ ^{a b c d} Explanations for the table:
   • The first line indicates the type of pentagon ("tile type").
   • The second line indicates the planar crystallographic group (or ornament group ) of a tiling of the plane with this type. However, there may be other tiling that deviate from this.
   • The third line shows a tiling with this pentagon type.
   • The fourth line characterizes a pentagon of the type to be defined by linear equations of aspect ratios, respectively. of angles: all pentagons that meet the conditions below belong to the type. The maximum of six conditions do not define congruence, but at most similarity. If there are fewer than six independent conditions, then dissimilar pentagons are of the same type.
   • The fifth line shows a tile pattern composed of several pentagons of the tile type, from which one of the tiling shown can be produced exclusively through translations .
   • If applicable, the last line names the discoverer (s) of the type.
4. ↑ This second relationship is a direct consequence of the first because of the total angle sum of 540 °. As a result, this type allows five degrees of freedom, for example three angles and two aspect ratios.
5. ↑ Then E + 2D = E + 540 ° -2C = E + 540 ° + B-360 ° = 360 °. So the conditions are invariant to reflection on the Ad axis.
6. ↑ yes = only edge-to-edge; no = there is no edge-to-edge tiling; both = there are both
7. ↑ no = there are only convex tiling
8. ↑ In English Cairo tiling; this type of paving has had this name since 1971 and can actually be found in several places in Cairo , such as on David Bailey's World of Escher-like Tessellations ( memento of the original from October 2, 2015 in the Internet Archive ) Info: The archive link was inserted automatically and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. is documented. 
9. ↑ The name refers to the pattern, which looks like a 6-petalled flower.
10. ↑ It fulfills the conditions:

    a = b = c = d = e and

    2A + E = B + C + 2D = B + C + E = 360 °,

    Conditions that leave no degree of freedom and classify it in convex type 2 . From them it follows first E = 2D, A = 180 ° –D, C = 360 ° –B – 2D, B = 180 ° –3D and because of the closedness of the polygon cos (3D) + cos (2D) +1 = 0, from which one calculates 4cos ² (D) + 2cos (D) -3 = 0, i.e. D = cos ⁻¹ ( ^{√ 13 –1} ⁄ ₄ ) ≈ 49.35368 °.
11. ↑ These geometrical forms, composed of smaller forms of themselves, are introduced by Solomon W. Golomb ( Replicating Figures in the Plane. In: The Mathematical Gazette. Volume 48, No. 366 (1964), pp. 403-412 ) - called rep-tile or reptile in English , a play on words with the term rep etitive tile 'repetitive tile'.