Integer linear optimization

The integral linear optimization (also integral optimization ) is a branch of applied mathematics . Like linear optimization , it deals with the optimization of linear objective functions over a set that is constrained by linear equations and inequalities . The difference is that in integer optimization some or all of the variables may only have integer values and not arbitrary real values as in linear optimization. The integer optimization can be understood geometrically as an optimization over a convex polyhedron (a higher-dimensional polygon) and is thus a special case of convex optimization . In contrast to linear programming, however, the underlying polyhedron is usually not exactly known, which makes the problem NP-difficult from a complexity-theoretical point of view .

Since at least one variable is discrete , i.e. not continuous, the term discrete optimization is also used . Another common name is integer (linear) programming (of English. Integer (linear) programming ), where the term program for the purposes of planning is to understand and not in the sense of a computer program. It was coined by George Dantzig in the 1940s , before computers were used to solve optimization problems.

Since its beginnings in the 1950s, integer optimization has developed even more than linear optimization into a modeling and optimization tool for many practical problems for which no special algorithms are known. Due to significant advances in the development of the solution methods in the 1980s and 1990s, integer optimization has many applications today, for example in production, in planning telecommunications and local transport networks, and in route planning .

To solve integer optimization problems there are, on the one hand, exact solution methods such as branch-and-bound and cutting plane methods , which are based on the solution of many similar linear programs, and, on the other hand, a large number of heuristics . Nevertheless, solving integer linear programs is still a difficult task in practice, which, depending on the size and structure of the problem to be solved, requires skillful modeling and more or less specially developed or adapted algorithms. Therefore, several solution methods are often combined.

Problem definition

Mathematical formulation

An integer linear programming ( English integer program , IP ) has the same shape as a linear program (LP), with the difference that the variables must be integers:

{\ displaystyle \ max _ {x \ in \ mathbb {Z} ^ {n}} \ left \ {c ^ {T} x \; | \; Ax \ leq b, x \ geq 0 \ right \}}

Here is a real matrix and and are vectors of suitable dimensions. The condition is to be understood component-wise, i.e. as ${\ displaystyle A}$ ${\ displaystyle b}$ ${\ displaystyle c}$ ${\ displaystyle Ax \ leq b}$

{\ displaystyle a_ {i} \ cdot x = \ sum _ {j = 1} ^ {n} a_ {ij} x_ {j} \ leq b_ {i}}

for all rows of the matrix . The condition also means that all entries in the vector must be non-negative. Are the integrality for only part of the variables, it is also called a mixed integer program (Engl. Mixed-integer program , MIP ). Also, the precise integer linear program (engl. Integer linear program , ILP) is in use. As in linear optimization, there are several equivalent formulations that can be transformed into one another (see Linear Optimization: Problem Definition ). ${\ displaystyle i}$ ${\ displaystyle A}$ ${\ displaystyle x \ geq 0}$ ${\ displaystyle x}$

Geometric interpretation

The whole-number optimization, like the linear variant, can be interpreted geometrically to a large extent. The amount

{\ displaystyle P: = \ {x \ in \ mathbb {R} ^ {n} \; | \; Ax \ leq b, x \ geq 0 \},}

which arises from the omission of the integer conditions, forms a convex polyhedron in -dimensional space, the limiting hyperplanes of which correspond to the lines of the inequality system. contains u. a. all admissible points of the initial system, i.e. all integer points that meet the conditions , but in contrast to linear optimization, not all points in are admissible. The linear program ${\ displaystyle n}$ ${\ displaystyle P}$ ${\ displaystyle Ax \ leq b}$ ${\ displaystyle P}$

{\ displaystyle \ max \, \ {c ^ {T} x \; | \; x \ in P \}}

is called the LP relaxation of the integer problem and plays an important role in some solution methods (see below ).

Like linear programs, integer programs can also be unsolvable or unlimited. In all other cases there is at least one optimal solution, provided the inequality system only has rational entries. In contrast to real linear optimization, it is possible to construct problems that have no optimal solution, although solutions exist and the objective function is limited. In contrast to LPs, the set of optimal solutions of an IP is not a face of the polyhedron , so that besides exactly one or an infinite number of optimal solutions there can also be another finite number (greater than 1) of them. ${\ displaystyle P}$

Examples

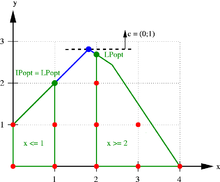
Polytope of permissible integer points (red) with LP relaxation (blue)

In the picture opposite is the integer linear program

{\ displaystyle {\ begin {matrix} \ max && y \\ & - x & + y & \ leq 1 \\ & 3x & + 2y & \ leq 12 \\ & 2x & + 3y & \ leq 12 \\ && x, y \ in \ mathbb {Z} _ {\ geq 0} \ end {matrix}}}

shown. The admissible integer points are drawn in red, and the red dashed lines mark their convex hull , i.e. the smallest polyhedron that contains all these points. This polyhedron should actually be optimized, but it is usually not exactly known. The blue lines together with the coordinate axes delimit the polyhedron of the LP relaxation, which is given by the inequality system without integer conditions. The aim of the optimization is to move the black dashed line parallel upwards (in the direction of the vector ) so far that it just touches the respective polyhedron. The optimal solutions of the integer problem are therefore the points and with the objective function value . The - in this case unambiguous - optimal solution of the LP relaxation with the objective function value 2.8 is the point marked in blue , which is not an integer and is therefore not permissible for the IP. ${\ displaystyle P}$ ${\ displaystyle c = (0; 1)}$ ${\ displaystyle (1; 2)}$ ${\ displaystyle (2; 2)}$ ${\ displaystyle c ^ {T} x = (0; 1) ^ {T} (1; 2) = (0; 1) ^ {T} (2; 2) = 2}$ ${\ displaystyle LP_ {opt} = (1 {,} 8; 2 {,} 8)}$

The following IP is an example of the special case mentioned above:

{\ displaystyle {\ begin {matrix} \ max & - {\ sqrt {2}} x & + y \\ & - {\ sqrt {2}} x & + y & \ leq 0 \\ && x & \ geq 1 \\ && y & \ geq 0 \\ && x, y \ in \ mathbb {Z} \ end {matrix}}}

The admissible solutions such as B. represent rational approximations for in the form . Since is irrational and can therefore be approximated with arbitrary precision, there is no optimal solution, although the objective function is bounded above by the first condition. ${\ displaystyle (10; 14)}$ ${\ displaystyle {\ sqrt {2}}}$ ${\ displaystyle {\ frac {y} {x}}}$ ${\ displaystyle {\ sqrt {2}}}$

Applications

The integer conditions considerably expand the modeling possibilities for practical problems compared to linear optimization. There are two main reasons for integer variables:

For practical reasons, the variables must be integers. For example, 3.7 aircraft cannot be built, but only a whole number.
The integer variables are limited to the values 0 or 1 (so-called binary variables ) and represent decisions. For example, a bus cannot drive a third, only either all of it or not at all.

Often both cases occur together. Integer optimization can be used in many practical fields of application, some of which are briefly described below.

Production planning

In production planning, the problem often arises of determining production quantities for several products that share common resources (machines, working hours, storage capacities ...). The goal is, for example, to maximize the total contribution margin without exceeding the available resources. In some cases this can be expressed using a linear program, but often the variables have to be integers for practical reasons (see above).

Local public transport

In the service and vehicle scheduling in public transport it comes to, for example, buses or subways as to distribute the individual lines that the timetable can be met, and to equip them with drivers. Binary decision variables play a major role here. B. express whether a certain type of bus is traveling on a line or not, or whether a subway driver is assigned to a certain train or not.

Telecommunication networks

The goal of capacity and routing planning in nationwide telecommunication networks is to install capacity on the nodes and lines of a network and to route communication requirements in such a way that all requirements are met and the total costs of the network are minimal. As a rule, the capacity cannot be installed in arbitrary proportions, but only in certain integer units. Depending on the technology used, there are usually other restrictions that can be modeled as linear inequalities with integer or binary variables.

Cellular networks

The task of frequency planning in GSM mobile radio networks is to distribute the available frequencies to the antennas in such a way that all users can be served and the disturbing interference between the antennas is minimized. This problem can be formulated as an integer linear program in which u. a. Binary variables represent whether or not a frequency is assigned to a particular antenna.

Tour planning

The tour , especially the Traveling Salesman Problem , is a classic example of integer programming, whose research has contributed much to the development of general solution process. It is clearly a matter of finding the shortest round trip between a given set of cities. This problem can be modeled as an integer linear program with an exponential number of inequalities. Various extended variants of route planning appear in practice, for example when drilling circuit boards, or when planning travel routes for field staff (e.g. a technical customer service or an insurance company) who want to serve all their customers with the shortest possible routes.

0/1 programming

A particularly important special case of integer optimization is optimization in which the variables are not only allowed to assume integer values, but are limited to the binary values 0 or 1. In this way, the search for solutions for Boolean functions can be transferred to geometry: Finding an assignment of such a function becomes equivalent to finding 0/1 points in the section and the union of high-dimensional polytopes . This method is called disjunctive programming and was developed by Egon Balas in the late 1960s . 0/1 programming is a difficult combinatorial problem and is one of Karp's 21 NP-complete problems .

history

The beginning of integer optimization is closely related to the development of linear optimization in the mid-1940s. In 1947 George Dantzig published several crucial papers on linear optimization and the simplex method , which he developed further in the following years together with John von Neumann and others.

When the first practically applicable computer programs for solving linear programs were developed with the advent of computers in the 1950s, the solvability of integer optimization problems also came within reach. In the mid-1950s, DR Fulkerson , G. Dantzig , and S. Johnson worked on the first cutting levels for the traveling salesman problem. Without knowledge of this work and motivated by former colleagues in the US Navy who were interested in integer solutions, Ralph Gomory developed the first generally applicable cutting plane method in 1958 during his stay in Princeton , which (at least in theory) allowed the complete solvability of any integer programs. Even if this could only be partially implemented in practice, this procedure represented a decisive algorithmic advance.

Shortly afterwards, in 1960, AH Land and AG Doig presented the branch-and-bound method, which is based on a clever enumeration of the search space. In 1965, RJ Dakin specified an algorithm that was easy to implement. Later, Egon Balas largely combined branch-and-bound with cutting plane methods to branch-and-cut , which allowed the solution of significantly larger integer linear programs.

At the end of the 1960s, Egon Balas , among others, developed a general method of finding linear descriptions that only contain integer vertices from the outset. This so-called lift-and-project is based on the idea of relocating the optimization into a high-dimensional space and projecting the solution found into lower dimensions.

In the 1980s, Manfred Padberg and others worked on cutting planes for sub-structures that often arise, such as backpack problems , which can often also be used in a more general context. The enormous algorithmic advances in linear optimization in the 1990s were also reflected in the significantly better solvability of integer programs, since, for example, when using cutting plane methods and branch-and-bound algorithms, a large number of linear programs have to be solved. In addition to better modeling and solution techniques for frequently occurring sub-problems, such as network flows, many heuristics, i.e. approximation methods, were developed in parallel, which mostly calculate permissible solutions in a short time. You can u. a. can also be used as part of branch-and-cut processes to speed them up. All of these methods are still the subject of current research.

Complexity and solution method

In contrast to linear programs , which, for example , can be optimally solved with interior point methods in polynomial time, finding a provable optimal solution for integer programs is a problem with NP. This is also noticeable in practice. While even large linear programs can be solved with standard methods today, the solvability of integer programs depends much more on the specific characteristics of the respective planning problem and on the modeling chosen. An optimization problem with a hundred integer variables can be practically unsolvable, while other problems with thousands of integer variables can be solved in a matter of seconds. There are also standard methods in integer optimization with which many practical planning problems can now be solved as IP due to great algorithmic advances within the last ten years, but the solution of large integer programs in particular often requires skillful modeling and a combination of several Solution procedures with problem-specific adaptations.

Exact and heuristic procedures

When classifying the algorithms, a distinction must be made between exact and heuristic solution methods.

Heuristic methods typically deliver feasible solutions in a relatively short time, but no information about how good these are compared to an optimal solution. If a heuristic does not find a solution, it is not known whether this is due to the algorithm or whether the optimization problem under consideration is in principle unsolvable. Heuristic procedures are mostly adapted to the problem to be solved, such as the k-opt heuristics for the problem of the traveling salesman. In the case of metaheuristics such as taboo search , the basic process is generic, but the individual steps of the algorithm must be defined depending on the problem under consideration.

Exact methods can be proven to always find an optimal solution or determine that the problem is unsolvable or unlimited, provided that the algorithm is allowed to run for any length of time. Examples of this are branch-and-bound, cutting plane methods and their combination of branch-and-cut. In practice, these procedures can often be accelerated significantly by adapting them to the problem to be solved and by combining them with heuristics. An elegant way to quickly find an exact solution is to model the search space - the convex polyhedron in n-dimensional space that contains all possible solutions - in such a way from the start that it only contains integer extreme points. This is the case , for example, for totally unimodular matrices . The polyhedron is therefore not subsequently reduced with cutting planes. If this succeeds - for example through lift-and-project - then the optimization task can simply be solved, for example, by executing the simplex algorithm .

Dual bounds and proof of optimality

Upper and lower bounds

All practically relevant exact methods are based on the iterative solution and modification of a relaxation , i.e. a simpler problem whose solution set contains all the solutions of the original problem. For example, branch-and-bound and cutting plane methods use LP relaxation, so initially leave out the integer conditions. This can also be interpreted geometrically: Actually, an optimal corner of the IP polyhedron (dashed red in the picture above) is sought, which is spanned by all permissible integer points. Since this polyhedron is usually not exactly known, an optimal corner of the polyhedron of the LP relaxation is sought instead , which contains (in the example above, outlined in blue). This is relatively easy, e.g. B. with the simplex method. ${\ displaystyle P_ {I}}$ ${\ displaystyle P}$ ${\ displaystyle P_ {I}}$

Since more solutions are allowed in the relaxation than in the initial problem, its optimal value is at least as high (in the case of a maximization problem) as the - unknown - optimal value of the IP, thus providing an upper (generally: dual ) bound for this . At the same time, the value of every feasible integer solution defines a lower (generally: primal ) bound for the value of an optimal solution, since this is by definition at least as good as . By comparing the upper and lower bounds, a maximum relative distance, the so-called optimality gap, between the value of a solution found and the optimal value can be specified without knowing this exactly. ${\ displaystyle L}$ ${\ displaystyle L}$

In the example above, the optimal value of the LP relaxation is 2.8. The optimal value of the integer problem cannot be higher, since fewer solutions are allowed there than in the LP relaxation. The point that can be found, for example, by guessing or using a heuristic, is a feasible solution of the integer problem and has the objective function value 1. An optimal solution is by definition at least as good as the solution found. So the optimal value of the integer problem must be between 1 and 2.8. The absolute optimality gap is the difference between the upper and lower bound, in this case the relative optimality gap given more frequently results from normalizing this value with the lower bound, in this case as it says that the optimal value of the integer program is at most 180% higher lies than the value of the solution . This allows a quality assessment of the solution (not particularly good in this case). The actual difference is , i. H. the optimal value is twice as high as the value of the solution found. ${\ displaystyle (1; 1)}$ ${\ displaystyle (2 {,} 8-1) = 1 {,} 8.}$ ${\ displaystyle 1 {,} 8/1 = 1 {,} 8 = 180 \, \%.}$ ${\ displaystyle (1; 1)}$ ${\ displaystyle (2-1) / 1 = 1 = 100 \, \%}$

In the course of the algorithm, the relaxation is gradually tightened (for example by adding additional inequalities) so that the resulting upper bound becomes smaller and smaller. At the same time, an attempt is made to find better feasible solutions to raise the lower bound. This is illustrated in the adjacent figure. If the value of a found solution and the dual bound are the same (in the example with the value 2), this is the proof that the found solution is optimal.

In the following some important exact and heuristic solution methods are presented in more detail.

Cutting plane method

Adding a cutting plane (green)

Cutting-plane method ( English cutting plane algorithm ) first compute a solution to the LP relaxation. This is usually not an integer, but provides a dual limit for the optimal value of the IP. This dual barrier is then tightened by gradually adding so-called cutting planes . A cutting plane is an additional inequality that is satisfied by all feasible points of the IP, but not by the current LP solution. If the inequality is added to the LP, another solution must come out when the solution is again. This is continued until an integer solution is found (which is then automatically also optimal for the integer program) or no more suitable inequalities are found.

Geometrically, this procedure corresponds to the addition of a hyperplane, which cuts the optimal corner of the LP polyhedron from the (unknown) polyhedron that is spanned by the integer solutions. When you solve the problem again, an optimal corner of the trimmed polyhedron is determined. If this is an integer, a permissible and optimal solution of the integer linear program has been found. Otherwise a new cutting plane is searched for. ${\ displaystyle P}$

The image on the right shows the cutting plane (green) that separates ( separates ) the previous LP optimum (blue) from the IP polyhedron . All permissible points lie on one side of the hyperplane, the LP solution on the other side. Solving the LP again with this additional inequality yields the point marked in green (4/3; 7/3). This point is still not permissible, but has the smaller objective function value 7/3, which for example reduces the relative optimality gap for the solution (1; 1) from 180% to . ${\ displaystyle x + 2y \ leq 6}$ ${\ displaystyle (7 / 3-1) / 1 = 4/3 \ approx 133 \, \%}$

In practical application, cutting plane methods are an important aid, but are usually not sufficient on their own and can lead to numerical problems if used carelessly. Instead, they are often combined with branch-and-bound. How well this works depends heavily on the structure of the problem being solved. The best cutting planes one can find are facets of the IP polyhedron. In the example above, these are the inequalities and , which correspond to the red dashed lines. In order to identify such inequalities, a more detailed mathematical investigation of the underlying polyhedron is usually necessary. ${\ displaystyle y \ leq 2}$ ${\ displaystyle x + y \ leq 4}$

Branch-and-Bound or Branch-and-Cut

Branching on the variable x

Also branch and bound begins with the release of the LP relaxation. If the solution obtained is not an integer, the problem is broken down into two or more sub-problems in such a way that each feasible solution is contained in one of these sub-problems. In this way, a branch tree is built with the LP relaxation as the root node. (At each branch English branch the range of values of one or more variable) regions. This is done until a best integer solution has been found.

In this pure form the procedure corresponds to a complete enumeration of all possible solutions. With the help of the dual bounds that are obtained by solving the relaxations at each node of the branching tree, however, subtrees can be cut off ( bound ) if it turns out that they cannot contain an optimal solution. Branch-and-bound is usually not sufficient as the sole algorithm, because too little can be cut off from the search tree. Good IP solvers therefore combine this method with cutting plane methods to improve the dual bound. This approach is then called branch-and-cut .

In the adjacent example, based on the broken LP solution , the two sub-problems are considered that arise from adding the additional condition or . Each admissible solution is contained in exactly one of the two partial polyhedra (outlined in green). Solving the LP relaxation with the additional conditions provides the fractional solution with the objective function value in the right subproblem and the integer solution with the value 2 in the left subproblem . This improves the lower bound for the optimal IP value to 2 (the value of the best known feasible solution), while the upper bound is reduced to (the higher LP value of the two sub-problems). The optimality gap is thus reduced to , i. H. the optimal value is at most times as high as the value of the solution . In fact, this solution is already optimal since it is an integer solution to a relaxation of the original problem. ${\ displaystyle (1 {,} 8; 2 {,} 8)}$ ${\ displaystyle x \ leq 1}$ ${\ displaystyle x \ geq 2}$ ${\ displaystyle (2; 8/3)}$ ${\ displaystyle 8/3}$ ${\ displaystyle (1; 2)}$ ${\ displaystyle 8/3}$ ${\ displaystyle (8 / 3-2) / 2 = 1/3}$ ${\ displaystyle (1 + 1/3)}$ ${\ displaystyle (1; 2)}$

Lagrange relaxation

The Lagrangian relaxation is a process from the nonlinear optimization that can be applied to the integer optimization. The basic idea is to leave out "disturbing" inequalities so that the remaining problem (with integer constraints) can be easily solved, and instead to punish the violation of these inequalities, weighted with so-called Lagrange multipliers , in the objective function.

A solution to this simpler problem will in most cases not meet the conditions relaxed in the objective function. In order to change this, the Lagrange multipliers are adjusted with the help of a sub-gradient method depending on the current (inadmissible) solution so that a new solution with the new weights generates a somewhat “more admissible” solution that violates the relaxed inequalities less strongly. This process is repeated iteratively until all conditions are met. It can be shown that every solution of a Lagrange relaxation yields a dual bound for the original IP, and that this method converges with a suitable adjustment of the multipliers.

Heuristics

For almost every optimization problem, it is easy to find a multitude of heuristics that quickly find permissible solutions for this particular problem. In contrast, the development of heuristic methods that reliably find good solutions, and if possible also for a whole class of related optimization problems and not just for a special problem, is a non-trivial task.

Examples of problem-specific heuristics for the traveling salesman problem are the minimum spanning tree heuristic for constructing a permissible tour with the help of a minimal spanning tree and the k-opt heuristics for improving a tour that has already been found. This optimization problem is also one of the few examples in which heuristic dual bounds can easily be given. For example, every tour through nodes also contains exactly edges, so that a shortest tour must be at least as long as the sum of the shortest edge lengths. In general, it is much more difficult to give good dual bounds. ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$

In addition to such methods specially developed for a problem, there are so-called metaheuristics that describe strategies for searching for permissible solutions in a problem-independent manner. However, the individual steps of these algorithms must be specially adapted to the problem to be solved. Examples are the rounding of LP solutions, local searches , taboo searches , evolutionary algorithms , simulated annealing , variable neighborhood searches and ant algorithms . Some of these methods are modeled on processes such as natural selection or the behavior of ants in search of food; The extent to which this is of advantage for the solution quality and the solution times in practice is controversial.

As the sole solution method, all these algorithms have the disadvantage that, firstly, they do not always find a solution, and secondly, mostly nothing is known about the quality of the solutions found in comparison to an optimal solution. However, they can, for example, be used very sensibly as part of a branch and cut approach in order to generate good, permissible solutions at various nodes in the search tree, for example from the current LP solution, and thus to be able to cut off parts of the tree.

literature

Books

Wolfgang Domschke, Andreas Drexl, Robert Klein, Armin Scholl: Introduction to Operations Research . 9th edition. Springer, Berlin 2015, ISBN 978-3-662-48215-5 (especially chapter 6).
Josef Kallrath: Mixed-integer optimization. Modeling in Practice . Vieweg, Wiesbaden 2002, ISBN 3-528-03141-7 .
Richard K. Martin: Large Scale Linear and Integer Optimization. A unified approach . Kluwer Academic Publishers, Boston, Mass. 2004, ISBN 0-7923-8202-1 .
George Nemhauser, Laurence Wolsey: Integer and Combinatorial Optimization . Wiley Interscience, New York 1999, ISBN 0-471-35943-2 .
Leena Suhl, Taieb Mellouli: Optimization Systems. Models, processes, software, applications . Springer, Berlin 2006, ISBN 3-540-26119-2 .

Essays

Robert J. Dakin: A tree-search algorithm for mixed integer programming problems . In: The Computer Journal , Vol. 8 (1965), pp. 250-255.
Ralph Gomory: Early Integer Programming . In: Operations Research , Vol. 50 (2002), number 1, pp. 78-81.
Ailsa H. Land, Alison G. Doig: An automatic method of solving discrete programming problems . In: Econometrica , Vol. 28 (1960), pp. 497-520.

Web links

Linear Programming FAQ section on Integer Programming (English)
Comparison of non-commercial codes for solving MIPs by Hans Mittelmann, Arizona State University, with links to the codes
Optimization in practice (English)