Artificial neural network
Artificial neural networks , also called artificial neural networks , in short: KNN (English artificial neural network , ANN), are networks of artificial neurons . They are the subject of research in neuroinformatics and represent a branch of artificial intelligence .

Artificial neural networks, like artificial neurons, have a biological model. They are contrasted with natural neural networks , which represent a network of neurons in the nervous system of a living being. However, ANNs are more about an abstraction ( modeling ) of information processing and less about the replication of biological neural networks and neurons, which is more the subject of computational neuroscience .
description
Artificial neural networks are mostly based on the networking of many McCulloch-Pitts neurons or slight modifications thereof. In principle, other artificial neurons can also be used in ANNs, e.g. B. the high-order neuron . The topology of a network (the assignment of connections to nodes) must be well thought out depending on its task. After the construction of a network, the training phase follows, in which the network “learns”. In theory, a network can learn through the following methods:
- Development of new connections
- Deleting existing connections
- Changing weights (the weights from neuron to neuron )
- Adjusting the threshold values of the neurons, provided that these have threshold values
- Adding or deleting neurons
- Modification of activation, propagation or output functions
In addition, the learning behavior changes when the activation function of the neurons or the learning rate of the network changes. In practical terms, a network “learns” mainly by modifying the weights of the neurons. An adaptation of the threshold value can also be done by an on-neuron . As a result, ANNs are able to learn complex non-linear functions using a "learning" algorithm that tries to determine all parameters of the function from existing input and desired output values using an iterative or recursive approach . ANNs are a realization of the connectionist paradigm , since the function consists of many simple similar parts. The behavior in the interaction of a large number of parts involved can only become complex when combined. In terms of predictability, neural networks represent an equivalent model to the Turing machine .
historical development
Interest in artificial neural networks began as early as the early 1940s , roughly at the same time as the use of programmable computers in applied mathematics.
Beginnings
The beginnings go back to Warren McCulloch and Walter Pitts . In 1943, these describe links between elementary units as a type of network similar to the networking of neurons, with which virtually any logical or arithmetic function could be calculated. In 1947 they point out that such a network can be used, for example, for spatial pattern recognition. In 1949 Donald O. Hebb formulated his Hebbian learning rule , which in its general form represents most of the artificial neural learning processes. In 1950 Karl Lashley came up with the thesis that the process of storing information in the brain was distributed across different subunits.
First heyday
In the following year, 1951, Marvin Minsky succeeded with his dissertation in building the Snarc neurocomputer , which can automatically adjust its weights, but is not practical. In 1956, scientists and students meet at the Dartmouth Conference . This conference is considered to be the birth of Artificial Intelligence as an academic subject. From 1957 to 1958, Frank Rosenblatt and Charles Wightman developed the first successful neurocomputer, named Mark I Perceptron . The computer could already recognize simple digits with its 20 × 20 pixel image sensor. In the following year Rosenblatt formulates the Perceptron-Convergence Theorem . In 1960, Bernard Widrow and Marcian E. Hoff presented the ADALINE ( ADAptive LInear NEuron ). This network was the first to achieve wide commercial distribution. It was used in analog telephones for real-time echo filtering. The neural network learned with the delta rule . In 1961 Karl Steinbuch presented techniques of associative storage. In 1969, Marvin Minsky and Seymour Papert gave an accurate mathematical analysis of the perceptron . They showed that important problems cannot be solved. Among other things, XOR operators cannot be resolved and there are problems with linear separability . The result was a temporary end to research in the field of neural networks, as most of the research funds were canceled.
Slow rebuilding
In 1972 Teuvo Kohonen presented the linear associator , a model of the associative memory. James A. Anderson describes the model independently of Kohonen from a neuropsychological point of view in the same year. 1973 Christoph von der Malsburg uses a neuron model that is non-linear. As early as 1974 Paul Werbos developed backpropagation or error tracing for his dissertation . But the model only became more important later. From 1976 Stephen Grossberg developed mathematically based models of neural networks. Together with Gail Carpenter , he also devotes himself to the problem of keeping a neural network capable of learning without destroying what has already been learned. You formulate an architecture concept for neural networks, the adaptive resonance theory . In 1982 Teuvo Kohonen describes the self-organizing cards named after him . In the same year, John Hopfield describes the model of the Hopfield networks . In 1983 Kunihiko Fukushima , S. Miyake and T. Ito presented the neocognitron neural model . The model is a further development of the Cognitron developed in 1975 and is used to recognize handwritten characters.
Renaissance
In 1985 John Hopfield published a solution to the Traveling Salesman problem through a Hopfield network . In 1985, the learning procedure Backpropagation of Error was developed separately as a generalization of the delta rule by the parallel distributed processing group. Thus, problems that cannot be linearly separated can be solved by multilayer perceptrons . Minsky's assessment was therefore refuted.
New successes in pattern recognition competitions since 2009
Recently, neural networks have seen a rebirth, as they often deliver better results than competing learning methods in challenging applications. Between 2009 and 2012, the recurrent or deep forward neural networks of Jürgen Schmidhuber's research group at the Swiss AI laboratory IDSIA won a series of eight international competitions in the fields of pattern recognition and machine learning . In particular, their recurrent LSTM networks won three related handwriting recognition competitions at the 2009 Intl. Conf. on Document Analysis and Recognition (ICDAR) without built-in a priori knowledge of the three different languages to be learned. The LSTM networks learned simultaneous segmentation and recognition. These were the first international competitions to be won through deep learning or recurrent networks.
Deep forward-looking networks like Kunihiko Fukushima's convolution network of the 80s are important again today. They have alternating Konvolutionslagen ( convolutional layers ) and layers of neurons, summarized (several activations pooling layers ) to the spatial dimension to reduce. Such Konvolutionsnetz usually is completed by several fully connected layers ( English fully connected layers ). Yann LeCun's team from New York University applied the back- propagation algorithm , which was already well known in 1989, to such networks. Modern variants use so-called max-pooling for the combination of the activations, which always gives preference to the strongest activation. Fast GPU implementations of this combination were introduced in 2011 by Dan Ciresan and colleagues in Schmidhuber's group. Since then they have won numerous competitions, including a. the "ISBI 2012 Segmentation of Neuronal Structures in Electron Microscopy Stacks Challenge" and the "ICPR 2012 Contest on Mitosis Detection in Breast Cancer Histological Images". Such models also achieved the best results to date on the ImageNet benchmark. GPU-based max-pooling convolution networks were also the first artificial pattern recognizers with superhuman performance in competitions such as the "IJCNN 2011 Traffic Sign Recognition Competition".
Interconnect network topology
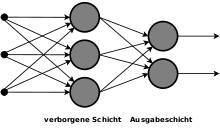
In artificial neural networks, the topology describes the structure of the network. This generally means how many artificial neurons are on how many layers and how they are connected to one another. Artificial neurons can be connected in a variety of ways to form an artificial neural network. In this case, the neurons are many models in successive layers ( English layers arranged); a network with only one trainable neuron layer is called a single-layer network .
Using a graph , the neurons can be represented as nodes and their connections as edges . The entries are sometimes also shown as nodes.
The rearmost layer of the network, the neuron outputs are visible mostly as only one outside of the network, output layer (English output layer ) called. Front of it layers are respectively as hidden layer (English hidden layer hereinafter).
Typical structures
The structure of a network is directly related to the learning method used and vice versa; only a single-layer network can be trained with the delta rule ; a slight modification is necessary for several layers. Networks do not necessarily have to be homogeneous: there are also combinations of different models in order to combine different advantages.
There are pure feedforward networks in which one layer is only ever connected to the next higher layer. In addition, there are networks in which connections are permitted in both directions. The appropriate network structure is usually found using the trial and error method , which can be supported by evolutionary algorithms and error recovery .
- Single-tier feedforward network
- Single-layer nets with the feed forward property (English for forward ) the simplest structures of artificial neural networks. They only have an output layer. The feedforward property means that neuron outputs are only routed in the processing direction and cannot be fed back through a recurrent edge ( acyclic , directed graph ).
- Multi-layer feedforward network
- In addition to the output layer, multilayer networks also have hidden layers, the output of which, as described, is not visible outside the network. Hidden layers improve the abstraction of such networks. Only the multi-layer perceptron can solve the XOR problem.
- Recurrent network
- In contrast, recurrent networks also have backward (recurrent) edges ( feedback loops ) and thus contain feedback . Such edges are then often provided with a time delay so that the neuron outputs of the previous unit can be reapplied as inputs during step-by-step processing. These feedbacks enable a network to behave dynamically and provide it with a memory .
In certain brain regions of mammals - and also other vertebrates, such as songbirds - neurons are formed and integrated into the neural network not only in developmental stages, but also in adulthood (see adult neurogenesis , especially in the hippocampus ). In the attempt to artificially simulate such processes in neural networks, the modeling reaches its limits. It is true that an evolutionary algorithm , similar to a Moore machine , can determine how often a neuron has to be activated so that new neurons form in the environment. However, it must also be specified here how the new neurons are to be integrated into the existing network. Artificial neural networks of this type must inevitably do without being built up in layers. You need a completely free structure, for which at best the space in which the neurons can be located can be limited.
application
Its special properties make the ANN interesting for all applications in which there is little or no explicit (systematic) knowledge about the problem to be solved. These are e.g. B. text recognition , speech recognition , image recognition and face recognition , in which a few hundred thousand to millions of pixels have to be converted into a comparatively small number of permitted results.
Also in the control technology ANN are used to conventional controllers to replace them or setpoints to pretend that the power of a self-developed forecasting over the course of the process is determined. Fuzzy systems can also be designed to be capable of learning through bidirectional conversion into neural networks.
The possible applications are not limited to technology-related areas: when predicting changes in complex systems, ANNs are used as support, e.g. B. for the early detection of looming tornadoes or to estimate the further development of economic processes.
The areas of application of ANNs include in particular:
- Regulation and analysis of complex processes
- Early warning systems
- Error detection
- optimization
- Time series analysis (weather, stocks, etc.)
- Speech synthesis
- Sound synthesis
- classification
- Image processing and pattern recognition
- Computer science : For robotics , virtual agents and AI modules in games and simulations
- Medical diagnostics , epidemiology and biometrics
- Structural equation model for modeling social or business relationships
Despite this very large range of application areas, there are areas that ANNs cannot cover due to their nature, for example:
- Prediction of random or pseudo-random numbers
- Factoring large numbers
- Determining whether a large number prim is
- Decryption of encrypted texts
Implementations
- TensorFlow - program library
- SNNS - Stuttgart Neural Network Simulator
- EpsiloNN neural description language of the University of Ulm
- OpenNN
Biological motivation
While the brain is capable of massive parallel processing, most of today's computer systems only work sequentially (or partially in parallel with a computer). However, there are also the first prototypes of neural computer architectures, so to speak the neural chip, for which the research field of artificial neural networks provides the theoretical basis. The physiological processes in the brain are not reproduced, but only the architecture of the massively parallel analog adders in silicon, which promises better performance compared to software emulation.
Classes and types of ANN
Basically, the classes of the networks mainly differ in terms of the different network topologies and connection types, for example single-layer, multi-layer, feedforward or feedback networks.
- McCulloch-Pitts Nets
- Learning matrix
- Perceptron
- Self-Organizing Maps (also Kohonen networks) (SOM)
- Growing Neural Gas (GNG)
- Learning vector quantization (LVQ)
- Boltzmann machine
- Cascade Correlation Networks
- Counterpropagation networks
- Probabilistic neural networks
- Radial basis function networks (RBF)
- Adaptive Resonance Theory (ART)
- Neocognitron
-
Spiking Neural Networks (SNN)
- Pulse-Coded Neural Networks (PCNN)
- Time Delay Neural Networks (TDNNs)
-
Recurrent Neural Networks (RNNs)
- Bidirectional Associative Memory (BAM)
- Elman networks (also Simple recurrent network, SRN)
- Jordan networks
- Oscillating neural network
Activation function
Each hidden layer and the output layer or its neurons have their own activation function. These can be linear or non-linear. Non-linear activation functions make the network particularly powerful.
Learning process
Learning methods are used to modify a neural network in such a way that it generates associated output patterns for certain input patterns. This is basically done in three different ways.
Supervised learning
In supervised learning, the ANN is given an input pattern and the output that the neural network produces in its current state is compared with the value that it should actually output. By comparing the target and actual output, conclusions can be drawn about the changes to be made to the network configuration. The delta rule (also known as the perceptron learning rule) can be used for single-layer perceptrons . Multi-layer perceptrons are usually trained with backpropagation , which is a generalization of the delta rule.
Unsupervised learning
Unsupervised learning takes place exclusively by entering the patterns to be learned. The neural network changes by itself according to the input patterns. There are the following learning rules:
Reinforced learning
It is not always possible to have the appropriate output data set available for training for every input data set. For example, an agent who has to find their way around in a strange environment - such as a robot on Mars - cannot always be told which action is best. But you can give the agent a task that he should solve independently. After a test run, which consists of several time steps, the agent can be evaluated. An agent function can be learned on the basis of this evaluation.
The learning step can be accomplished through a variety of techniques. Among other things, artificial neural networks can also be used here.
Stochastic learning
- Simulated annealing ( simulated annealing )
General problems
The main disadvantages of ANN at the moment are:
- The training of ANNs (in the term of statistics: the estimation of the parameters contained in the model ) usually leads to high-dimensional, non-linear optimization problems. The fundamental difficulty in solving these problems in practice is often that one cannot be sure whether one has found the global optimum or just a local one. Although a large number of local optimization methods that converge relatively quickly have been developed in mathematics (for example quasi-Newton methods : BFGS, DFP, etc.), these too rarely find optimal solutions. A time-consuming approximation to the global solution can be achieved by repeating the optimization many times with always new starting values.
- Training data must be collected or generated manually. This process can be very difficult, as one has to prevent the network from learning properties of the patterns which are correlated in some way with the result on the training set, but which cannot or should not be used for decision-making in other situations. If, for example, the brightness of training images shows certain patterns, the network may no longer 'pay attention' to the desired properties, but only classify the data based on the brightness. In the social field z. For example, there is the risk of continuing existing discrimination (e.g. on the basis of gender or origin) through unilaterally selected test data without sufficiently taking into account the actually targeted criteria (e.g. creditworthiness).
- Upon application of a heuristic approach to network specification KNN tend to learn the training data simply by heart due Overgeneralization or overfitting ( English overfitting ). When this happens, the networks can no longer generalize to new data. In order to avoid over-adaptation, the network architecture must be chosen carefully. This problem also exists in a similar way with many other statistical methods and is referred to as the distortion-variance dilemma . Improved procedures use boosting , support vector machines or regularization to counter this problem.
- The coding of the training data must be adapted to the problem and, if possible, be chosen without redundancy. The form in which the data to be learned is presented to the network has a major influence on the learning speed and on whether the problem can be learned from a network at all. Good examples of this are voice data, music data or even texts. Simply feeding in numbers, for example from a .wav file for speech, rarely leads to a successful result. The more precisely the problem is posed by preprocessing and coding alone, the more successfully an ANN can process it.
- The pre-assignment of the weights plays an important role. As an example, assume a 3-layer feed-forward network with an input neuron (plus a bias neuron ) and an output neuron and a hidden layer with N neurons (plus a bias neuron). The activation function of the input neuron is the identity. The activation function of the hidden layer is the tanh function. The activation function of the output layer is the logistic sigmoid . The network can learn a maximum of one sine function with N local extrema in the interval from 0 to 1. When it has learned this sine function, it can learn any function with this weight assignment - the no more local extrema than this sine function - with possibly exponential acceleration (regardless of the learning algorithm). The simplest backpropagation without momentum is used here. Fortunately, one can easily calculate the weights for such a sine function without the network having to learn it first: Hidden layer:, x = i% 2 == 0? 1: -1 ; Output layer: .
Film documentaries
- Artificial Neural Networks - Computers Learn to See, Simple Explanation, 2017
- Artificial neural networks, more complex explanation
- Artificial Neural Networks - Learning Programs, Simple Explanation, 2017
See also
literature
- Johann Gasteiger , Jure Zupan: Neural Networks in Chemistry and Drug Design. Wiley-VCH, Weinheim NY et al. 1999, ISBN 3-527-29779-0 .
- Simon Haykin: Neural Networks. A Comprehensive Foundation. 2nd edition, international edition = reprint. Prentice-Hall, Upper Saddle River NJ et al. 1999, ISBN 0-13-273350-1 .
- John Hertz, Anders Krogh, Richard G. Palmer: Introduction to the Theory of Neural Computation. Emphasis. Addison-Wesley, Reading MA et al. 1999, ISBN 0-201-51560-1 ( Santa Fé Institute studies in the sciences of complexity. Lecture notes 1 = Computation and neural systems series ).
- Teuvo Kohonen : Self Organizing Maps. 3rd edition. Springer, Berlin et al. 2001, ISBN 3-540-67921-9 ( Springer Series in Information Sciences 30 = Physics and Astronomy online library ).
- Rudolf Kruse , Christian Borgelt, Frank Klawonn , Christian Moewes, Georg Ruß, Matthias Steinbrecher: Computational Intelligence. 1st edition, Vieweg + Teubner Verlag / Springer Fachmedien Wiesbaden, 2011, ISBN 978-3-8348-1275-9 .
- Burkhard Lenze: Introduction to the mathematics of neural networks. With C application programs on the Internet. 3rd revised and revised edition. Logos-Verlag, Berlin 2009, ISBN 3-89722-021-0 .
- André Lucas: Estimation and Specification of Econometric Neural Networks. Eul, Lohmar 2003, ISBN 3-89936-183-0 ( series: Quantitative Ökonomie 138), (also: Köln, Univ., Diss., 2002).
- Heinz Rehkugler, Hans Georg Zimmermann: Neural networks in the economy. Fundamentals and financial applications. Vahlen, Munich 1994, ISBN 3-800-61871-0 .
- Günter Daniel Rey, Karl F. Wender: Neural Networks. An introduction to the basics, applications and data analysis. Hogrefe AG, Bern 2018, third edition, ISBN 978-34568-5796-1 ( psychology textbook ).
- Helge Ritter , Thomas Martinetz , Klaus Schulten: Neural Computation and Self-Organizing Maps. An Introduction. Addison-Wesley, Reading MA 1992, ISBN 0-201-55442-9 ( Computation and Neural Systems Series ).
- Raúl Rojas : Theory of Neural Networks. A systematic introduction. 4. corrected reprint. Springer, Berlin et al. 1996, ISBN 3-540-56353-9 ( Springer textbook ).
- Andreas Zell: Simulation of neural networks. 4. Unchanged reprint. Oldenbourg, Munich et al. 2003, ISBN 3-486-24350-0 .
Web links
- Introduction to the basics and applications of neural networks
- "A look into neural networks , July 1, 2019, in: Fraunhofer Institute for Telecommunications
- "Neural Networks: Introduction", Nina Schaaf, January 14, 2020 , in: Informatik Aktuell (magazine)
- A brief overview of neural networks - basic script for numerous types / learning principles of neural networks, many illustrations, simply written, approx. 200 pages ( PDF ).
- Good introduction to neural networks (English)
Individual evidence
- ↑ - ( Memento of the original from May 2, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ http://www.dkriesel.com/science/neural_networks , as of April 14, 2016
- ^ Warren S. McCulloch and Walter Pitts: A logical calculus of the ideas immanent in nervous activity . Ed .: Bulletin of Mathematical Biophysics. Vol. 5 edition. Kluwer Academic Publishers, 1943, p. 115-133 , doi : 10.1007 / BF02478259 .
- ↑ a b Neural Networks - Introduction. Retrieved September 5, 2015 .
- ↑ Erhard Konrad: On the history of artificial intelligence in the Federal Republic of Germany (PDF; 86 kB), accessed on May 23, 2019.
- ^ Bernhard Widrow, Marcian Hoff : Adaptive switching circuits. In: Proceedings WESCON. 1960, ZDB -ID 267416-6 , pp. 96-104.
- ^ Marvin Minsky , Seymour Papert : Perceptrons. An Introduction to Computational Geometry. MIT Press, Cambridge MA et al. 1969.
- ^ Teuvo Kohonen: Correlation matrix memories. In: IEEE transactions on computers. C-21, 1972, ISSN 0018-9340 , pp. 353-359.
- ↑ James A. Anderson: A simple neural network generating an interactive memory. In: Mathematical Biosciences. 14, 1972, ISSN 0025-5564 , pp. 197-220.
- ↑ 2012 Kurzweil AI Interview ( Memento of the original from August 31, 2018 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. with Jürgen Schmidhuber on the eight competitions that his deep learning team won between 2009 and 2012
- ↑ Alex Graves, Jürgen Schmidhuber: Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. In: Yoshua Bengio, Dale Schuurmans, John Lafferty, Chris KI Williams, Aron Culotta (Eds.): Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th – 10th, 2009, Vancouver, BC. Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545-552
- ↑ A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber: A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, Volume 31, No. 5, 2009.
- ^ Y. Bengio: Learning Deep Architectures for AI. ( Memento of the original from March 21, 2014 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. Now Publishers, 2009.
- ^ Jürgen Schmidhuber : My First Deep Learning System of 1991 + Deep Learning Timeline 1962–2013.
- ↑ K. Fukushima: Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position . In: Biological Cybernetics . 36, No. 4, 1980, pp. 93-202. doi : 10.1007 / BF00344251 .
- ↑ Dominik Scherer, Andreas Müller, Sven Behnke: Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition . In: Artificial Neural Networks - ICANN 2010 (= Lecture Notes in Computer Science ). Springer Berlin Heidelberg, 2010, ISBN 978-3-642-15825-4 , p. 92-101 , doi : 10.1007 / 978-3-642-15825-4_10 ( springer.com [accessed August 26, 2019]).
- ↑ Y. LeCun, B. Boser, JS thinkers, D. Henderson, RE Howard, W. Hubbard, LD Jackel: backpropagation Applied to Handwritten Zip Code Recognition. In: Neural Computation. Volume 1, 1989. pp. 541-551.
- ↑ M. Riesenhuber, T. Poggio: Hierarchical models of object recognition in cortex. In: Nature Neuroscience. 1999.
- ^ DC Ciresan, U. Meier, J. Masci, LM Gambardella, J. Schmidhuber: Flexible, High Performance Convolutional Neural Networks for Image Classification. International Joint Conference on Artificial Intelligence (IJCAI-2011, Barcelona), 2011.
- ^ D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In: Advances in Neural Information Processing Systems (NIPS 2012), Lake Tahoe, 2012.
- ↑ D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Mitosis Detection in Breast Cancer Histology Images using Deep Neural Networks. MICCAI 2013.
- ↑ A. Krizhevsky, I. Sutskever, GE Hinton: ImageNet Classification with Deep Convolutional Neural Networks. NIPS 25, MIT Press, 2012.
- ^ MD Zeiler, R. Fergus: Visualizing and Understanding Convolutional Networks. 2013. arxiv : 1311.2901
- ^ DC Ciresan, U. Meier, J. Schmidhuber : Multi-column Deep Neural Networks for Image Classification. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012.
- ^ DC Ciresan, U. Meier, J. Masci, J. Schmidhuber: Multi-Column Deep Neural Network for Traffic Sign Classification. Neural Networks, 2012.
- ↑ Neural Networks FAQ. Retrieved July 24, 2019 .
- ↑ Neural Networks FAQ. Retrieved September 5, 2015 .
- ↑ Johannes Merkert: I built an artificial neural network myself. In: c't. Retrieved May 24, 2016 .