Artificial neuron
An artificial neuron forms the basis for the model of artificial neural networks , a model from neuroinformatics that is motivated by biological neural networks . As a connectionist model , they form an artificial neural network in a network of artificial neurons and can thus approximate functions of any complexity , learn tasks and solve problems where explicit modeling is difficult or impossible to carry out. Examples are face and speech recognition .
As a model based on the biological model of the nerve cell , it can process several inputs and react accordingly via its activation . For this purpose, the inputs are weighted and transferred to an output function which calculates the neuron activation. Their behavior is generally given to them through learning using a learning process .
history

The beginnings of artificial neurons go back to Warren McCulloch and Walter Pitts in 1943. Using a simplified model of a neural network, the McCulloch-Pitts cell , they show that it can calculate logical and arithmetic functions.
The Hebb rule of learning is described by Donald Hebb in 1949 . Based on the medical research of Santiago Ramón y Cajal , who proved the existence of synapses as early as 1911 , active connections between nerve cells are repeatedly strengthened according to this rule. The generalization of this rule is still used in today's learning processes.
An important work comes out in 1958 with the convergence theorem about the perceptron . There Frank Rosenblatt shows that with the specified learning process he can teach in all the solutions that can be represented with this model.
However, the critics Marvin Minsky and Seymour Papert show in 1969 that a single-stage perceptron cannot represent an XOR operation because the XOR function cannot be linearly separated (linearly separable); only later models can remedy this problem. The limit shown in the modeling initially leads to a decreasing interest in researching artificial neural networks and to a cancellation of research funds.
An interest in artificial neural networks only reappeared when John Hopfield made the Hopfield networks known in 1985 and showed that they were able to solve optimization problems such as the traveling salesman problem . The work on the backpropagation method by David E. Rumelhart , Geoffrey E. Hinton and Ronald J. Williams from 1986 onwards also leads to a revival of research into these networks.
Today such nets are used in many research areas.
Biological motivation
Artificial neurons are motivated by the nerve cells of mammals, which are specialized in receiving and processing signals. Signals are passed on electrically or chemically to other nerve cells or effector cells (e.g. for muscle contraction ) via synapses .
A nerve cell consists of the cell body , axon and dendrites . Dendrites are short cell processes that are highly branched and take care of the reception of signals from other nerve cells or sensory cells . The axon functions as the signal output of the cell and can reach a length of 1 m. The transition of the signals takes place at the synapses, which can have an exciting or inhibiting effect.
The dendrites of the nerve cell transmit the incoming electrical excitations to the cell body. If the excitation reaches a certain limit value and exceeds it, the tension is discharged and propagated via the axon ( all-or-nothing law ).
The interconnection of these nerve cells forms the basis for the intellectual performance of the brain . According to estimates, the human central nervous system consists of 10 10 to 10 12 nerve cells with an average of 10,000 connections - the human brain can therefore have more than 10 14 connections. The action potential in the axon can propagate at a speed of up to 100 m / s.
In comparison to logic gates , the efficiency of neurons can also be seen. While gates switch in the nanosecond range (10 −9 ) with an energy consumption of 10 −6 joules (data from 1991), nerve cells react in the millisecond range (10 −3 ) and only use energy of 10 −16 joules. Despite the apparently lower values in the processing by nerve cells, computer-aided systems cannot match the capabilities of biological systems.
The performance of neural networks is also demonstrated by the 100-step rule : Visual recognition in humans takes place in a maximum of 100 sequential processing steps - the mostly sequential computers do not provide comparable performance.
The advantages and properties of nerve cells motivate the model of artificial neurons. Many models and algorithms for artificial neural networks still lack a directly plausible, biological motivation. There this is only found in the basic idea of the abstract modeling of the nerve cell.
Modeling
With biology as a model, a solution that can be used for information technology is now being found through suitable modeling . A rough generalization simplifies the system - while maintaining the essential properties.
The synapses of the nerve cell are mapped by adding weighted inputs, and the activation of the cell nucleus by an activation function with a threshold value. The use of an adder and threshold value can already be found in the McCulloch-Pitts cell of 1943.
Components
An artificial neuron with the index and the n inputs, indexed with , can be described by four basic elements:
- Weighting : Each input is given a weight. The weights(inputat neuron) determine the degree of influence that the inputs of the neuron have in the calculation of the later activation . Depending on the sign of the weights, an input can have an inhibitory or exciting ( excitatory ) effect. A weight of 0 marks a nonexistent connection between two nodes.
- Transfer function: The transfer function calculates the network input of the neuron based on the weighting of the inputs .
- Activation function: The output of the neuron is ultimately determined by the activation function. The activation is influenced by the network input from the transfer function and a threshold value .
- Threshold: Adding a threshold to the network input shifts the weighted inputs . The designation results from the use of a threshold value function as an activation function, in which the neuron is activated when the threshold value is exceeded. The biological motivation here is the threshold potential in nerve cells. From a mathematical point of view, the parting plane that separates the feature space is shifted by a threshold value with a translation .
The following elements are defined by a connection graph:
-
Inputs: Inputs can result from the observed process, the values of which are transferred to the neuron, or come from the outputs of other neurons. They are also represented like this:

- Activation or output : The result of the activation function is referred to as activation (o for "output") of the artificial neuron with the index , analogous to the nerve cell .
Mathematical definition
The artificial neuron as a model is usually introduced in the literature in the following way:
First, the artificial neuron is activated (referred to as "network input" or "net" in the illustration above)
Are defined. Since mathematics generally does not differentiate between the index (0..9) and the number (10), a synthetic input is usually introduced as a mathematical simplification and one writes
It is
- the number of entries
- the entry with the index , both discrete and continuous may be
- the weighting of the input with the index
- the activation function and
- the output
Activation functions
Different function types can be used as activation functions , depending on the network topology used . Such a function can be non-linear, for example sigmoid , piecewise linear or a step function. In general, activation functions are monotonically increasing .
Linear activation functions are very limited, since a composition of linear functions can be represented by arithmetic transformations by a single linear function. They are therefore not suitable for multilayer connection networks and are only used in simple models.
Examples of basic activation functions are:
Threshold function
The threshold function ( engl. Hard limit ), as defined hereinafter, taking only the values or at. The value 1 for the input , otherwise . If a threshold is used subtractively , the function is only activated if the additional input exceeds the threshold. A neuron with such a function is also called a McCulloch-Pitts cell . It reflects the all-or-nothing nature of the model.
A neuron with this activation function is also represented like this: ![]()
Piecewise linear function
The here used piecewise linear function (engl. Piecewise linear ) forms a limited interval from linear, the outer intervals are mapped to a constant value:
A neuron with the piecewise linear function as the activation function is also represented as follows: ![]()
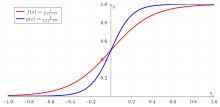
Sigmoid function
Sigmoid functions as activation functions are very frequently used images. As defined here, they have a variable slope that influences the curvature of the function graph . A special property is their differentiability , which is required for some methods such as the backpropagation algorithm:
The values of the above functions are in the interval . These functions can be defined accordingly for the interval .
A neuron with sigmoid function is also represented like this: ![]()
Rectifier (ReLU)
Rectifier as an activation function is used particularly successfully in deep learning models. It is defined as the positive part of their argument.
Examples
Representation of Boolean functions
Boolean functions can be represented with artificial neurons . The three functions conjunction ( and ), disjunction ( or ) and negation ( not ) can be represented using a threshold function as follows:
| conjunction | Disjunction | negation |
|---|---|---|
 Neuron that represents the conjunction |
 Neuron that represents the disjunction |
 Neuron that represents the negation |
For the conjunction, for example, it can be seen that only for the Boolean entries and the activation
results, otherwise .
Learning a neuron
Unlike in the previous example, in which the appropriate weightings were selected, neurons can learn the function to be represented. The weights and threshold are initially randomized and then adjusted using a " trial and error " learning algorithm.
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
In order to learn the logical conjunction, the perceptron criterion function can be used. It adds the values of incorrectly recognized inputs to the weighting in order to improve recognition until as many inputs as possible are classified correctly. The activation function here is the threshold function analogous to the previous example .
The learning rate, which determines the speed of learning, is also selected for the learning process . An explicit mention is therefore not required.
Instead of specifying the threshold value as such, an on neuron ( bias ), i.e. a constant input, is added. The threshold is indicated by the weighting .
To the neuron to the two possible outputs and to train the conjunction, the entries are for the associated output with multiplied. The output is only through this step if the relevant input was classified incorrectly. This procedure simplifies the consideration during teaching and the subsequent adjustment of the weighting. The learning table then looks like this:
| Inputs | ||
|---|---|---|
| −1 | 0 | 0 |
| −1 | 0 | −1 |
| −1 | −1 | 0 |
| 1 | 1 | 1 |
At the inputs, the input has the value at which the neuron should output at the end .
For the initial situation, the weightings are chosen randomly:
| Weight | Initial value | meaning |
|---|---|---|
| ( ) | 0.1 | Representation of the threshold |
| 0.6 | Weighting of the first entry | |
| −0.3 | Weighting of the second input |
To test the weights, they are inserted into a neuron with three inputs and the threshold value . For the selected weights, the output looks like this:
| Inputs | output | |||
|---|---|---|---|---|
| −1 | 0 | 0 | 0 | |
| −1 | 0 | −1 | 1 | |
| −1 | −1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | |
The first and third inputs are calculated incorrectly and the neuron outputs . Now the perceptron criterion function is used:
By adding the incorrectly recognized entries, the associated weights are determined by
- corrected.
It is
- the number of the entry,
- the desired output,
- the actual output,
- the input of the neuron and
- the learning speed coefficient.
|
|
|||||||||||||||||||||||||||||||||||||||
The check after the weighting change shows that instead of the first and third input, the fourth input is classified incorrectly. Carrying out a further step in the learning process improves the neuron's recognition function:
|
|
|||||||||||||||||||||||||||||||||||||||
You can now see that the neuron has learned the given function and has correctly calculated all four inputs.
Using the input and and the selection of the activation follows:
For the other three inputs, which were multiplied by for teaching , the value now results . So follows from the input and the activation:
Without specifying certain weightings, the neuron has learned to use the specifications to represent the conjunction as in the first example.
Application force of a single neuron
An artificial neuron is able to learn by machine even without an entire network. The statistical terms are linear regression and classification. In this way, linear functions can be learned and linearly separable classes can be distinguished. With the help of the so-called kernel trick, non-linear models can also be learned. According to this, a single neuron can produce results similar to, but not optimally, SVMs.
literature
- Simon Haykin : Neural Networks, A Comprehensive Foundation . Macmillan College Publishing Company, New York 1994, ISBN 0-02-352761-7 .
- Andreas Zell: Simulation of neural networks . R. Oldenbourg Verlag, Munich 1997, ISBN 3-486-24350-0 .
- Jürgen Cleve, Uwe Lämmel: Data Mining . De Gruyter Oldenbourg Verlag, Munich 2014, ISBN 978-3-486-71391-6 .
- Jürgen Cleve, Uwe Lämmel: Artificial Intelligence . Hanser Verlag, Munich 2012, ISBN 978-3-446-42758-7 .
Web links
swell
- ↑ JJ Hopfield, D. Tank: Neural Computation of Decisions in Optimization Space . Biological Cybernetics, No. 52, pp. 141-152, 1985.
- ↑ Patricia S. Churchland , Terrence J. Sejnowski: Basics of neuroinformatics and neurobiology. Friedr. Vieweg & Sohn Verlagsgesellschaft, Braunschweig / Wiesbaden 1997, ISBN 3-528-05428-X
- ↑ Werner Kinnebrock: Neural Networks: Basics, Applications, Examples. R. Oldenbourg Verlag, Munich 1994, ISBN 3-486-22947-8































![[0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![[-1, + 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/daa72f1a806823ec94fda7922597b19cbda684f4)






























