Cubic iteration

This item has been on the quality assurance side of the portal mathematics entered. This is done in order to bring the quality of the mathematics articles to an acceptable level . Please help fix the shortcomings in this article and please join the discussion !  ( Enter article )

The cubic iteration falls within the domain of discrete dynamics in the complex plane .

Julia sets to polynomials

Each polynomial defines a mapping of the complex plane in itself. If you choose a starting point , you can see where it is transported through. If the respective end point is selected recursively as the starting point, a complex-valued sequence is obtained , at . In the usual notation for multiple concatenations of an image with itself, the following applies . ${\displaystyle p\in \mathbb {C} [X]}$ ${\displaystyle z_{0}\in \mathbb {C} }$ ${\displaystyle p}$ ${\displaystyle (z_{k})_{k\in \mathbb {N} }}$ ${\displaystyle z_{k}=p(z_{k-1})}$ ${\displaystyle (z_{k})_{k\in \mathbb {N} }=\left(p^{k}(z_{0})\right)_{k\in \mathbb {N} }}$

According to the general theory of the iteration of rational functions, one can divide the points of the complex plane according to whether the sequence shows the same behavior for all in a small environment; these form the Fatou set of the iteration. Those points for which there are points with radically different behavior of the sequence in every small neighborhood form the Julia set . The Julia set is the boundary of every connected component of the Fatou set. ${\displaystyle z_{0}}$ ${\displaystyle \left(p^{k}(z)\right)_{k\in \mathbb {N} }}$ ${\displaystyle z\approx z_{0}}$ ${\displaystyle z_{0}}$ ${\displaystyle z}$

In graphic representations, the Fatou component, which contains the infinitely distant point, and its complement, the Fatou component of the restricted orbits, are used instead of the fractal edge, which is difficult to determine

${\displaystyle \operatorname {F} _{p}:=\left\{z_{0}\in \mathbb {C} \colon \sup _{k\in \mathbb {N} }|p^{k}(z_{0})|<\infty \right\}}$

shown and suitably colored.

Amount of almond bread

One can now distinguish the polynomials according to whether their Julia set is topologically connected or not. In order to obtain a representable structure from this, one must choose a subset of the set of all polynomials that can be represented by at most three real parameters. In order to gain as large an overview as possible, it should be avoided that polynomials with similar Julia sets are included in the parameterization. A simple similarity arises from the shift or generally linear transformation of the Julia set. A bounded sequence also yields by a linear transformation , a bounded sequence . If it is different from zero, the reverse statement also applies. ${\displaystyle (z_{k})_{k\in \mathbb {N} }}$ ${\displaystyle w=qz+r,q,r\in \mathbb {C} }$ ${\displaystyle (w_{k})_{k\in \mathbb {N} }}$ ${\displaystyle q}$

If the sequence was created by a polynomial dynamic , the sequence is also created by a polynomial dynamic of the same degree. The associated polynomial results from the initial polynomial according to ${\displaystyle (z_{k})_{k\in \mathbb {N} }}$ ${\displaystyle p}$ ${\displaystyle (w_{k})_{k\in \mathbb {N} }}$ ${\displaystyle p}$

${\displaystyle w_{k+1}=q\,z_{k+1}+r=q\cdot p(z_{k})+r=q\cdot p\left(q^{-1}\cdot (w_{k}-r)\right)+r}$

as . In the context of this article, each resulting polynomial is called linear equivalent to . ${\displaystyle p_{(q,r)}(X):=q\cdot p(q^{-1}\,(X-r))+r,\ d\in \mathbb {C} }$ ${\displaystyle p(X)}$

Be of degree , . The leading two coefficients of result in ${\displaystyle p(X)}$ ${\displaystyle d}$ ${\displaystyle p(X)=p_{d}X^{d}+\dots +p_{1}X+p_{0}}$ ${\displaystyle p_{(q,r)}(X)}$

${\displaystyle p_{(q,r),d}=q^{1-d}p_{d}}$and . ${\displaystyle p_{(q,r),d-1}=q^{1-d}(q\,p_{d-1}-dr\,p_{d})}$

So in every class of linear equivalent polynomials one can find one whose two leading coefficients are 1 and 0. To do this, select such that and apply. Since there are different solutions for , each linear equivalent class has equivalent representatives. The Julia sets belonging to the different representatives are created by rotating apart. ${\displaystyle q,r}$ ${\displaystyle q^{d-1}=p_{d}}$ ${\displaystyle r\,dp_{d}=qp_{d-1}}$ ${\displaystyle (d-1)}$ ${\displaystyle q}$ ${\displaystyle (d-1)}$

Grade two

If one examines the Julia sets of the quadratic polynomials, each class of linear isomorphic polynomials is represented by a polynomial . The representation of the classification of the connected Julia sets yields, with , the classic Mandelbrot set . There is only a first root of unity, so there are no symmetries of the Mandelbrot set apart from the one resulting from the complex conjugation. ${\displaystyle p(X)=X^{2}+p_{0}}$ ${\displaystyle p_{0}=-c}$

Grade three

The classes of linear equivalent cubic polynomials are represented by the polynomials . There are two such representatives in each class, since there are two second roots of unity and . The second polynomial is . Similar to the classical Mandelbrot set, the decision as to whether the Julia set of a polynomial is topologically connected can be traced back to the membership of the critical points in the Julia set. is critical point of when holds. The derivative is quadratic, so there are two critical points. If the pair of a critical point and the constant coefficient is chosen as the parameterization, then the polynomials are obtained . ${\displaystyle p(X)=X^{3}+p_{1}X+p_{0}}$ ${\displaystyle q=1}$ ${\displaystyle q=-1}$ ${\displaystyle -p(-X)=X^{3}+p_{1}X-p_{0}}$ ${\displaystyle p(X)}$ ${\displaystyle p(X)}$ ${\displaystyle a}$ ${\displaystyle p}$ ${\displaystyle p^{\prime }(a)=3a^{2}+p_{1}=0}$ ${\displaystyle p(X)=X^{3}-3a^{2}X+b{\mbox{ mit }}a,b\in \mathbb {C} }$

The polynomials for the pairs and generate, with the exception of one rotation, the same Julia set, so the Mandelbrot set for this parameterization has, in addition to the symmetry through complex conjugation, a four-fold symmetry. ${\displaystyle (a,b),(a,-b),(-a,b)}$ ${\displaystyle (-a,-b)}$ ${\displaystyle S}$

Sections through the three-dimensional body

Sections through the three-dimensional body

The amount of Mandelbrot is described by: ${\displaystyle S}$

${\displaystyle S=\left\{(a,b)\in \mathbb {C} ^{2}|\forall z_{0}\in \{+a,-a\};{\mbox{ }}\sup _{k\in \mathbb {N} }|p^{k}(z_{0})|<\infty ;{\mbox{ bei }}p(z)=z^{3}-3a^{2}z+b\right\}}$

Polynomials are a special case . In this case, the cactus fractal is obtained as a Mandelbrot-like amount. ${\displaystyle P(x)=x^{3}+(c-1)x-c}$

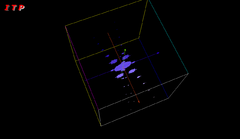
Visualization

The problem with the visualization of this set is that the parameter space is complex two- and thus real four-dimensional. One helps here z. B. by selecting one of the four parameters and setting it to a fixed value. The other parameters are understood as coordinates in a three-dimensional space. This method is a three-dimensional step in four-dimensional space.

Travel through the parameter space of cubic polynomials

In order to capture the fourth dimension after all, it can be reintroduced as time. I.e. you create single images for an ascending sequence of the fourth parameter and summarize them in an animation. In this way you get a film that shows a journey through a set interval on the “fourth axis”.

The set has a fractal surface and shows strong parallels with the Mandelbrot set. If you make two-dimensional cuts on the three-dimensional objects that are created, you will find the characteristic shape of the apple male in some places in these cutting planes. ${\displaystyle S}$

literature

• Bodil Branner, John H. Hubbard : The iteration of cubic polynomials Part I: The global topology of parameter space, Acta Mathematica, Volume 160, 1988, pp 143-206, Project Euclid
• Bodil Branner, John H. Hubbard: The iteration of cubic polynomials Part II: patterns and parapatterns, Acta Mathematica, Volume 169, 1992, pp. 229-325, Project Euclid
• John Milnor : Remarks on iterated cubic maps, Experimental Mathematics, Volume 1, 1992, pp. 5-24, Project Euclid

Web links

Cubic Iterations 3D (program for visualizing the parameter space)

Individual evidence

1. ↑ Cactus Fractal (MathWorld)