Multi-track Turing machine

A multi-track Turing machine ( English Multi-track Turing machine ) is an abstract machine in the theoretical computer science and an expansion of the classical Turing machine .

3 track Turing machine

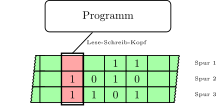
The multi-track Turing machine has a storage tape with several tracks; In other words, several symbols can be read per field, but only one read and write head. This write head always reads / writes all tracks of a field on the tape and then moves synchronously for all tracks (an essential difference to multiband Turing machines ). Otherwise, multi-track Turing machines behave just like classic Turing machines.

A multi-track Turing machine with only one belt corresponds exactly to the classic Turing machine and every multi-track Turing machine can be simulated by a classic Turing machine (with only one belt). The two machine models are therefore equivalent in terms of the predictability of functions, i.e. That is, both models can calculate the same functions.

Formal definition

Formally, a ( deterministic ) k-track Turing machine can be represented as a tuple . ${\displaystyle M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},\square ,F)}$

• ${\displaystyle Q}$ is the finite set of states.
• ${\displaystyle \Sigma }$is the finite input alphabet .
• ${\displaystyle \Gamma }$is the finite ribbon alphabet and it holds . ${\displaystyle \Sigma \subset \Gamma }$
• ${\displaystyle \delta \colon (Q\setminus F)\times \Gamma ^{k}\to Q\times \Gamma ^{k}\times \{L,N,R\}}$ is the (partial) transfer function.
• ${\displaystyle q_{0}\in Q}$ is the initial state.
• ${\displaystyle \square \in \Gamma \setminus \Sigma }$stands for the empty field (blank).
• ${\displaystyle F\subseteq Q}$ the set of final states.

The definition differs from that of a classic Turing machine (or a multi-band Turing machine) only in the definition of the transfer function. The partial transfer function supplies a state and the k tape symbols read from a field (i) the next state, (ii) k tape symbols that are written in the current field, and (iii) the direction of movement of the read / write head (L ... one space to the left, N… do not move, R… one space to the right). In contrast to the classic Turing machine, k symbols are read and written instead of just one symbol. It differs from the multi-band Turing machine in that it only defines one direction of movement for the read / write head, whereas in the case of multi-band Turing machines k defines movement directions (one for each read / write head). ${\displaystyle \delta }$ ${\displaystyle \delta }$ ${\displaystyle \delta }$

In order to define a nondeterministic variant of the k-track Turing machine, the transfer function is replaced by a transition relation : ${\displaystyle \delta }$

• ${\displaystyle \delta \subseteq (Q\setminus F)\times \Gamma ^{k}\times Q\times \Gamma ^{k}\times \{L,N,R\}}$

example

The following example is a 3-track Turing machine that adds 2 binary numbers of the same length. At the beginning the two given numbers are saved in the first two tracks and the output is saved in the third track. ${\displaystyle M=(\{q_{0},q_{1},q_{2},q_{f}\},\{0,1\},\{0,1,b\},\delta ,q_{0},b,\{q_{f}\})}$

We are gradually defining the transfer function. In state , the machine moves to the right end of the input. When the machine has left the state , the read / write head is on the last digit of the input. ${\displaystyle \delta }$ ${\displaystyle q_{0}}$ ${\displaystyle q_{0}}$

current state	read. symbol				schr. symbol			new condition	Head direction
${\displaystyle q_{0}}$	0	0	b	→	0	0	b	${\displaystyle q_{0}}$	R.
${\displaystyle q_{0}}$	0	1	b	→	0	1	b	${\displaystyle q_{0}}$	R.
${\displaystyle q_{0}}$	1	0	b	→	1	0	b	${\displaystyle q_{0}}$	R.
${\displaystyle q_{0}}$	1	1	b	→	1	1	b	${\displaystyle q_{0}}$	R.
${\displaystyle q_{0}}$	b	b	b	→	b	b	b	${\displaystyle q_{1}}$	L.

The two states and are used for the actual addition . Here corresponds to the addition at the current position without a carry bit from the previous step and the addition with a carry bit from the last step. Finally we define for and . ${\displaystyle q_{1}}$ ${\displaystyle q_{2}}$ ${\displaystyle q_{1}}$ ${\displaystyle q_{2}}$ ${\displaystyle \delta }$ ${\displaystyle q_{1}}$ ${\displaystyle q_{2}}$

current state	read. symbol				schr. symbol			new condition	Head direction
${\displaystyle q_{1}}$	0	0	b	→	0	0	0	${\displaystyle q_{1}}$	L.
${\displaystyle q_{1}}$	0	1	b	→	0	1	1	${\displaystyle q_{1}}$	L.
${\displaystyle q_{1}}$	1	0	b	→	1	0	1	${\displaystyle q_{1}}$	L.
${\displaystyle q_{1}}$	1	1	b	→	1	1	0	${\displaystyle q_{2}}$	L.
${\displaystyle q_{1}}$	b	b	b	→	b	b	b	${\displaystyle q_{f}}$	R.

current state	read. symbol				schr. symbol			new condition	Head direction
${\displaystyle q_{2}}$	0	0	b	→	0	0	1	${\displaystyle q_{1}}$	L.
${\displaystyle q_{2}}$	0	1	b	→	0	1	0	${\displaystyle q_{2}}$	L.
${\displaystyle q_{2}}$	1	0	b	→	1	0	0	${\displaystyle q_{2}}$	L.
${\displaystyle q_{2}}$	1	1	b	→	1	1	1	${\displaystyle q_{2}}$	L.
${\displaystyle q_{2}}$	b	b	b	→	b	b	1	${\displaystyle q_{f}}$	N

As an example we consider the addition of 0011 and 1010

step	Condition	Tape tracks
1	${\displaystyle q_{0}}$	b 0 011b
		b 1 010b
		b b bbbb
2	${\displaystyle q_{0}}$	b0 0 11b
		b1 0 10b
		bb b bbb
3	${\displaystyle q_{0}}$	b00 1 1b
		b10 1 0b
		bbb b bb
4th	${\displaystyle q_{0}}$	b001 1 b
		b101 0 b
		bbbb b b
5	${\displaystyle q_{0}}$	b0011 b
		b1010 b
		bbbbb b
6th	${\displaystyle q_{1}}$	b001 1 b
		b101 0 b
		bbbb b b

step	Condition	Tape tracks
7th	${\displaystyle q_{1}}$	b00 1 1b
		b10 1 0b
		bbb b 1b
8th	${\displaystyle q_{2}}$	b0 0 11b
		b1 0 10b
		bb b 01b
9	${\displaystyle q_{1}}$	b 0 011b
		b 1 010b
		b b 101b
10	${\displaystyle q_{1}}$	b 0011b
		b 1010b
		b 1101b
holds	${\displaystyle q_{f}}$	b 0 011b
		b 1 010b
		b 1 101b

Simulation by a classic Turing machine

Every k-track Turing machine can be simulated by a Turing machine . The states of the machine remain unchanged, but a larger band alphabet will have to be used for the classic Turing machine, which contains (1) all k-tuples over gamma and (2) the input alphabet. The transfer function or transfer relation will actually be taken over unchanged, but must be expanded to. A symbol is treated like the k-tuple in the constructed Turing machine . The k-tuple, which only contains blank symbols, functions as the blank symbol of the Turing machine M. Formally this can be expressed as follows: ${\displaystyle M^{k}=(Q,\Sigma ,\Gamma ,\delta ,q_{0},\square ,F)}$ ${\displaystyle M=(Q,\Sigma ,\Gamma ',\delta ',q_{0},\square ^{k},F)}$ ${\displaystyle \Sigma }$ ${\displaystyle a\in \Sigma }$ ${\displaystyle (a,\square ,\dotsc ,\square )}$ ${\displaystyle (\square ,\square ,\dotsc ,\square ),}$

• ${\displaystyle \Gamma '=\Gamma ^{k}\cup \Sigma }$
• For true iff ${\displaystyle \gamma _{k}\in \Gamma ^{k}}$ ${\displaystyle (q,\gamma _{k},q',\gamma _{k},D)\in \delta '}$ ${\displaystyle (q,\gamma _{k},q',\gamma _{k},D)\in \delta .}$
• For true iff ${\displaystyle \sigma \in \Sigma }$ ${\displaystyle (q,\sigma ,q',\gamma _{k},D)\in \delta '}$ ${\displaystyle (q,(\sigma ,\square ,\dotsc ,\square ),q',\gamma _{k},D)\in \delta .}$

literature

• Ingo Wegener : Theoretical Computer Science . An algorithm-oriented introduction. BG Teubner, Stuttgart, ISBN 3-519-02123-4 , 2. Turing machines, Church's thesis and decidability.
• Thomas A. Sudkamp: Languages ​​and Machines . An Introduction to the Theory of Computer Science. Second ed. Addison-Wesley, 1998, ISBN 0-201-82136-2 , 9.4. Multitrack machines.