Proportional error reduction measures

Proportional reduction in error Dimensions ( proportional reduction in error ( PFR ) english proportionate reduction of error , in short: PRE , hence PRE-degree ) enter indirectly the strength of the relationship between two variables and to. ${\displaystyle X}$ ${\displaystyle Y}$

definition

Proportional measures of error reduction are defined as

${\displaystyle PRE={\frac {E_{1}-E_{2}}{E_{1}}}=1-{\frac {E_{2}}{E_{1}}}}$,

wherein the error in predicting the dependent variable without knowledge of the relationship and the error in predicting the dependent variable with knowledge of the relationship is with . ${\displaystyle E_{1}}$ ${\displaystyle Y}$ ${\displaystyle E_{2}}$ ${\displaystyle Y}$ ${\displaystyle X}$

As is true (because it is believed that the knowledge of the relationship is correct, so the prediction error increases when using the knowledge from ) followed . A value of one means that knowing the independent variable, the value of the dependent variable can be perfectly predicted. A value of zero means that knowing the independent variable does not result in any improvement in predicting the dependent variable. ${\displaystyle 0\leq E_{2}\leq E_{1}}$ ${\displaystyle 0\leq PRE\leq 1}$

The advantage is that all proportional error reduction measures can be interpreted in the same way regardless of the scale level . The coefficient of determination can therefore serve as a benchmark , since it is a proportional error reduction measure , or the following rule of thumb:

• ${\displaystyle PRE<0{,}1}$: No relationship,
• ${\displaystyle 0{,}1\leq PRE<0{,}3}$: Weak relationship,
• ${\displaystyle 0{,}3\leq PRE<0{,}5}$: Medium relationship and
• ${\displaystyle 0{,}5\leq PRE}$: Strong relationship.

The downside is that

• the direction of the relationship cannot be taken into account, since directions can only be specified for ordinal or metric variables and
• the size of the error reduction depends on how the prediction is made with knowledge of the context. A small value of the proportional error reduction measure does not mean that there is no connection between the variables.

Since one variable is dependent and the other is independent, a distinction is made between symmetrical and asymmetrical proportional error reduction measures:

Scale level of		Measure
independent variable X	dependent variable Y	Surname	comment
nominal	nominal	Goodman and Kruskals ${\displaystyle \lambda }$	There is a symmetrical and an asymmetrical dimension.
nominal	nominal	Goodman and Kruskals ${\displaystyle \tau }$	There is a symmetrical and an asymmetrical dimension.
nominal	nominal	Uncertainty coefficient or part U	There is a symmetrical and an asymmetrical dimension.
ordinal	ordinal	Goodman and Kruskals ${\displaystyle \gamma }$	There is only one symmetrical dimension.
nominal	metric	${\displaystyle \eta ^{2}}$	There is only one asymmetrical dimension.
metric	metric	Coefficient of determination ${\displaystyle R^{2}}$	There is only one symmetrical dimension.

Coefficient of determination

For the prediction with ignorance of the relationship between two scale variables and only values ​​of the dependent variable may be used. The simplest approach is to assume a constant value. This value should meet the optimality property, i.e. minimize the sum of the squared deviations . It follows that the arithmetic mean is so . Hence the prediction error is ignorant of the context ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Y}$ ${\displaystyle {\hat {y}}_{i}^{(1)}=c}$ ${\displaystyle c=\min _{\tilde {c}}\sum _{i=1}^{n}(y_{i}-{\tilde {c}})^{2}}$ ${\displaystyle c}$ ${\displaystyle c={\bar {y}}}$

${\displaystyle E_{1}=\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i}^{(1)})^{2}=\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}$.

For the prediction with knowledge of the relationship, we use linear regression : ${\displaystyle {\hat {y}}_{i}^{(2)}=b_{0}+b_{1}x_{i}}$

${\displaystyle E_{2}=\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i}^{(2)})^{2}=\sum _{i=1}^{n}(y_{i}-b_{0}-b_{1}x_{i})^{2}}$.

The coefficient of determination is then a proportional error reduction measure , since the following applies ${\displaystyle R^{2}}$

${\displaystyle R^{2}=1-{\frac {E_{2}}{E_{1}}}=1-{\frac {\displaystyle \sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i}^{(2)})^{2}}{\displaystyle \sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}.}$

If the roles of the dependent and independent variables are swapped, the result is the same value for . Therefore there is only one symmetrical dimension. ${\displaystyle R^{2}}$

Goodman and Kruskals λ and τ

Calculation by Goodman and Kruskals and for the variables “Subjective class classification of the respondent” and “Voting intention in the Bundestag election” of the ALLBUS data 2006. ${\displaystyle \lambda }$ ${\displaystyle \tau }$

Goodman and Kruskals λ

The prediction with ignorance of the relationship is the modal category of the dependent variable and the prediction error

${\displaystyle E_{1}=1-{\frac {h_{M}}{n}}}$

with the absolute frequency in the modal category and the number of observations. ${\displaystyle h_{M}}$ ${\displaystyle n}$

The prediction with knowledge of the relationship is the modal category of the dependent variable depending on the categories of the independent variable and the prediction error

${\displaystyle E_{2}=\sum _{j}{\frac {h_{\bullet ,j}}{n}}\left(1-{\frac {h_{M,j}}{h_{\bullet ,j}}}\right)}$

with the absolute frequency for the respective category of the independent variable and the absolute frequency of the modal category depending on the categories of the independent variable. ${\displaystyle h_{\bullet ,j}}$ ${\displaystyle h_{M,j}}$

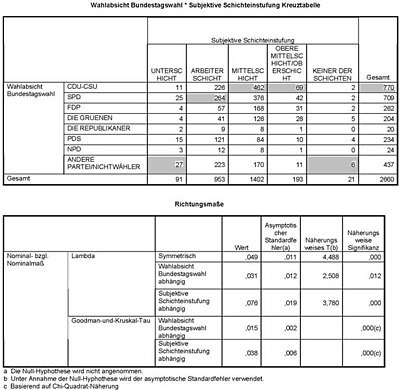
example

In the example on the right, the predictive value “CDU / CSU” and thus an error prediction results for the dependent variable “Intention to vote in the Bundestag election” if the correlation is not known . ${\displaystyle E_{1}=1-770/2660=0{,}711}$

Depending on the characteristics of the variable “Subjective class classification”, the predictive value “CDU / CSU” (category: middle class, upper middle class / upper class), “SPD” (category: working class) or “other party / Non-voters ”(all other categories). The prediction error and . ${\displaystyle {E_{2}=91/2660\cdot (1-27/91)+953/2660\cdot (1-264/953)+\dots +21/2660\cdot (1-6/21)=0{,}689}}$ ${\displaystyle \lambda =1-0{,}689/0{,}711=0{,}031}$

This means that in the present example, the error in predicting the respondent's intention to vote in the Bundestag election can be reduced by 3.1% if one knows one's own subjective class classification.

Goodman and Kruskals τ

In Goodman and Kruskals , a randomly drawn value from the distribution of Y is assumed as the predictive value instead of the modal category, i.e. H. with probability category 1 is drawn, with probability category 2 is drawn and so on. The prediction error then results as ${\displaystyle \tau }$ ${\displaystyle h_{1,\bullet }/n}$ ${\displaystyle h_{2,\bullet }/n}$

${\displaystyle E_{1}=\sum _{k}{\frac {h_{k,\bullet }}{n}}\left(1-{\frac {h_{k,\bullet }}{n}}\right)}$

with the absolute frequency of the category of the dependent variable. The prediction error results analogously , only that the prediction is now made accordingly for each category of the independent variable and the prediction error results as the sum of the weighted prediction errors in each category of the independent variable. ${\displaystyle h_{k,\bullet }}$ ${\displaystyle k}$ ${\displaystyle E_{2}}$ ${\displaystyle E_{2}}$

${\displaystyle E_{2}=\sum _{j}{\frac {h_{\bullet ,j}}{n}}\left(\sum _{k}{\frac {h_{k,j}}{h_{\bullet ,j}}}\left(1-{\frac {h_{k,j}}{h_{\bullet ,j}}}\right)\right)}$

with the absolute frequency for the common occurrence of the categories and . ${\displaystyle h_{k,j}}$ ${\displaystyle i}$ ${\displaystyle j}$

Symmetrical dimensions

For Goodman and Kruskals and can make forecast errors ${\displaystyle \lambda }$ ${\displaystyle \tau }$

• ${\displaystyle E_{1}^{Y}}$and , if the dependent variable is and ${\displaystyle E_{2}^{Y}}$ ${\displaystyle Y}$
• ${\displaystyle E_{1}^{X}}$and , if the dependent variable is, ${\displaystyle E_{2}^{X}}$ ${\displaystyle X}$

be calculated. The symmetrical measures for Goodman and Kruskals and then result as ${\displaystyle \lambda }$ ${\displaystyle \tau }$

${\displaystyle {\frac {(E_{1}^{X}-E_{2}^{X})+(E_{1}^{Y}-E_{2}^{Y})}{E_{1}^{X}+E_{1}^{Y}}}}$.

Uncertainty coefficient

entropy

The uncertainty coefficient measures the uncertainty of the information with the help of entropy . If the relative frequency of occurrence is the category , then the entropy or uncertainty is defined as ${\displaystyle f_{k}}$ ${\displaystyle k}$

${\displaystyle U=-\sum _{k}f_{k}\,\log(f_{k}).}$

Uncertainty is zero if there is but one for all possible categories . Predicting which category value a variable will take on is then trivial. If ( equal distribution ), then the uncertainty and also maximum. ${\displaystyle U}$ ${\displaystyle f_{k}=0}$ ${\displaystyle f_{k}=1/k}$ ${\displaystyle U=\log(k)}$

Asymmetric uncertainty coefficient

The measure of error with ignorance of the relationship is therefore the uncertainty for the dependent variable ${\displaystyle U_{Y}}$

${\displaystyle E_{1}=-\sum _{k}{\frac {h_{k,\bullet }}{n}}\log \left({\frac {h_{k,\bullet }}{n}}\right)=U_{Y}.}$

The measure of error with knowledge of the relationship is the weighted sum of the uncertainty for each category of the dependent variable

${\displaystyle E_{2}=\sum _{j}{\frac {h_{\bullet ,j}}{n}}\underbrace {\left[-\sum _{k}{\frac {h_{k,j}}{h_{\bullet ,j}}}\log \left({\frac {h_{k,j}}{h_{\bullet ,j}}}\right)\right]} _{\begin{matrix}{\text{Unsicherheit in Kategorie }}j\\{\text{der unabhängigen Variable}}\end{matrix}}.}$

This expression can also be written as

${\displaystyle E_{2}=U_{XY}-U_{X}=\left[-\sum _{j,k}{\frac {h_{k,j}}{n}}\log \left({\frac {h_{k,j}}{n}}\right)\right]-\left[-\sum _{j}{\frac {h_{\bullet ,j}}{n}}\log \left({\frac {h_{\bullet ,j}}{n}}\right)\right]}$

with the uncertainty based on the joint distribution of and and the uncertainty of the independent variable . ${\displaystyle U_{XY}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle U_{X}}$ ${\displaystyle X}$

The uncertainty coefficient then results as

${\displaystyle U_{\text{asym.}}={\frac {E_{1}-E_{2}}{E_{1}}}={\frac {U_{X}+U_{Y}-U_{XY}}{U_{Y}}}.}$

Symmetrical uncertainty coefficient

For the uncertainty coefficient, the prediction errors

• ${\displaystyle E_{1}^{Y}}$and , if the dependent variable is and ${\displaystyle E_{2}^{Y}}$ ${\displaystyle Y}$
• ${\displaystyle E_{1}^{X}}$and , if the dependent variable is, ${\displaystyle E_{2}^{X}}$ ${\displaystyle X}$

be calculated. The symmetrical uncertainty coefficient results, as in Goodman and Kruskals and , als ${\displaystyle \lambda }$ ${\displaystyle \tau }$

${\displaystyle U_{\text{sym.}}={\frac {(E_{1}^{X}-E_{2}^{X})+(E_{1}^{Y}-E_{2}^{Y})}{E_{1}^{X}+E_{1}^{Y}}}={\frac {2(U_{X}+U_{Y}-U_{XY})}{U_{X}+U_{Y}}}}$.

Goodman and Kruskals γ

${\displaystyle C}$be the number of concordant pairs ( and ) and the number of discordant pairs ( and ). If we don't have ties in common and the number of observations is, then . ${\displaystyle x_{i}<x_{j}}$ ${\displaystyle y_{i}<y_{j}}$ ${\displaystyle D}$ ${\displaystyle x_{i}<x_{j}}$ ${\displaystyle y_{i}>y_{j}}$ ${\displaystyle n}$ ${\displaystyle C+D=n(n-1)/2}$

Under ignorance of the context, we can not comment on whether a couple is concordant or discordant. Therefore we predict probability 0.5 of a concordant or discordant pair. The total error for all possible pairs is given as

${\displaystyle E_{1}={\frac {C+D}{2}}.}$

Under knowledge of the relationship concordance will always be predicted, if , or more discordance when . The mistake is ${\displaystyle C\geq D}$ ${\displaystyle C<D}$

${\displaystyle E_{2}=\min(C,D)=\left\{{\begin{matrix}D,&{\text{ falls }}C\geq D\\C,&{\text{ falls }}C<D\end{matrix}}\right.}$

and it follows

${\displaystyle {\frac {E_{1}-E_{2}}{E_{1}}}={\frac {{\frac {C+D}{2}}-\min(C,D)}{\frac {C+D}{2}}}={\frac {|C-D|}{C+D}}=|\gamma |.}$

The Goodman and Kruskals amount is thus a symmetrical, proportional error reduction measure. ${\displaystyle \gamma }$

η ²

Calculation of the variables “net income of respondent” (dependent) and “subjective class classification of respondent” (independent) of the ALLBUS data 2006. ${\displaystyle \eta }$

As with the coefficient of determination , the predictive value for the dependent scale variable is ignorant of the context and the prediction error ${\displaystyle {\bar {y}}}$

${\displaystyle E_{1}=\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}$.

If it is known to which of the groups of the nominal or ordinal independent variable the observation belongs, the predictive value is precisely the group mean . The prediction error results as ${\displaystyle {\bar {y}}_{k}}$

${\displaystyle E_{2}=\sum _{k}\sum _{i=1}^{n}(y_{i}-{\bar {y}}_{k})^{2}\delta _{ik}}$

with if the observation belongs to the group and otherwise zero. This results in ${\displaystyle \delta _{ik}=\left\{{\begin{matrix}1,&{\text{ falls }}i=k\\0&{\text{ sonst }}\end{matrix}}\right.}$ ${\displaystyle i}$ ${\displaystyle k}$

${\displaystyle \eta ^{2}=1-{\frac {E_{2}}{E_{1}}}=1-{\frac {\sum _{k}\sum _{i=1}^{n}(y_{i}-{\bar {y}}_{k})^{2}\delta _{ik}}{\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}$.

The roles of the dependent and independent variables cannot be reversed because they have different scale levels. Therefore there is only one (asymmetrical) dimension.

Cohen (1998) gives as a rule of thumb:

• ${\displaystyle \eta ^{2}<0{,}01}$ no context,
• ${\displaystyle 0{,}01\leq \eta ^{2}<0{,}04}$ little connection,
• ${\displaystyle 0{,}04\leq \eta ^{2}<0{,}16}$ medium relationship and
• ${\displaystyle 0{,}16\leq \eta ^{2}}$ strong connection.

example

In the example, the error in the prediction of the net income can be reduced by just under 10% if the social class is known. The second comes about if you swap the role of the variables, which is nonsensical here. Therefore this value must be ignored. ${\displaystyle 0{,}306^{2}=0{,}094}$ ${\displaystyle \eta }$

literature

• YMM Bishop, SE Feinberg, PW Holland (1975). Discrete Multivariate Analysis: Theory and Practice. Cambridge, MA: MIT Press.
• LC Freemann (1986). Order-based Statistics and Monotonicity: A Family of Ordinal Measures of Association. Journal of Mathematical Sociology, 12 (1), pp. 49-68
• J. Bortz (2005). Statistics for human and social scientists (6th edition), Springer Verlag.
• B. Rönz (2001). Script "Computer-assisted Statistics II", Humboldt University Berlin, Chair for Statistics.

Individual evidence

1. ↑ ^{a b} J. Cohen (1988). Statistical Power Analysis for Behavioral Science. Erlbaum, Hilsdale.
2. ↑ ^{a b c} L.A. Goodman, WH Kruskal (1954). Measures of association for cross-classification. Journal of the American Statistical Association, 49, pp. 732-764.
3. ^ H. Theil (1972), Statistical Decomposition Analysis, Amsterdam: North-Holland Publishing Company (discusses the uncertainty coefficient).