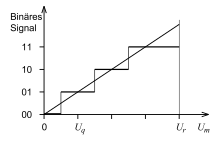
Quantization characteristic
The quantization curve graphically describes the relationship between the input signal (e.g. an infinitely variable electrical voltage) and the output signal of a quantizer . Their course is step-shaped.
The measuring range of the input signal is divided into intervals. The quantization level is the output value onto which all values from an interval are mapped.
Linear quantization
A linear quantization curve has steps of the same width over the entire display area; in the limit of extremely small steps it appears as a straight line. Such characteristics are used in measurement technology and in telecommunications for high-quality signals, such as E.g .: audio CD format (16 bit), ADAT (16 bit), AES / EBU (16, 20 or 24 bit). The less a signal uses a given range of values ( measuring range ), the more clearly the gradation becomes noticeable as a relative quantization deviation or quantization noise . Since the resolution of the audio sources mentioned is high from the start, compression (also called companding) in the "quieter" areas, i.e. the areas with lower voltage, is not necessary and also only possible with great difficulty.
Nonlinear quantization
A non-linear quantization curve has a finer gradation within its value range for smaller signals. Such characteristics are used for audio and video signals in order to compress them. The human ear perceives the gradation with quiet signals to a lesser extent than with a linear characteristic. A logarithmic quantization aims for a signal-to-noise ratio (SNR) that is constant over a wide dynamic range of an audio signal.
The quantization characteristics of the A-law and µ-law method are used in PCM technology in digital telephone networks.
Digital video technology also uses non-linear quantization characteristics. In poorly detailed and calm areas of the image, several pixels can be combined to form so-called macro blocks.
Quantization levels
Number and width
The number of steps with which the analog signal is quantized determines the resolution of the quantization. Representation by binary digits creates levels. With a linear characteristic, an interval can be set from 0 to in steps of width
subdivide. The picture explains this in a rough resolution , there are four levels:
| horizontal | vertical binary |
vertical decimal |
|---|---|---|
| 0… ¼ | 00 | 0 |
| ¼ … ½ | 01 | 1 |
| ½ … ¾ | 10 | 2 |
| ¾ ... | 11 | 3 |
- Note: In digital technology, it is common not to number from 1, but from 0.
An 8-bit resolution, as it is common in telephone networks and, to a large extent, also in the digitization of video signals, generates 256 quantization levels (with the values 0 ... 255). (In video technology, the values 0 and 255 are left out: They are used to generate the sync signals ). The level range of the analog signal that can be achieved in this way is referred to as system dynamics. Logarithmic characteristics increase the system dynamics.
The relative resolution is calculated using the width of the steps. The signal-to-noise ratio SNR results from
- SNR = 6.02 dB + 1.76 dB.
The following value is obtained for a linear gradation:
| Number of digits |
Number of stages |
Relative resolution |
SNR |
|---|---|---|---|
| 8 bit | 256 | 3.9 mV / V | 50 dB |
| 16 bit | 65536 | 15.3 µV / V | 98 dB |
| 24 bit | 16777216 | 60 nV / V | 146 dB |
If the signal range is only used to 10%, the SNR drops by 20 dB.
Reference to inconsistent presentation
- example 1
The voltage range 0 ... 10 V is represented by 2 bits in linear assignment to the possible 4 values:
a) Representation to be found in the literature: The smallest binary value belongs to the smallest voltage, the largest binary value to the highest voltage.
00 ↔ 0 V; 01 ↔ 3.3 V; 10 ↔ 6.7 V; 11 ↔ 10 V
The drawing at the top left belongs to this illustration.
A further 4 binary values may be added to these 4 binary values with a correspondingly larger voltage range and larger value set 000 ... 111.
Those who advocate the above point of view may please continue the drawing.
b) Representation used above: Each quantization level has a step size, including the last. The voltage range goes from the left edge of the first step to the right edge of the last step according to the table above:
00 ↔ 0 ... 2.5 V; 01 ↔ 2.5 ... 5 V; 10 ↔ 5 ... 7.5 V; 11 ↔ 7.5 ... 10 V
The drawing at the bottom left belongs to this illustration.
The addition of the 4 binary values is possible with continuous steps of the same height and steps of the same width, which now reach up to 20 V, see drawing below right.
- Example 2
This is a non-binary, but digital example: A station clock lets its minute hand advance by one step every minute with the possible values 00 ... 59. For a cycle of one hour: Depending on the representation, 59 or 60 steps would have to be required.
Bipolar input voltage
The characteristic curves shown so far apply to a unipolar voltage range . For a bipolar voltage range , the step-like curve should continue without a break at the zero point. There are two options called “midtread” and “midrise”, see picture.
In practice, midrise quantizers show a slight noise when there is no input signal or the input signal is zero, as the thermal noise causes the quantization level to jump back and forth above and below zero. A midtread quantizer provides here, e.g. B. in pauses in speech, a noise-free ("silent") signal.
Individual evidence
- ↑ Ke-Lin Du, MNS Swamy: Wireless Communication Systems: From RF Subsystems to 4G Enabling Technologies. Cambridge University Press, 2010, p. 471.
- ^ Marina Bosi, Richard E. Goldberg: Introduction to Digital Audio Coding and Standards. Springer, 2003, p. 22 ff.
- ^ Josef Hoffmann, Franz Quint: Signal processing with MATLAB and Simulink: Application-oriented simulations. Oldenbourg, 2012, p. 134.