Split operator method

The split operator method (SOP) is a numerical method with which the time-dependent Schrödinger equation can be solved. In the method, the Hamilton operator is split into a kinetic part (momentum part) and a potential part and used individually. The fast Fourier transform (FFT) is used to distinguish between momentum space and spatial space. ${\displaystyle {\hat {H}}}$ ${\displaystyle {\hat {T}}}$ ${\displaystyle {\hat {V}}}$

The Schrödinger equation

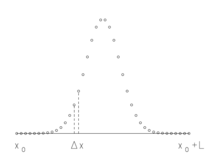
The wave function shown on an equidistant grid (spatial space) ${\displaystyle \psi (x)}$

The wave function shown on an equidistant grid (momentum space) ${\displaystyle \psi (k)}$

The time-dependent Schrödinger equation is defined as

${\displaystyle i\hbar {\frac {\partial \psi (x,t)}{\partial t}}={\hat {H}}(t)\psi (x,t),}$

where is the Hamilton operator. ${\displaystyle \textstyle {\hat {H}}(t)=-{\frac {\hbar ^{2}}{2m}}\Delta +V(t)}$

The wave function is shown in spatial space on an equidistant grid. The values ​​from currently at the grid points are specified as starting values . The method calculates the wave function at a later point in time. ${\displaystyle \psi (x,t)}$ ${\displaystyle \psi (x,t_{0})}$ ${\displaystyle t_{0}}$ ${\displaystyle t=t_{0}+\Delta t}$

The effect of the Hamilton operator on a wave function is calculated using the fast Fourier transform. In addition to the grid in the local space, a grid in the momentum space is also required. The resolution in momentum space is determined by the length of the grid in spatial space. It applies where is the number of grid points. ${\displaystyle \textstyle {\hat {H}}(t)={\frac {{\hat {\mathbf {p} }}^{2}}{2m}}+{\hat {V}}(t)}$ ${\displaystyle {\hat {H}}\psi ={\hat {T}}\psi +{\hat {V}}\psi }$ ${\displaystyle \Delta k={\tfrac {2\pi }{L}}}$ ${\displaystyle L}$ ${\displaystyle \Delta k\Delta x={\tfrac {2\pi }{N}}}$ ${\displaystyle N}$

Application of the discrete Fourier transform

The potential operator has a diagonal matrix representation in spatial space and therefore acts locally on every grid point : ${\displaystyle {\hat {V}}}$ ${\displaystyle x_{i}}$

${\displaystyle \left({\hat {V}}(t)\psi \right)(x_{i})=V(x_{i},t)\cdot \psi (x_{i}).}$

The kinetic operator is calculated in the same way with its diagonal representation in momentum space. The following applies to each grid point : ${\displaystyle {\hat {T}}}$ ${\displaystyle k_{i}}$

${\displaystyle \left({\hat {T}}{\tilde {\psi }}\right)(k_{i}))={\frac {\hbar ^{2}}{2m}}{k_{i}}^{2}{\tilde {\psi }}(k_{i}).}$

The discrete representation of the wave function in the momentum space is given by the discrete Fourier transformation : ${\displaystyle {\tilde {\psi }}(k_{i})}$ ${\displaystyle {\hat {Z}}^{\dagger }}$

${\displaystyle {\tilde {\psi }}(k_{i})=\langle k_{i}|\psi \rangle =\sum _{x_{j}}\langle k_{i}|x_{j}\rangle \langle x_{j}|\psi \rangle ={\frac {\Delta x}{\sqrt {2\pi }}}\sum _{x_{j}}e^{-ik_{i}x_{j}}\psi (x_{j})}$

In vector notation, this equation is

${\displaystyle {\vec {\tilde {\psi }}}=c^{-1}{\hat {Z}}^{\dagger }{\vec {\psi }}}$

With

${\displaystyle {\vec {\tilde {\psi }}}:=({\tilde {\psi }}(k_{0}),\dotsm ,{\tilde {\psi }}(k_{N-1}))^{T}}$

${\displaystyle {\vec {\psi }}:=(\psi (x_{0}),\dotsm ,\psi (x_{N-1}))^{T}}$

${\displaystyle Z_{ij}:=N^{-{\frac {1}{2}}}e^{+ik_{i}x_{j}}}$

${\displaystyle c:={\tfrac {\sqrt {2\pi N}}{L}}.}$

Correspondingly, one obtains for the back transformation into the spatial space

${\displaystyle \psi (x_{j})={\frac {\Delta k}{\sqrt {2\pi }}}\sum _{k_{i}}e^{+ik_{i}x_{j}}{\tilde {\psi }}(k_{i})}$

respectively

${\displaystyle {\vec {\psi }}=c{\hat {Z}}{\vec {\tilde {\psi }}}}$

with the grid steps or . Here is the length of the grid in spatial space and the number of points in spatial and momentum space. The constant is only required if the correct normalization of the function is required. The Fourier transform receives the norm of the vectors and . ${\displaystyle \Delta x={\tfrac {L}{N}}}$ ${\displaystyle \Delta k={\tfrac {2\pi }{L}}}$ ${\displaystyle L}$ ${\displaystyle N}$ ${\displaystyle c}$ ${\displaystyle {\tilde {\psi }}}$ ${\displaystyle {\vec {\tilde {\psi }}}}$ ${\displaystyle {\vec {\psi }}}$

Split operator method

The calculation of the function of an operator is particularly easy in the diagonal representation of the operator. The split operator method uses a decomposition of the Hamilton operator into the operators for kinetic energy and for potential energy , which assume diagonal form in momentum or spatial space. ${\displaystyle e}$ ${\displaystyle {\hat {T}}}$ ${\displaystyle {\hat {V}}}$

The error resulting from the non-interchangeability of and can be caused by the symmetrical split ${\displaystyle {\hat {T}}}$ ${\displaystyle {\hat {V}}}$

${\displaystyle e^{-{\frac {i}{\hbar }}{\hat {H}}\Delta t}\approx e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}\cdot e^{-{\frac {i}{\hbar }}{\hat {V}}\Delta t}\cdot e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}}$

can be reduced to terms of the order of magnitude : With and one obtains for the right side ${\displaystyle {\Delta t}^{3}}$ ${\displaystyle {\hat {X}}:=-{\tfrac {i}{\hbar }}{\hat {T}}\Delta t}$ ${\displaystyle {\hat {Y}}:=-{\tfrac {i}{\hbar }}{\hat {V}}\Delta t}$

${\displaystyle \exp \left({\frac {\hat {X}}{2}}\right)\exp \left({\hat {Y}}\right)\exp \left({\frac {\hat {X}}{2}}\right)=\exp \left({\frac {\hat {X}}{2}}+{\hat {Y}}+{\frac {\hat {X}}{2}}+\underbrace {{\frac {1}{2}}\left[{\frac {\hat {X}}{2}},{\hat {Y}}\right]+{\frac {1}{2}}\left[{\hat {Y}},{\frac {\hat {X}}{2}}\right]} _{0}+{\frac {1}{12}}\left[\left[{\frac {\hat {X}}{2}},{\hat {Y}}\right],{\hat {X}}+2{\hat {Y}}\right]+\dotsm \right).}$

The leading error term is therefore proportional to . ${\displaystyle {\Delta t}^{3}\left[\left[{\hat {T}},{\hat {V}}\right],{\hat {T}}+2{\hat {V}}\right]}$

Diagonal shape

A coordinate transformation from position space to momentum space enables simple calculation of ${\displaystyle {\hat {Z}}^{\dagger }}$

${\displaystyle e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}\psi ={\hat {Z}}e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}{\hat {Z}}^{\dagger }\psi .}$

With the diagonal representation of the operator of kinetic energy

${\displaystyle {\hat {T}}={\hat {Z}}^{\dagger }{\hat {T}}{\hat {Z}}={\begin{pmatrix}{\frac {\hbar ^{2}}{2m}}{k_{0}}^{2}&0&\cdots &0\\0&\ddots &0&0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &{\frac {\hbar ^{2}}{2m}}k_{N-1}^{2}\\\end{pmatrix}}}$

you get

${\displaystyle e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}={\begin{pmatrix}\ddots &0&\cdots &0\\0&e^{-{\frac {i}{\hbar }}{\frac {\Delta t}{2}}{\frac {\hbar ^{2}}{2m}}k_{i}^{2}}&0&0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &\ddots \\\end{pmatrix}}.}$

The coordinate transformation takes place on the -point grid with the help of the discrete Fourier transformation: ${\displaystyle N}$ ${\displaystyle x_{0},\dotsm ,x_{N-1}}$

${\displaystyle {\tilde {\psi }}(k_{i})=N^{-{\frac {1}{2}}}\sum _{j=0}^{N-1}\psi (x_{j})e^{-ik_{i}x_{j}}}$     For   ${\displaystyle i=0,\dotsm ,N-1}$

or . ${\displaystyle {\vec {\tilde {\psi }}}={\hat {Z}}^{\dagger }{\vec {\psi }}}$

Numerical algorithm

See also : algorithm

By combining the successive terms of two time steps, the number of Fourier transforms, i.e. H. the numerical effort, reduce :, and the two functions with result . ${\displaystyle {\hat {Z}}e^{-{\frac {i}{\hbar }}{\frac {\hat {T}}{2}}\Delta t}{\hat {Z}}^{\dagger }}$ ${\displaystyle {\hat {Z}}^{\dagger }{\hat {Z}}=1}$ ${\displaystyle e}$ ${\displaystyle {\frac {\hat {T}}{2}}}$ ${\displaystyle e^{-{\frac {i}{\hbar }}{\hat {T}}\Delta t}}$

The wave function according to time steps is thus obtained by: ${\displaystyle n}$

• Fourier transform of ${\displaystyle \psi _{0}}$
• Multiplication by the diagonal elements (half time step) ${\displaystyle e^{-{\frac {i}{\hbar }}{\frac {\Delta t}{2}}{\frac {\hbar ^{2}}{2m}}k_{i}^{2}}}$
• Inverse transformation
• Multiplication by the diagonal elements ${\displaystyle e^{-{\frac {i}{\hbar }}V_{i}\Delta t}}$
• Fourier transform
• Multiplication by the diagonal elements (whole time step) ${\displaystyle e^{-{\frac {i}{\hbar }}\Delta t{\frac {\hbar ^{2}}{2m}}k_{i}^{2}}}$
• etc., until the last step requires another multiplication by half the time step as in the second line.

literature

• IN Bronstein, KA Semendjajew, G. Musiol, H. Muehlig: Taschenbuch der Mathematik. German Harri GmbH, 2008.
• T. Fließbach: Quantum Mechanics: Textbook on Theoretical Physics III. 5th edition, Spektrum Akademischer Verlag, 2008, ISBN 978-3-8274-2020-6 .
• Herbert Sager: Fourier Transformation. vdf Hochschulverlag, Zurich 2012, ISBN 978-3-7281-3393-9 .
• A. Askar, AS Cakmak: Explicit integration method for the time-dependent Schrodinger equation for collision problems . In: Journal of Chemical Physics . tape 68 , no. 6 , 1978, p. 2794-2798 , doi : 10.1063 / 1.436072 .
• JB Delos: Theory of Electronic Transitions in Slow Atomic Collisions . In: Physical Review . tape 176 , no. 1 , 1968, p. 141-150 , doi : 10.1103 / PhysRev.176.141 .
• Juha Javanainen, Janne Ruostekoski: Symbolic calculation in development of algorithms: split-step methods for the Gross – Pitaevskii equation . In: Journal of Physics A . tape 39 , 2006, p. L179 – L184 , doi : 10.1088 / 0305-4470 / 39/12 / L0 .
• Michael Hintenender: Propagation of wave packets . In: MPQ reports . MPQ163. Garching 1992 ( online ).