Stationary distribution

An invariant distribution or a stationary distribution is a term from the theory of Markov chains ; these in turn are special stochastic processes and thus objects of investigation of stochastics .

A Markov chain has a stationary distribution if and only if there is a starting distribution that does not change over time.

Stationary distributions are not to be confused with the stationarity of a stochastic process or stationary transition probabilities .

definition

Given is a homogeneous Markov chain in discrete time with at most a countable state space . Then a distribution on stationary distribution is called if ${\displaystyle (X_{n})_{n\in \mathbb {N} }}$ ${\displaystyle Z}$ ${\displaystyle P_{\pi }}$ ${\displaystyle Z}$

${\displaystyle P_{\pi }(\{j\})=\sum _{i\in Z}P_{\pi }(\{i\})p(i,j)}$

holds for all , where is the transition probability from state to state (which is independent of the point in time ). In the case of a finite state space, this corresponds ${\displaystyle j\in Z}$ ${\displaystyle p(i,j)=P(X_{n}=j|X_{n-1}=i)}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle n}$

${\displaystyle \pi M=\pi }$,

where is the transition matrix and a probability vector is written as a row vector. In this case, the stationary distributions are precisely the left eigenvectors of the transition matrix for eigenvalue 1, which were normalized with respect to the sum norm . ${\displaystyle M}$ ${\displaystyle \pi }$

Existence and uniqueness

In general, stationary distributions do not have to exist. An example of this are transient Markov chains . These never have stationary distributions. Conversely, it can also be shown that irreducible Markov chains have at most a stationary distribution. The following statements apply to the uniqueness of the stationary distributions:

• An irreducible Markov chain has a stationary distribution if and only if it is positive recurrent . The distribution is then given by

${\displaystyle P_{\pi }(\{i\})={\frac {1}{\operatorname {E} (\tau _{ii})}}}$.

Here, the return period in the state , if started in this. ${\displaystyle \tau _{ii}}$ ${\displaystyle i}$

• In the case of a finite state space, the irreducibility of the Markov chain and the irreducibility of the transition matrix are equivalent. From this it follows immediately with Perron-Frobenius' theorem that a clear invariant distribution (or left-hand eigenvector) exists and thus that the Markov chain is positive-recurrent. Thus positive recurrence follows from irreducibility.
• Accordingly, an irreducible Markov chain with finite state space always has a stationary distribution. This corresponds exactly to the normalized left eigenvector for eigenvalue 1 of the transition matrix or the standardized eigenvector of the transposed transition matrix for eigenvalue 1. ${\displaystyle M}$ ${\displaystyle M^{T}}$
• If a distribution satisfies the detailed balance equation , then this distribution is a stationary distribution.

convergence

An irreducible, positively recurrent Markov chain converges to a stationary distribution if and only if it is aperiodic. Convergence here means that

${\displaystyle \lim _{n\to \infty }P(X_{n}=i)=P_{\pi }(\{i\})}$

holds for every start distribution of and every state . ${\displaystyle X_{0}}$ ${\displaystyle i\in Z}$

If the state space is finite, then the lines of converge towards the stationary distribution. ${\displaystyle M^{n}}$

At finite state spaces often finds the convergence criteria that must exist so that the transition matrix applies that is. This corresponds to checking the matrix for aperiodicity and irreducibility. ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle M}$ ${\displaystyle M^{k}>0}$

If the aperiodicity is dispensed with, the following statement can be made: If a Markov chain is irreducible and recurrent, then

${\displaystyle \lim _{N\to \infty }{\frac {1}{N}}\sum _{n=0}^{N-1}P(X_{n}=i)={\frac {1}{\operatorname {E} (\tau _{ii})}}=P_{\pi }(\{i\})}$.

The mean value of the probability of occurrence thus converges component-wise to the stationary distribution.

More generally, if the Markov chain is not irreducible, it breaks down into several subsets of states that communicate with each other and all have the same period . Is such a set with an arbitrary but fixed state from this set. Then each state can be reached from this set in a clear number of steps from. If the subset is now recurrent, then the following applies ${\displaystyle d}$ ${\displaystyle K(i)}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle k}$ ${\displaystyle i}$ ${\displaystyle T(i)}$

${\displaystyle \lim _{n\to \infty }p_{ij}^{nd+k}={\frac {d}{\operatorname {E} (\tau _{jj})}}}$.

Convergence speed

For some applications it is particularly interesting how quickly the stationary distribution is achieved. It can be shown that if for holds and all eigenvalues ​​are simple, then the following estimate holds: ${\displaystyle 1=\lambda _{1}>|\lambda _{2}|\geq |\lambda _{3}|\dots }$ ${\displaystyle M}$

${\displaystyle \Vert v_{0}M^{n}-P_{\pi }\Vert \leq C|\lambda _{2}|^{n}}$

For any start distribution . The most important influencing factor on the speed of convergence is therefore the second largest eigenvalue in terms of absolute value. ${\displaystyle v_{0}}$

Comparable statements can still be made for weaker prerequisites for the transition matrix, but correction terms for the Jordan blocks must be introduced.

Examples

Finite state space

existence

Let us consider the Markov chain with the following transition matrix:

${\displaystyle M={\begin{bmatrix}1&0&0&0&0\\0{,}1&0&0{,}8&0{,}1&0\\0&0{,}5&0&0&0{,}5\\0&0&0&0&1\\0&0&0&1&0\end{bmatrix}}}$

This Markov chain has two absorbing quantities : and . Since these states can no longer be left, they have an influence on the existence of the stationary distributions. This can also be seen in the normalized eigenvectors. These are and . The stationary distribution is therefore not unambiguous here. ${\displaystyle A=\{1\}}$ ${\displaystyle B=\{4,5\}}$ ${\displaystyle \pi _{1}=(1,0,0,0,0)}$ ${\displaystyle \pi _{2}=(0,0,0,0{,}5,0{,}5)}$

Uniqueness

The examined Markov chain

Let us consider the Markov chain with the transition graph shown on the right. For the sake of simplicity, we set all transition probabilities to 0.5. The Markov chain is irreducible, as one can move from any state to any other state in a maximum of two steps. But it is also periodic, since a return to the starting point is only possible at even times. The also irreducible transition matrix is then

${\displaystyle M={\begin{bmatrix}0&0{,}5&0&0{,}5\\0{,}5&0&0{,}5&0\\0&0{,}5&0&0{,}5\\0{,}5&0&0{,}5&0\end{bmatrix}}}$

Perron-Frobenius' theorem guarantees the uniqueness of the eigenvector, since the matrix is ​​also double-stochastic , it has the stationary distribution . However, the matrix powers do not converge, in particular is and ${\displaystyle \pi ={\frac {1}{4}}(1,1,1,1)}$ ${\displaystyle M^{2n+1}=M}$

${\displaystyle M^{2n}=M^{2}={\begin{bmatrix}0{,}5&0&0{,}5&0\\0&0{,}5&0&0{,}5\\0{,}5&0&0{,}5&0\\0&0{,}5&0&0{,}5\end{bmatrix}}}$

But if we now consider the mean values, they converge to the corresponding component of the stationary distribution:

${\displaystyle \lim _{N\to \infty }{\frac {1}{N}}\sum _{n=0}^{N-1}P(X_{n}=1|X_{0}=1)=\lim _{N\to \infty }{\frac {1}{N}}\sum _{n=0}^{N-1}p_{11}^{n}\rightarrow {\frac {1}{4}}{\text{ für }}N\to \infty }$.

This follows the transition matrix above with the help of the corresponding entries (in the example the first row and column).

convergence

A simple Markov chain

Consider the Markov chain shown on the right with the transition probabilities as given in the transition matrix:

${\displaystyle M={\begin{bmatrix}0{,}5&0&0{,}5\\0{,}1&0{,}5&0{,}4\\0&0{,}5&0{,}5\end{bmatrix}}}$

It then applies

${\displaystyle M^{2}={\frac {1}{100}}{\begin{bmatrix}25&25&50\\10&45&45\\5&50&45\end{bmatrix}}>0}$

Thus the Markov chain is irreducible (and thus also positively recurrent), aperiodic and accordingly converges to a stationary distribution. An eigenvector of to the eigenvalue 1 is , normalization to 1 with respect to the sum norm delivers as a unique invariant distribution ${\displaystyle M^{T}}$ ${\displaystyle v=(1,5,5)}$

${\displaystyle \pi ={\frac {1}{11}}(1,5,5)=(0.0909,0.4545,0.4545)}$.

If you calculate the matrix powers, then if two decimal places already match the exact solution, if there are more than four decimal places. Conversely, from the stationary distribution calculated as the left eigenvector, one can immediately specify the limit value of the matrix powers in the event of convergence, since these converge line by line to the stationary distribution: ${\displaystyle M^{6}}$ ${\displaystyle M^{12}}$

${\displaystyle \lim _{n\to \infty }M^{n}={\frac {1}{11}}\cdot {\begin{bmatrix}1&5&5\\1&5&5\\1&5&5\end{bmatrix}}}$

The expected return time can also be calculated from the stationary distribution; this is exactly the reciprocal of the corresponding component of the distribution. So here is the average time from starting in 1 to returning

${\displaystyle \operatorname {E} (\tau _{11})={\frac {1}{\pi _{1}}}=11}$.

Variant of the random walk

Transition graph with transition probabilities exemplarily for states 1, 5, 6 and 8. There is a secret passage between states 2 and 8 for both directions.

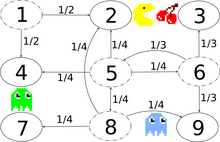
The game character Pac-Man eats small balls and cherries in a maze and is followed by ghosts. For the sake of simplicity, the game world in this example is a small grid and the monsters move purely at random. Every horizontally and vertically adjacent playing field is the next location of the ghost with the same probability, with the exception of a secret passage between the states and (see transition graphs on the right). ${\displaystyle 3\times 3}$ ${\displaystyle 2}$ ${\displaystyle 8}$

The state space is { }. In the transition matrix that now follows , entries have probably been removed in order to obtain a better overview: ${\displaystyle Z=}$ ${\displaystyle 1,2,3,4,5,6,7,8,9}$ ${\displaystyle P}$ ${\displaystyle 0}$

${\displaystyle P={\begin{pmatrix}&{\frac {1}{2}}&&{\frac {1}{2}}\\{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}&&&{\frac {1}{4}}\\&{\frac {1}{2}}&&&&{\frac {1}{2}}\\{\frac {1}{3}}&&&&{\frac {1}{3}}&&{\frac {1}{3}}\\&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}\\&&{\frac {1}{3}}&&{\frac {1}{3}}&&&&{\frac {1}{3}}\\&&&{\frac {1}{2}}&&&&{\frac {1}{2}}\\&{\frac {1}{4}}&&&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}\\&&&&&{\frac {1}{2}}&&{\frac {1}{2}}\end{pmatrix}}}$

This Markov chain is irreducible because the ghosts can move from any state to any state in a finite time. Thanks to the secret passage, only a maximum of three status changes are necessary. Through the secret passage, the Markov chain is also aperiodic, because the monsters can change from any state to any state in both an even and an odd number of state changes. Without the secret passage, the Markov chain would be periodic, because then a transition from an even to an even state or from an odd to an odd state would only be possible with an even number of changes of state.

Because of the irreducibility and aperiodicity there is exactly one stable equilibrium distribution which the Markov chain assumes after an infinitely long time. The probabilities of staying in the individual states (almost) no longer change after a long time. The stationary distribution can be naively determined by entering the equation

${\displaystyle \pi _{n}=\pi _{0}\cdot P^{n}}$

a large one is substituted for any starting distribution because the matrix powers converge as in the example above. To compute an analytical solution is the linear system of equations ${\displaystyle \pi _{0}}$ ${\displaystyle n}$

${\displaystyle \pi =\pi \cdot P}$

to be resolved, under the secondary condition of a line total of . Substituting the naive solution into this equation serves as a control. The above equation is equivalent to ${\displaystyle \pi }$ ${\displaystyle 1}$

${\displaystyle (P^{T}-I)\cdot \pi ^{T}=0}$.

The transition matrix is ​​therefore transposed and the identity matrix subtracted. The desired vector of the state probabilities is now a column vector. The solution of the linear system of equations gives

${\displaystyle \pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)}$%.

The ghosts are most often in the center, less often on the edge and least often in the corner. The marginal states and , which are visited just as often on average as the central playing field are an exception . ${\displaystyle 2}$ ${\displaystyle 8}$

Countably infinite state space

Let us consider a Markov chain on the state space with transition probabilities ${\displaystyle Z=\mathbb {N} _{0}}$

${\displaystyle p_{ij}={\begin{cases}{\frac {1}{i+1}},&{\text{ falls }}j=i+1,\\1-{\frac {1}{i+1}},&{\text{ falls }}j=0,\\0&{\text{sonst}}.\end{cases}}}$

So there is a certain probability that you will rise to a number one higher, if this does not happen you will start again at zero. The following applies:

1. all states communicate with each other, since every state can reach 0 and 0 reaches every state. Accordingly, the Markov chain is irreducible.
2. the return times are 0 and therefore the 0 has the period 1, so it is aperiodic. Because of the irreducibility, the entire Markov chain is then also aperiodic. ${\displaystyle \{2,3,4,\dotsc \}}$
3. The expected return time to 0 is given by

${\displaystyle \operatorname {E} (\tau _{00})=\sum _{k=2}^{\infty }{\frac {k}{(k-1)!}}\cdot (1-{\frac {1}{k}})=e}$

Thus the 0 is positively recurrent and, due to the irreducibility of the Markov chain, the entire chain is also positively recurrent.

The chain thus converges to an invariant distribution that is independent of the start distribution. Since we already know that , we can use the definition as a recursion equation and conclude that . The exception is that it is possible to calculate the stationary distribution directly. ${\displaystyle P_{\pi }(\{0\})={\frac {1}{e}}}$ ${\displaystyle P_{\pi }(\{i\})={\frac {1}{i!e}}}$

use

Stationary distributions have numerous practical uses. If one imagines the Markov chain as a point moving randomly through a graph, then the i-th component of the stationary distribution is exactly the relative probability of encountering it in state i. An example of this is the Ehrenfest model . It models the diffusion of molecules through a membrane. The steady state is exactly the concentration when a diffusion equilibrium has been established. Another example is the calculation of the PageRank using the random surfer model. Here the Markov chain models the behavior of an Internet user: there is a certain probability that he will select one of the links on the homepage on which he is located, otherwise he will select another homepage via browser. The stationary distribution is then the relative probability that the random surfer hits a certain page. This is then a measure of the importance of this page and also the standardized PageRank of this page.

In addition, stationary distributions play an important role in the Markov Chain Monte Carlo process. They are exactly the distributions that you want to sample.

literature

• Ulrich Krengel : Introduction to probability theory and statistics . 8th edition, Vieweg, 2005. ISBN 978-3-8348-0063-3
• Hans-Otto Georgii: Stochastics: Introduction to Probability Theory and Statistics , 4th edition, de Gruyter, 2009. ISBN 978-3-11-021526-7
• Christian Hesse: Applied probability theory : a well-founded introduction with over 500 realistic examples and tasks, Vieweg, Braunschweig / Wiesbaden 2003, ISBN 978-3-528-03183-1 .
• Achim Klenke: Probability Theory. 2nd Edition. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76317-8