Systematic risk

Systematic risk in the portfolio

In portfolio theory or in the capital asset pricing model, systematic risk is a residual residual risk that cannot be eliminated through risk diversification , even if the individual values in the portfolio are optimally mixed .

General

The systematic risk is - in theory - the basis on which an investor expresses his risk-adjusted return expectation , since he and all other market participants in the market can eliminate the unsystematic risk by clever mixing so that it does not have to be remunerated. The unsystematic risk , on the other hand, is understood to mean that portion that can be eliminated through risk diversification. The beta factor is a measure of the systematic risk .

Systematic risk, there is a risk premium because the investor or investor can not escape through risk diversification that risk.

Derivation

According to Bernoulli's (1738) expected value dispersion rule, investors aim for the portfolio with the lowest standard deviation and maximum return. To solve this problem, Harry Markowitz first considers the covariance of securities. The following applies to the covariance:

${\displaystyle Cov(i,j)=\rho _{ij}\cdot \sigma _{i}\cdot \sigma _{j}\longrightarrow \rho _{ij}={\frac {Cov(i,j)}{\sigma _{i}\cdot \sigma _{j}}}}$

It turns out that the correlation coefficient plays a decisive role here. The covariance therefore indicates a measure with which two securities i and j move together or diverge within a period of time. This is where Markowitz comes in and recognizes that the overall risk of the portfolio is essentially related to the weighting of the individual items ( ) and the relationship between the individual items. In more formal terms, the following relationship applies to the overall risk: ${\displaystyle \rho _{ij}}$ ${\displaystyle \sigma _{ij}}$ ${\displaystyle X_{i}}$

${\displaystyle Var(r)=\sigma ^{2}=\sum _{i=1}^{N}\sum _{j=1}^{N}{X_{i}X_{j}\sigma _{ij}}}$

Since the covariance of a security with itself results in its variance, the meaningfulness of this formula can be illustrated by the following table, which shows the influence of variance and covariance in the portfolio with n securities:

${\displaystyle {\begin{array}{|c|c|c|c|c|}&1&2&...&N\\\hline 1&X_{1}^{2}Var(r_{1})&X_{1}X_{2}Cov(r_{1},r_{2})&...&X_{1}X_{N}Cov(r_{1},r_{N})\\2&X_{1}X_{2}Cov(r_{1},r_{2})&X_{2}^{2}Var(r_{2})&...&X_{2}X_{N}Cov(r_{2},r_{N})\\...&...&...&...&...\\N&X_{1}X_{N}Cov(r_{1},r_{N})&X_{2}X_{N}Cov(r_{2},r_{N})&...&X_{N}^{2}Var(r_{N})\\\end{array}}}$

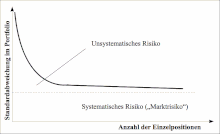
It can be seen that the number of terms of variance is. In contrast, the number of covariance terms is . It follows that the relationship between the individual values ​​of a portfolio becomes more relevant the greater the number of individual values ​​( ). Conversely, the relevance of the individual spread decreases with an increasing number of individual values ​​in the portfolio. The following applies: ${\displaystyle N}$ ${\displaystyle N^{2}-N}$ ${\displaystyle N}$

${\displaystyle \lim _{N\to \infty }Var(r)=\underbrace {\varnothing Cov(r_{i},r_{j})} _{SystematischesRisiko}}$

This theoretical finding agrees with empirical observations. It can be shown that with just a few securities, the portfolio risk can be significantly reduced, but not completely eliminated. So there seems to be some remaining risk. This risk is called systematic risk. It results from the mutual dependence of the selected individual items on the financial framework.

Individual evidence

1. ↑ Bernoulli, Daniel (transl. By Louise Sommer): Exposition of a New Theory on the Measurement of Risk, Econometrica, Vol. 22, No. 1, 1738
2. ↑ Statman, Meir: How many stocks make a diversified portfolio ?, in: Journal of Financial and Quantitative Analysis, Vol. 22, No. 3, 1987