Red–black tree

A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer who called them "symmetric binary B-trees", but acquired its modern name in a paper in 1978 by Leo J. Guibas and Robert Sedgewick. It is complex, but has good worst-case running time for its operations and is efficient in practice: it can search, insert, and delete in O(log n) time, where n is the number of elements in the tree.

Terminology

A red-black tree is a special type of binary tree, which is a structure used in computer science to organize pieces of comparable data, such as numbers. In binary trees, each piece of data is stored in a node. One of the nodes always functions as the starting place, and is not the child of any node; this is called the root node or root. It has up to two "children", other nodes to which it connects. Each of these children can have up to two children of its own, and so on. The root node thus has a path connecting it to any other node in the tree.

If a node has no children, it is called a leaf node, since intuitively it is at the periphery of the tree. A subtree is the portion of the tree that can be reached from a certain node, considered as a tree itself. In red-black trees, the leaves are assumed to be null; that is, they do not contain any data.

Binary search trees, including red-black trees, satisfy the constraint that every node contains a value less than or equal to all nodes in its right subtree, and greater than or equal to all nodes in its left subtree. This makes it possible to search the tree for a given value, and allows efficient in-order traversal of elements. As long as the tree is sufficiently balanced, it also makes a search quick.

Uses and advantages

Red-black trees offer worst-case guarantees for insertion time, deletion time, and search time. Not only does this make them valuable in time-sensitive applications such as real-time applications, but it makes them valuable building blocks in other data structures which provide worst-case guarantees; for example, many data structures used in computational geometry can be based on red-black trees.

AVL trees are more rigidly balanced than Red-Black trees and therefore in worst case scenarios require more rotations on insertion or deletion.

Red-black trees are also particularly valuable in functional programming, where they are one of the most common persistent data structures, used to construct associative arrays and sets which can retain previous versions after mutations. The persistent version of red-black trees requires O(log n) space for each insertion or deletion, in addition to time.

Red-black trees are an isometry of 2-3-4 trees. In other words, for every 2-3-4 tree, there exists at least one red-black tree with data elements in the same order. The insertion and deletion operations on 2-3-4 trees are also equivalent to color-flipping and rotations in red-black trees. This makes 2-3-4 trees an important tool for understanding the logic behind red-black trees, and this is why many introductory algorithm texts introduce 2-3-4 trees just before red-black trees, even though 2-3-4 trees are not often used in practice.

Properties

An example of a red-black tree

A red-black tree is a binary search tree where each node has a color attribute, the value of which is either red or black. In addition to the ordinary requirements imposed on binary search trees, the following additional requirements of any valid red-black tree apply:

1. A node is either red or black.
2. The root is black.
3. All leaves are black. (The leaves are the null children.)
4. Both children of every red node are black. Therefore, a black node is the only possible parent for a red node.
5. Every simple path from a node to a descendant leaf contains the same number of black nodes. (Not counting the leaf node.)

These constraints enforce a critical property of red-black trees: that the longest path from the root to a leaf is no more than twice as long as the shortest path from the root to a leaf in that tree. The result is that the tree is roughly balanced. Since operations such as inserting, deleting, and finding values requires worst-case time proportional to the height of the tree, this theoretical upper bound on the height allows red-black trees to be efficient in the worst-case, unlike ordinary binary search trees.

To see why these properties guarantee this, it suffices to note that no path can have two red nodes in a row, due to property 4. The shortest possible path has all black nodes, and the longest possible path alternates between red and black nodes. Since all maximal paths have the same number of black nodes, by property 5, this shows that no path is more than twice as long as any other path.

In many presentations of tree data structures, it is possible for a node to have only one child, and leaf nodes contain data. It is possible to present red-black trees in this paradigm, but it changes several of the properties and complicates the algorithms. For this reason, this article uses "null leaves", which contain no data and merely serve to indicate where the tree ends, as shown above. These nodes are often omitted in drawings, resulting in a tree which seems to contradict the above principles, but which in fact does not. A consequence of this is that all internal (non-leaf) nodes have two children, although one or more of those children may be a null leaf.

Some explain a red-black tree as a binary search tree whose edges, instead of nodes, are colored in red or black, but this does not make any difference. The color of a node in this article's terminology corresponds to the color of the edge connecting the node to its parent, except that the root node is always black (property 2) whereas the corresponding edge does not exist.

Operations

Read-only operations on a red-black tree require no modification from those used for binary search trees, because every red-black tree is a specialization of a simple binary search tree. However, the immediate result of an insertion or removal may violate the properties of a red-black tree. Restoring the red-black properties requires a small number (O(log n) or amortized O(1)) of color changes (which are very quick in practice) and no more than three tree rotations (two for insertion). Although insert and delete operations are complicated, their times remain O(log n).

Insertion

We begin by adding the node as we would in a simple binary search tree and coloring it red. What happens next depends on the color of other nearby nodes. We will use the term uncle node to refer to the sibling of a node's parent, as in human family trees. Note that:

• Property 3 (All leaves, including nulls, are black) always holds.
• Property 4 (Both children of every red node are black) is threatened only by adding a red node, repainting a black node red, or a rotation.
• Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is threatened only by adding a black node, repainting a red node black, or a rotation.

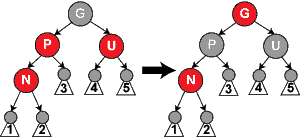
Note: We will use the label N for the node being inserted, P for N's parent node, G for N's grandparent, and U for N's uncle. Note, that in between some cases, we exchange the roles and labels of the nodes, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by these assumptions.

We will demonstrate each case with example C code. The uncle and grandparent nodes can be found by these functions:

node grandparent(node n) {
    return n->parent->parent;
}

node uncle(node n) {
    if (n->parent == grandparent(n)->left)
        return grandparent(n)->right;
    else
        return grandparent(n)->left;
}

Case 1: The new node N is at the root of the tree. In this case, we repaint it black to satisfy Property 2 (The root is black). Since this adds one black node to every path at once, Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is not violated.

void insert_case1(node n) {
    if (n->parent == NULL)
        n->color = BLACK;
    else
        insert_case2(n);
}

Case 2: The new node's parent P is black, so Property 4 (Both children of every red node are black) is not invalidated. In this case, the tree is still valid. Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is not threatened, because the new node N has two black leaf children, but because N is red, the paths through each of its children have the same number of black nodes as the path through the leaf it replaced, which was black, and so this property remains satisfied.

void insert_case2(node n) {
    if (n->parent->color == BLACK)
        return; /* Tree is still valid */
    else
        insert_case3(n);
}

Note: In the following cases we can assume that N has a grandparent node G, because its parent P is red, and if it were the root, it would be black. Thus, N also has an uncle node U, although it may be a leaf in cases 4 and 5.

Diagram of case 3 Case 3: If both the parent P and the uncle U are red, then we can repaint them both black and repaint the grandparent G red (to maintain Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes)). Now our new red node N has a black parent. Since any path through the parent or uncle must pass through the grandparent, the number of black nodes on these paths has not changed. However, the grandparent G may now violate properties 2 (The root is black) or 4 (Both children of every red node are black) (property 4 possibly being violated since G may have a red parent). To fix this, we perform this entire procedure recursively on G from case 1. Note that this is the only recursive call, and it occurs prior to any rotations, which proves that a constant number of rotations occur.

void insert_case3(node n) {
    if (uncle(n) != NULL && uncle(n)->color == RED) {
        n->parent->color = BLACK;
        uncle(n)->color = BLACK;
        grandparent(n)->color = RED;
        insert_case1(grandparent(n));
    }
    else
        insert_case4(n);
}

Note: In the remaining cases, we assume the parent node P is the left child of its parent. If it is the right child, left and right should be reversed throughout cases 4 and 5. The code samples take care of this.

Diagram of case 4 Case 4: The parent P is red but the uncle U is black; also, the new node N is the right child of P, and P in turn is the left child of its parent G. In this case, we can perform a left rotation that switches the roles of the new node N and its parent P; then, we deal with the former parent node P using Case 5 (relabeling N and P) because property 4 (Both children of every red node are black) is still violated. The rotation causes some paths (those in the sub-tree labelled "1") to pass through the new node where they did not before, but both these nodes are red, so Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is not violated by the rotation.

void insert_case4(node n) {
    if (n == n->parent->right && n->parent == grandparent(n)->left) {
        rotate_left(n->parent);
        n = n->left;
    } else if (n == n->parent->left && n->parent == grandparent(n)->right) {
        rotate_right(n->parent);
        n = n->right;
    }
    insert_case5(n);
}

Diagram of case 5 Case 5: The parent P is red but the uncle U is black, the new node N is the left child of P, and P is the left child of its parent G. In this case, we perform a right rotation on the grandparent G; the result is a tree where the former parent P is now the parent of both the new node N and the former grandparent G. We know that G is black, since its former child P could not have been red otherwise. We then switch the colors of P and G, and the resulting tree satisfies Property 4 (Both children of every red node are black). Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) also remains satisfied, since all paths that went through any of these three nodes went through G before, and now they all go through P. In each case, this is the only black node of the three.

void insert_case5(node n) {
    n->parent->color = BLACK;
    grandparent(n)->color = RED;
    if (n == n->parent->left && n->parent == grandparent(n)->left) {
        rotate_right(grandparent(n));
    } else {
        /* Here, n == n->parent->right && n->parent == grandparent(n)->right */
        rotate_left(grandparent(n));
    }
}

Note that inserting is actually in-place, since all the calls above use tail recursion.

Removal

In a normal binary search tree, when deleting a node with two non-leaf children, we find either the maximum element in its left subtree or the minimum element in its right subtree, and move its value into the node being deleted (as shown here). We then delete the node we copied the value from, which must have less than two non-leaf children. Because merely copying a value does not violate any red-black properties, this reduces the problem of deleting to the problem of deleting a node with at most one non-leaf child. It does not matter whether this node is the node we originally wanted to delete or the node we copied the value from.

For the remainder of this discussion we can assume we are deleting a node with at most one non-leaf child, which we will call its child (if it has only leaf children, let one of them be its child). If we are deleting a red node, we can simply replace it with its child, which must be black. All paths through the deleted node will simply pass through one less red node, and both the deleted node's parent and child must be black, so properties 3 (All leaves, including nulls, are black) and 4 (Both children of every red node are black) still hold. Another simple case is when the deleted node is black and its child is red. Simply removing a black node could break Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes), but if we repaint its child black, both of these properties are preserved.

The complex case is when both the node to be deleted and its child is black. We begin by replacing the node to be deleted with its child. We will call (or label) this child (in its new position) N, and its sibling (its new parent's other child) S. In the diagrams below, we will also use P for N's new parent, S_L for S's left child, and S_R for S's right child (it can be shown that S cannot be a leaf).

Note: In between some cases, we exchange the roles and labels of the nodes, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by these assumptions. White represents an unknown color (either red or black).

We will find the sibling using this function:

node sibling(node n) {
     if (n == n->parent->left)
         return n->parent->right;
     else
         return n->parent->left;
}

Note: In order that the tree remains well-defined, we need that every null leaf remains a leaf after all transformations (that it will not have any children). If the node we are deleting has a non-leaf (non-null) child N, it is easy to see that the property is satisfied. If, on the other hand, N would be a null leaf, it can be verified from the diagrams (or code) for all the cases that the property is satisfied as well.

We can perform the steps outlined above with the following code, where the function replace_node substitutes child into n's place in the tree. For convenience, code in this section will assume that null leaves are represented by actual node objects rather than NULL (the code in the Insertion section works with either representation).

void delete_one_child(node n) {
    /* Precondition: n has at most one non-null child */
    node child = is_leaf(n->right) ? n->left : n->right;
    replace_node(n, child);
    if (n->color == BLACK) {
        if (child->color == RED)
            child->color = BLACK;
        else
            delete_case1(child);
    }
    free(n);
}

Note: If N is a null leaf and we do not want to represent null leaves as actual node objects, we can modify the algorithm by first calling delete_case1() on its parent (the node that we delete, n in the code above) and deleting it afterwards. We can do this because the parent is black, so it behaves in the same way as a null leaf (and is sometimes called a 'phantom' leaf). And we can safely delete it at the end as n will remain a leaf after all operations, as shown above.

If both N and its original parent are black, then deleting this original parent causes paths which proceed through N to have one fewer black node than paths that do not. As this violates Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes), the tree must be rebalanced. There are several cases to consider:

Case 1: N is the new root. In this case, we are done. We removed one black node from every path, and the new root is black, so the properties are preserved.

void delete_case1(node n) {
    if (n->parent == NULL)
        return;
    else
        delete_case2(n);
}

Note: In cases 2, 5, and 6, we assume N is the left child of its parent P. If it is the right child, left and right should be reversed throughout these three cases. Again, the code examples take both cases into account.

Diagram of case 2 Case 2: S is red. In this case we reverse the colors of P and S, and then rotate left at P, turning S into N's grandparent. Note that P has to be black as it had a red child. Although all paths still have the same number of black nodes, now N has a black sibling and a red parent, so we can proceed to step 4, 5, or 6. (Its new sibling is black because it was once the child of the red S.) In later cases, we will relabel N's new sibling as S.

void delete_case2(node n) {
    if (sibling(n)->color == RED) {
        n->parent->color = RED;
        sibling(n)->color = BLACK;
        if (n == n->parent->left)
            rotate_left(n->parent);
        else
            rotate_right(n->parent);
    }
    delete_case3(n);
}

Diagram of case 3 Case 3: P, S, and S's children are black. In this case, we simply repaint S red. The result is that all paths passing through S, which are precisely those paths not passing through N, have one less black node. Because deleting N's original parent made all paths passing through N have one less black node, this evens things up. However, all paths through P now have one fewer black node than paths that do not pass through P, so Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is still violated. To correct this, we perform the rebalancing procedure on P, starting at case 1.

void delete_case3(node n) {
    if (n->parent->color == BLACK &&
        sibling(n)->color == BLACK &&
        sibling(n)->left->color == BLACK &&
        sibling(n)->right->color == BLACK)
    {
        sibling(n)->color = RED;
        delete_case1(n->parent);
    }
    else
        delete_case4(n);
}

Diagram of case 4 Case 4: S and S's children are black, but P is red. In this case, we simply exchange the colors of S and P. This does not affect the number of black nodes on paths not going through N, but it does add one to the number of black nodes on paths going through N, making up for the deleted black node on those paths.

void delete_case4(node n) {
    if (n->parent->color == RED &&
        sibling(n)->color == BLACK &&
        sibling(n)->left->color == BLACK &&
        sibling(n)->right->color == BLACK)
    {
        sibling(n)->color = RED;
        n->parent->color = BLACK;
    }
    else
        delete_case5(n);
}

Diagram of case 5 Case 5: S is black, S's left child is red, S's right child is black, and N is the left child of its parent. In this case we rotate right at S, so that S's left child becomes S's parent and N's new sibling. We then exchange the colors of S and its new parent. All paths still have the same number of black nodes, but now N has a black sibling whose right child is red, so we fall into case 6. Neither N nor its parent are affected by this transformation. (Again, for case 6, we relabel N's new sibling as S.)

void delete_case5(node n) {
    if (n == n->parent->left &&
        sibling(n)->color == BLACK &&
        sibling(n)->left->color == RED &&
        sibling(n)->right->color == BLACK)
    {
        sibling(n)->color = RED;
        sibling(n)->left->color = BLACK;
        rotate_right(sibling(n));
    }
    else if (n == n->parent->right &&
             sibling(n)->color == BLACK &&
             sibling(n)->right->color == RED &&
             sibling(n)->left->color == BLACK)
    {
        sibling(n)->color = RED;
        sibling(n)->right->color = BLACK;
        rotate_left(sibling(n));
    }
    delete_case6(n);
}

Diagram of case 6 Case 6: S is black, S's right child is red, and N is the left child of its parent P. In this case we rotate left at P, so that S becomes the parent of P and S's right child. We then exchange the colors of P and S, and make S's right child black. The subtree still has the same color at its root, so Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) are not violated. However, N now has one additional black ancestor: either P has become black, or it was black and S was added as a black grandparent. Thus, the paths passing through N pass through one additional black node. Meanwhile, if a path does not go through N, then there are two possibilities: It goes through N's new sibling. Then, it must go through S and P, both formerly and currently, and they have only exchanged colors. Thus the path contains the same number of black nodes. It goes through N's new uncle, S's right child. Then, it formerly went through S, S's parent, and S's right child, but now only goes through S, which has assumed the color of its former parent, and S's right child, which has changed from red to black. The net effect is that this path goes through the same number of black nodes. Either way, the number of black nodes on these paths does not change. Thus, we have restored Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes). The white node in the diagram can be either red or black, but must refer to the same color both before and after the transformation.

void delete_case6(node n) {
    sibling(n)->color = n->parent->color;
    n->parent->color = BLACK;
    if (n == n->parent->left) {
        /* Here, sibling(n)->right->color == RED */
        sibling(n)->right->color = BLACK;
        rotate_left(n->parent);
    }
    else
    {
        /* Here, sibling(n)->left->color == RED */
        sibling(n)->left->color = BLACK;
        rotate_right(n->parent);
    }
}

Again, the function calls all use tail recursion, so the algorithm is in-place. Additionally, no recursive calls will be made after a rotation, so a constant number of rotations (up to 3) are made.

Proof of asymptotic bounds

A red black tree which contains n internal nodes has a height of O(log(n)).

Definitions:

• h(v) = height of subtree rooted at node v
• bh(v) = the number of black nodes (not counting v if it is black) from v to any leaf in the subtree (called the black-height).

Lemma: A subtree rooted at node v has at least $2^{bh(v)}-1$ internal nodes.

Proof of Lemma (by induction height):

Basis: h(v) = 0

If v has a height of zero then it must be null, therefore bh(v) = 0. So:

$2^{bh(v)}-1=2^{0}-1=1-1=0$

Inductive Hypothesis: v such that h(v) = k, has $2^{bh(v)}-1$ internal nodes implies that $v'$ such that h($v'$) = k+1 has $2^{bh(v')}-1$ internal nodes.

Since $v'$ has h($v'$) > 0 it is an internal node. As such it has two children which have a black-height of either bh($v'$) or bh($v'$)-1 (depending on whether $v'$ is red or black). By the inductive hypothesis each child has at least $2^{bh(v')-1}-1$ internal nodes, so $v'$ has:

$2^{bh(v')-1}-1+2^{bh(v')-1}-1+1=2^{bh(v')}-1$

internal nodes.

Using this lemma we can now show that the height of the tree is logarithmic. Since at least half of the nodes on any path from the root to a leaf are black (property 4 of a red black tree), the black-height of the root is at least h(root)/2. By the lemma we get:

$n\geq 2^{h({\text{root}}) \over 2}-1\leftrightarrow \;\log _{2}{(n+1)}\geq {h({\text{root}}) \over 2}\leftrightarrow \;h({\text{root}})\leq 2\log _{2}{(n+1)}$

Therefore the height of the root is O(log(n)).

Complexity

In the tree code there is only one loop where the node of the root of the red-black property that we wish to restore, x, can be moved up the tree by one level at each iteration.

Since the original height of the tree is O(log n), there are O(log n) iterations. So overall the insert routine has O(log n) complexity.

References

• Mathworld: Red-Black Tree
• San Diego State University: CS 660: Red-Black tree notes, by Roger Whitney
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Chapter 13: Red-Black Trees, pp.273–301.
• Pfaff, Ben (2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University. {{cite web}}: Unknown parameter |month= ignored (help)
• Okasaki, Chris. "Red-Black Trees in a Functional Setting" (PS).

External links

Demos

• Red/Black Tree Demonstration, an interactive demo of insertion and removal with Java source code
• Red-Black Tree Animation, a demo of worst-case insertion
• aiSee: Visualization of a Sorting Algorithm, an animated GIF showing insertion (200KB)
• Red-Black Tree Demonstration, a demo of insertion with Java source code by David M. Howard
• AVL Tree Applet, an interactive demo of insertion to and removal from AVL, splay and red-black trees

Implementations

• In the C++ Standard Template Library, the containers std::set<Value> and std::map<Key,Value> are often based on red-black trees
• Efficient implementation of Red-Black Trees
• RBT: A SmallEiffel Red-Black Tree Library
• libredblack: A C Red-Black Tree Library
• Red-Black Tree C Code
• Red-Black Tree Java implementation in java.util.TreeMap
• DragonFlyBSD VM subsystems utilize Red-Black trees
• NATURAL/ADABAS implementation by Paul Macgowan
• NGenerics : implementation in C#