5-polytope
 5-simplex (Hexateron) |
 5-orthoplex (Pentacross) |
 5-cube (Penteract) |
 5-demicube (Demipenteract) |
| Graphs of three regular 5-polytopes and one semiregular form. | |||
|---|---|---|---|
In geometry, a five-dimensional polytope, or 5-polytope, is a polytope in 5-dimensional space. Each polyhedral cell being shared by exactly two polychoron facets.
A proposed name polyteron (plural: polytera) has been advocated, from the Greek root poly- meaning "many", a shortened tetra- meaning "four", and suffix -on. "Four" refers to the dimension of the 5-polytope facets.
Definition
A 5-polytope, or polyteron, is a closed five-dimensional figure with vertices, edges, faces, and cells, and hypercells. A vertex is a point where five or more edges meet. An edge is a line segment where four or more faces meet, and a face is a polygon where three or more cells meet. A cell is a polyhedron, and a hypercell is a polychoron. Furthermore, the following requirements must be met:
- Each cell must join exactly two hypercells.
- Adjacent hypercells are not in the same four-dimensional hyperplane.
- The figure is not a compound of other figures which meet the requirements.
Regular and uniform 5-polytopes by fundamental Coxeter groups
Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} polychoral facets around each face.
Uniform 5-polytopes can be generated by fundamental finite Coxeter groups and represented by permutations of rings of the Coxeter-Dynkin diagrams.
There are three regular and many other uniform 6-polytopes, enumerated by Coxeter groups, two having linear graphs and one having a bifurcated graph.
- Simplex family: A5 [3,3,3,3] -









- 19 uniform 5-polytopes as permutations of rings in the group diagram, including one regular:
- {3,3,3,3} - 5-simplex, hexateron, or hexa-5-tope .
- 19 uniform 5-polytopes as permutations of rings in the group diagram, including one regular:
- Hypercube/orthoplex family: B5 [4,3,3,3] -









- 31 uniform 5-polytopes as permutations of rings in the group diagram, including two regular forms:
- {4,3,3,3} — 5-cube, penteract, or deca-5-tope.









- {3,3,3,4} — 5-orthoplex, pentacross, or triacontadi-5-tope.









- {4,3,3,3} — 5-cube, penteract, or deca-5-tope.
- 31 uniform 5-polytopes as permutations of rings in the group diagram, including two regular forms:
- Demihypercube D5/E5 family: [32,1,1] -







- 23 uniform 5-polytopes as permutations of rings in the group diagram, including:
- {31,2,1}, 12,1 demipenteract -
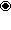





 ; also as h{4,3,3,3},
; also as h{4,3,3,3}, 








- {32,1,1}, 21,1 pentacross -






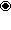
- {31,2,1}, 12,1 demipenteract -
- 23 uniform 5-polytopes as permutations of rings in the group diagram, including:
Uniform prismatic forms
There are 6 categorical uniform prismatic families of polytopes based on the uniform 4-polytopes:
| # | Coxeter groups | Coxeter graph | Uniform polytopes | |
|---|---|---|---|---|
| 1 | A4 × A1 | [3,3,3] × [ ] | 9 uniform polytopes based on the regular 5-cell | |
| 2 | B4 × A1 | [4,3,3] × [ ] | 15 based on the regular tesseract or 16-cell | |
| 3 | F4 × A1 | [3,4,3] × [ ] | 9 based on the regular 24-cell | |
| 4 | H4 × A1 | [5,3,3] × [ ] | 15 based on the regular 120-cell or 600-cell | |
| 5 | D4 × A1 | [31,1,1] × [ ] | 8 based on the demitesseract (16-cell). | |
| 6 | I2(p) × I2(q) × A1 | [p] × [q] × [ ] | Infinitely many based on the uniform duoprisms. | |
Uniform duoprismatic forms
There are 3 categorical uniform duoprismatic families of polytopes based on Cartesian products of the uniform polyhedra and regular polygons: {q,r}×{p}:
| # | Coxeter groups | Coxeter graph | |
|---|---|---|---|
| 1 | A3 × I2(p) | [3,3] × [p] | |
| 2 | B3 × I2(p) | [4,3] × [p] | |
| 3. | H3 × I2(p) | [5,3] × [p] | |
Wythoff construction for the uniform 5-polytopes
Construction of the reflective 5-dimensional uniform polytopes are done through a Wythoff construction process, and represented through a Coxeter-Dynkin diagram, where each node represents a mirror. Nodes are ringed to imply which mirrors are active. The full set of uniform polytopes generated are based on the unique permutations of ringed nodes. Uniform 5-polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may have two ways of naming them.
Here's the primary operators available for constructing and naming the uniform 5-polytopes.
The last operation, the snub, and more generally the alternation, are the operation that can create nonreflective forms. These are drawn with "hollow rings" at the nodes.
The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.
| Operation | Extended Schläfli symbol |
Coxeter- Dynkin diagram |
Description |
|---|---|---|---|
| Parent | t0{p,q,r,s} | Any regular 4-polytope | |
| Rectified | t1{p,q,r,s} | The edges are fully truncated into single points. The 4-polytope now has the combined faces of the parent and dual. | |
| Birectified | t2{p,q,r,s} | Birectification reduces cells their duals. | |
| Truncated | t0,1{p,q,r,s} | Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 4-polytope. The 4-polytope has its original faces doubled in sides, and contains the faces of the dual.
| |
| Cantellated | t0,2{p,q,r,s} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place. A uniform cantellation is half way between both the parent and dual forms.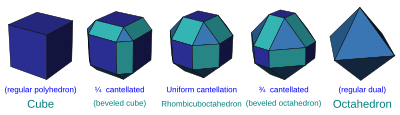
| |
| Runcinated | t0,3{p,q,r,s} | Runcination reduces facet cells and creates new cells at the vertices and edges. | |
| Stericated | t0,4{p,q,r,s} | Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. | |
| Omnitruncated | t0,1,2,3,4{p,q,r,s} | All four operators, truncation, cantellation, runcination, and sterication are applied. | |
| Snub | s{p,q,q,s} | The snub takes the omnitruncated form and rectifies alternate vertices. |
Regular and uniform honeycombs
There's one regular honeycomb of Euclidean 4-space, the penteractic honeycomb, with symbols {4,32,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
There's also the demihexeractic honeycomb, a uniform tessellation, with symbols h{4,32,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Pyramids
Pyramidal polyterons, or 5-pyramids, can be generated by a polychoron base in a 4-space hyperplane connected to a point off the hyperplane. The 5-simplex is the simplest example with a 4-simplex base.
A note on generality of terms for n-polytopes and elements
A 5-polytope, or polyteron, follows from the lower dimensional polytopes: 2: polygon, 3: polyhedron, and 4: polychoron.
Although there is no agreed upon standard terminology for higher polytopes, for dimensional clarity George Olshevsky advocates borrowing from the SI prefix sequencing, which can covers up to 10-polytopes with 9-dimensional facets:
- Polyteron for a 5-polytope (tera, a shortened on tetra-, for 4D faceted polytope), and terons for 4-face element.
- Polypeton for a 6-polytope (peta, a shortened on penta-, for 5D faceted polytope), and petons for 5-face elements.
- Polyexon for a 7-polytope (exa or ecta, a shortened on hexa-, for 6D faceted polytope), and exons for 6-face elements.
- Polyzetton for a 8-polytope (zetta, a variation on hepta-, for 7D faceted polytope), and zettons for 7-face elements.
- Polyyotton for a 9-polytope (yotta, a variation on octa-, for 8D faceted polytope), and yottons for 8-face elements.
- Polyxennon for a 10-polytope (xenna, a variation on ennea-, for 9D faceted polytope), and xennons for 9-face elements.
For specific polytopes, like the lower dimensional polytopes, they can be named by their number of facets. For example a 5-simplex, with 6 facets can explicitly be called a hexa-5-tope, representing a 6-faceted 5-polytope, and thus is named a hexateron.
See also
- List of regular polytopes#Five Dimensions
- Polygon - 2-polytopes
- Polyhedron - 3-polytopes
- Polychoron - 4-polytopes
- 6-polytope
- 7-polytope
- 8-polytope
- 9-polytope
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
External links
- Polytope names, Guy Inchbald
- Polytopes of Various Dimensions, Jonathan Bowers
- Glossary for hyperspace: Polytope, George Olshevsky
- Multi-dimensional Glossary, Garrett Jones
- polytope names, Wendy Krieger
