Self-dual polyhedron

In geometry, a self-dual polyhedron is a polyhedron whose dual polyhedron is a congruent figure.

A self-dual polyhedron must have the same number of vertices as faces. We can distinguish between structural (topological) duality and geometrical duality. The topological structure of a self-dual polyhedron is also self-dual. Whether or not such a polyhedron is also geometrically self-dual will depend on the particular geometrical duality being considered.

More generally the property of self-duality includes self-dual polytopes and tessellations of any dimension.

Polygons

All regular polygons are self-dual, with equal number of vertices and edges.

In addition the regular star polygons and regular star figures (compounds), being composed of regular polygons, are also self-dual.

Self-dual polyhedra

The commonest geometric arrangement is where some convex polyhedron is in its canonical form, which is to say that the all its edges must be tangent to a certain sphere whose centre coincides with the centre of gravity (average position) of the tangent points. If the polar reciprocal of the canonical form in the sphere is congruent to the original, then the figure is self-dual.

There are infinitely many self-dual polyhedra. The simplest infinite family are the pyramids of n sides and of canonical form. Another infinite family consists of polyhedra that can be roughly described as a pyramid sitting on top of a prism (with the same number of sides). Add a frustum (pyramid with the top cut off) below the prism and you get another infinite family, and so on.

There are many other convex, self-dual polyhedra. For example, there are 6 different ones with 7 vertices, and 16 with 8 vertices. ^{[citation needed]}

Non-convex self-dual polyhedra can also be found, for example there is one among the facettings of the regular dodecahedron (and hence by duality also among the stellations of the icosahedron).

Family of pyramids
Tetrahedron	Square pyramid	Pentagonal pyramid	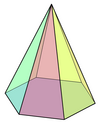Hexagonal pyramid

Family of elongated pyramids
Elongated triangular pyramid	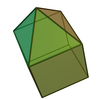Elongated square pyramid	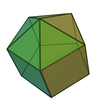Elongated pentagonal pyramid

Self dual compound polyhedra

The Stella octangula, being a compound of two tetrahedra is also self-dual, as well as four other regular-dual compounds.

Self-dual polytopes

Every regular n-simplex, with Schlafli symbol {3ⁿ}, is self-dual.

For polychora, the 24-cell polychoron, with Schlafli symbol {3,4,3}, is self-dual.

Self-dual Tessellations

Tilings and honeycombs can also be self-dual. All n-dimensional hypercubic honeycombs with Schlafli symbols {4,3ⁿ⁻²,4}, are self-dual.

A {4,4} square tiling with its dual drawn in red.

References

B. Grünbaum, Convex Polytopes, Springer, New York 2003, page 48.
Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0 (Page 28: A Polytope is self-dual if it is isomorphic to its dual.)

External links

This geometry-related article is a stub. You can help Wikipedia by expanding it.