Dispersion (water waves)

This article is about dispersion of waves on a water surface. For other forms of dispersion, see dispersion.

In fluid dynamics, dispersion of water waves generally refers to frequency dispersion. Frequency dispersion means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension. As a result, water with a free surface is generally considered to be a dispersive medium.

Besides frequency dispersion, water waves also exhibit amplitude dispersion. This is a nonlinear effect, by which waves of larger amplitude have a different phase speed from small-amplitude waves.

Overview

Phase velocity

Dispersion of gravity waves on a fluid surface. Phase and group velocity divided by shallow-water phase velocity √(gh) as a function of relative depth h / λ. A: phase velocity, B: group velocity, C: phase and group velocity √(gh) valid in shallow water. Drawn lines: based on dispersion relation valid in arbitrary depth. Dashed lines: deep water limits.

Dispersion of gravity waves on a fluid surface. Phase and group velocity divided by deep-water phase velocity √(½ gλ / π) as a function of relative depth h / λ. A: phase velocity, B: group velocity, C: phase and group velocity √(gh) valid in shallow water. Drawn lines: based on dispersion relation valid in arbitrary depth. Dashed lines: deep water limits.

A sinusoidal wave, of small surface-elevation amplitude and with a constant wavelength, propagates with the phase velocity, also called celerity or phase speed. According to linear theory for waves forced by gravity, the phase speed depends on the wavelength and the water depth. For a fixed water depth, long waves (with large wavelength) propagate faster than shorter waves.

Group velocity

Frequency dispersion in bichromatic groups of gravity waves on the surface of deep water. The red dot moves with the phase velocity, and the green dots propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The red dot overtakes two green dots, when moving from the left to the right of the figure.
New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.
For gravity surface-waves, the water particle velocities are much smaller than the phase velocity, in most cases.

Multi-component wave patterns

Frequency dispersion of surface gravity waves on deep water. The superposition (dark blue line) of three wave components (light blue lines), with respectively 22 (bottom), 25 (middle) and 29 (top) wavelengths fitting in a horizontal domain of 2,000 meter length, is shown. The component with the shortest wavelength (top) propagates slowest. The wave amplitudes of the components are respectively 1, 2 and 1 meter. The differences in wavelength and phase speed of the components results in a changing pattern of wave groups, due to amplification where the components are in phase, and reduction where they are in anti-phase.

The effect of frequency dispersion is that the velocity of the wave front travels as a function of wavelength, so that spatial and temporal phase properties of the propagating wave are constantly changing. For example, under the action of gravity, water waves with a longer wavelength travel faster than those with a shorter wavelength.

Linear dispersion relation for surface gravity waves

This phenomenon is expressed by the so-called linear dispersion relationship, which may be given as:

$\omega ^{2}=gk\,\tanh(kh).$

Here ω is the angular frequency, g is acceleration due to gravity, k is the wavenumber, and h is the depth. The hyperbolic tangent is meant to physically model the observation that dispersion asymptotically goes to zero as the relative water depth kh gets small.

Historically, this equation was derived by George Biddell Airy and published in about 1840. A similar equation was also derived by Philip Kelland at around the same time.

Celerity

The celerity (scalar valued velocity) or phase velocity of linear water waves may then be expressed as,

$C={\frac {\omega }{k}}={\sqrt {{\frac {g}{k}}\,\tanh(kh)}}.$

Approximations

The linear dispersion relation cannot be solved analytically when the variable to be solved for is the wavenumber k. Because this is frequently the case, approximations for deep and shallow water have been made.

Shallow water

The shallow water (with small kh) limit is defined as

$\omega ^{2}=ghk^{2}\,\$,

which was derived by Joseph Louis Lagrange. This results from the fact that the hyperbolic tangent function, when evaluated at small values, approaches the value being evaluated. That is,

$\lim _{kh\rightarrow 0}\tanh(kh)=kh\,\$.

Deep water

The deep water approximation (large kh) is

$\omega ^{2}=gk\,\$

and arises from the fact that the hyperbolic tangent function approaches a value of 1. That is,

$\lim _{kh\rightarrow \infty }\tanh(kh)=1\,\$.

Surface tension effects

Dispersion of gravity-capillary waves on a deep water. Phase and group velocity divided by $\scriptstyle {\sqrt[{4}]{g\sigma /\rho }}$ as a function of $\scriptstyle {\frac {1}{\lambda }}{\sqrt {\sigma /(\rho g)}}$.
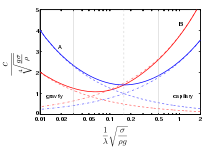
Blue lines (A): phase velocity, Red lines (B): group velocity.
Drawn lines: based on dispersion relation for gravity-capillary waves.
Dashed lines: based on dispersion relation for deep-water gravity waves.
Dash-dot lines: based on dispersion relation valid for capillary waves.

In case of gravity-capillary waves, where surface tension affects the waves, the dispersion relation becomes:

$\omega ^{2}=\left(gk+{\frac {\sigma }{\rho }}k^{3}\right)\tanh(kh),$

with σ the surface tension (in N/m).

Nonlinear effects

These equations are correct to the second-order perturbation theory expansion, in terms of the wave steepness k A, where A is wave amplitude. To the third order, and for deep water, the dispersion relation is,

$\omega ^{2}=gk\left[1+(kA)^{2}\right].$

This implies that large waves travel faster than small ones of the same frequency. This is only noticeable when the wave steepness k A is large.

Doppler shift

Water waves on a mean flow (so a wave in a moving medium) experience a Doppler shift. The dispersion relation for a non-moving medium is given as:

$\displaystyle \omega ^{2}=\Omega ^{2}(k),$

with k the wave wavenumber. Then for a medium with mean velocity vector V, the dispersion relationship with Doppler shift becomes:

$\left(\omega -{\mathbf {k}}\cdot {\mathbf {V}}\right)^{2}=\Omega ^{2}(k),$

where k is the wavenumber vector, related to k as: k = |k|.

See also

Other articles on dispersion

• Dispersive partial differential equation
• Dispersion relation
• Dispersion (optics)
• Phase velocity
• Group velocity

Dispersive water-wave models

• Benjamin-Bona-Mahony equation
• Boussinesq approximation (water waves)
• Davey–Stewartson equations
• Korteweg-de Vries equation or KdV equation
• Nonlinear Schrödinger equation
• Shallow water equations

References

• A.D.D. Craik (2004). "The origins of water wave theory". Annual Review of Fluid Mechanics. 36: 1–28. doi:10.1146/annurev.fluid.36.050802.122118.
• R. G. Dean and R. A. Dalrymple (1991). Water wave mechanics for engineers and scientists. Advanced Series on Ocean Engineering. Vol. 2. World Scientific, Singapore. ISBN 978-9810204204.
• M. W. Dingemans (1997). Water wave propagation over uneven bottoms. Advanced Series on Ocean Engineering. Vol. 13. World Scientific, Singapore. pp. 2 Parts, 967 pages. ISBN 981-02-0427-2.
• Phillips, O.M. (1977). The dynamics of the upper ocean (2^nd edition ed.). Cambridge University Press. ISBN 0-521-29801-6. {{cite book}}: |edition= has extra text (help)

External links

• Mathematical aspects of dispersive waves are discussed on the Dispersive Wiki.