Derivation (computer science)
In theoretical computer science, the process of generating a word according to the rules of a formal grammar is called derivation .
A word is understood to be any string of characters, i.e. a finite sequence of symbols . A formal grammar is a mathematical model that defines a set of such derivable words. This set is called a formal language . The one-time replacement of a section of a character string, according to one of the rules of formal grammar, represents a derivation step . The formal grammar also defines the symbols that a word may consist of, and those that are only used in the intermediate results of the derivation of a Word may occur. To derive a word, one begins with a special symbol, the start symbol, and then carries out derivation steps one after the other (if suitable rules are selected) until the word has finally been generated.
scope of application
The question of whether a word belongs to a language is called a word problem . Whether a word belongs to the language of a grammar is defined by whether a derivative of the word exists. A derivation of a word according to the rules of a grammar is therefore a mathematical proof that the word belongs to the language of the given grammar.
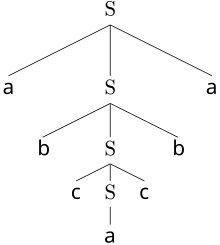
With suitable grammars (the context-free ones ), a derivation tree results from the derivation of a word . There is usually exactly one derivation tree for a derivation. But if there are several derivations for a word that also result in different derivation trees, the grammar is ambiguous .
The syntax analysis part (“ parser ”) of a compiler analyzes the source text of a program using the grammar rules of the programming language used. He also determines whether the program is a word of the programming language in question, i.e. whether it is syntactically correct. When analyzing the source code, the parser looks indirectly for a derivation. If it fails because the program contains a syntax error , it is proven that no derivation exists for the program.
In the genetic programming used to a random approach According derivation trees of a grammar to generate solutions.
Definitions
Be a Chomsky grammar . stands for the finite alphabet of the terminals , i.e. for characters (of the language to be generated) that are not further derived. represents the whole vocabulary of characters, in addition to the terminals, the nonterminals or nonterminal symbols from , so the characters must be converted yet to terminals (and occasionally therefore variables are called). The start symbol is a non-terminal. A character cannot be terminal and nonterminal at the same time. The production rules describe how the non-terminals are derived from the terminals.
Some authors alternatively call the quadruple as grammar with the requirement that the disjunction of Nonterminal- and terminal Quantity: ; In some cases, other names are also used for the individual components.
Sentence form
A kit form of a grammar is a sequence of symbols or : .
Derivation step
A derivation step is a part of a derivation that converts one to one with a production rule. and are consequences from terminals and non-terminals. A derivation rule is formally noted as . The permissible and subject to it, depending on the type of grammar, more or less severe restrictions.
If a word is present, the production rule can to apply, with the resulting word . Then you write (or also ). To indicate which production rule was used, one also writes . Formally the relation on the set of all words from terminals and non-terminals is given by
- .
Drainage piece
A derivative part is a finite sequence of sentence forms, in which each subsequent one always arises from the immediate predecessor through a derivative step. Written briefly
If several rules are applied at once, one writes (analogous to Kleen's envelope , see: Relations §Homogeneous Relations ). Formally, the relation can be represented as a union as follows:
Derivation
A derivative is a derivative piece that begins with the start symbol and whose last sentence form is a word. A derivation (in n steps) can therefore be noted as, whereby only contains terminal symbols. Disregarding the (finite) number of steps leads to , if from can be derived.
Generated language
The language generated by is the set of all words above the character alphabet that come at the end of a derivative; one also says that can be derived.
In general, several different productions can be applied to one sentence form, and one and the same production can also be applicable in different places.
Examples
Language of the palindromes
Palindromes can be generated using a context-free grammar. In the example we restrict ourselves to an alphabet made up of the three letters , and .
- with and
stands for the empty word .
With this grammar all palindromes from , and existing can be generated. One derivation of the word is .
Positive even integer language
A formal notation of the grammar has been dispensed with at this point. The numbers can have any number of leading zeros.
The terminals are the numbers from to ( ), serve as non-terminals and ( ), the latter also being the start symbol:
The production rules are:
,
( is an abbreviation for )
The derivation begins with a rule that contains the start symbol on the left . For example, the derivative begins with . The one at the end cannot be removed by rule applications, so the resulting number is definitely even. This must now be replaced according to one of the rules with on the left. A possible continuation of the derivation is . Other digits can also be generated; Since at the end of the derivation all non-terminals must have disappeared, the rule must apply at some point . is the empty word, colloquial you can say that nothing will replace it. The example derivation is therefore concluded with .
Any positive, even number can be generated with the production rules. They cannot produce other numbers.
Language of the line numbers
The language of the line numbers is generated by
- ,
where is denoted by the number line. The derivation that leads to the 5 line number is roughly:
In the case of this grammar, each sentence form does not contain the Z once or exactly once, which in this case is always at the end of the sentence form. So all derivatives are legal derivatives. With this grammar, every line number has exactly one possible derivation.
The same language is also generated from the grammar
- .
The following is a derivation for the 3-line number:
- .
Note that in the second step it remains unclear whether the right or left in is replaced by another ; both times arises initially . With the indication that it is a legal derivation, the substitution position becomes clear. The same clarity is achieved if you always the exact location of the replacement, the so-called Henkel (English handle indicates) with.
Parsing
The reverse process, in which a word is given and a derivation is sought, is also called parsing . Here, automata are used to check whether the given word can have originated from the derivation rules . The syntax check for programming languages is of particular importance. Since these are often context-free languages , a push -down machine is necessary.
Legal derivation
A derivation means rightmost derivation (English rightmost derivation ) when in each of its individual steps the rightmost always non-terminal symbol of the set form a production is replaced invention.
Note: One speaks of legal derivation only if a context-free grammar (Chomsky grammar of type 2) is available; Such grammars are also the most common type of language in computer science practice. In this case, every production has the simple form , so all left sides are individual non-terminal symbols, the right sides remain arbitrary. Therefore, the single derivation step replaces an occurrence of a non-terminal symbol in the output set by a form of the possible right sides with .
In the case of legal derivations, it is sufficient to simply state the sequence of productions used to clearly describe the overall replacement process (which replacements in which places ?) And its result, which is not the case for any derivations because a sentence form that occurs can contain multiple non-terminal symbols .
In the area of compiler construction , legal derivations are important because an efficient method of syntax analysis is known for an important language class there, the LR (k) languages , which is essentially based on this term.
Left derivative
Analogous to the right derivation, one speaks of a left derivation , if the leftmost non-terminal symbol is always replaced.
Left derivatives play a role in the syntax analysis of LL (k) grammars , but since the class of LR (k) grammars, which is more important because of their greater generation power, is based on right derivatives, overall a smaller one. This apparent asymmetry is a consequence of the convention of reading and processing input strings from left to right.
literature
- Alfred V. Aho , Ravi Sethi, Jeffrey D. Ullman : Compilers - Principles, Techniques and Tools (= Addison-Wesley Series in Computer Science. ) Addison-Wesley, Reading MA u. a. 1986, ISBN 0-201-10088-6 , pp. 196-197.
- Arto K. Salomaa: Formal Languages. Springer Verlag, Berlin a. a. 1978, ISBN 3-540-09030-4 .
- Seppo Sippu, Eljas Soisalon-Soininen: Parsing Theory. 2 volumes. Springer Verlag, Berlin a. a. 1988, ISBN 3-540-13720-3 (Volume 1), ISBN 3-540-51732-4 (Volume 2), ( EATCS Monographs on theoretical Computer Science 15 and 20).
Individual evidence
- ^ Robert I. McKay, Nguyen Xuan Hoai, Peter Alexander Whigham, Yin Shan, Michael O'Neill: Grammar-based Genetic Programming: a survey . In: Genetic Programming and Evolvable Machines . tape 11 , no. 3–4 , May 1, 2010, ISSN 1389-2576 , pp. 365-396 , doi : 10.1007 / s10710-010-9109-y .
- ↑ For any two-digit homogeneous relations also called a way : Hans-Rudolf Metz: Relationen ,wege, Hüllen (PDF), FH Gießen-Friedberg, Diskrete Mathematik (Computer Science), SS 2010 - script 16, June 2, 2010 (accessed on 16 April 2018). In the graph-theoretical sense it is a directed path (without edge weights).