Carothers equation

The Carothers equation describes the relationship between the degree of polymerization and the degree of conversion in a step growth reaction . It is named after Wallace Hume Carothers . There are several variants, for linear A – B systems, linear A – A / B – B systems and non-linear step growth reactions. In linear AB systems, there is a monomer in which the monomer carries two functional groups , such as B. at HO-R-COOH. In linear A – A / B – B systems, there are 2 monomers, each with one of the functional groups at both ends, such as B. HOOC – Ph – COOH and HO– (CH ₂ ) ₂ –OH, which can react to form polyethylene terephthalate . In non-linear systems, for. For example, in addition to A – B monomers, there are also trifunctional monomers, which leads to crosslinking of the product. ${\displaystyle \textstyle {\overline {X}}_{n}}$ ${\displaystyle p}$

Linear step growth responses

AB systems

If the number of monomers originally present and the number of molecules still present at the time is ( includes all degrees of polymerization: monomers, oligomers and polymers), the conversion is obtained ${\displaystyle N_{0}}$ ${\displaystyle N_{t}}$ ${\displaystyle t}$ ${\displaystyle N_{t}}$ ${\displaystyle p}$

${\displaystyle p={\frac {N_{0}-N_{t}}{N_{0}}}}$  (1)

p is the probability that one of the groups responded. With a turnover of , the probability that a group has responded is 50%. ${\displaystyle p=0.5}$

The degree of polymerization - the average length of the chains - can be expressed as the fraction of the number of monomers initially present by the molecules still present at time t: ${\displaystyle {\overline {X}}_{n}}$

${\displaystyle {\overline {X}}_{n}={\frac {N_{0}}{N_{t}}}}$   (2)

By transforming Eq. 1

${\displaystyle p={\frac {N_{0}-N_{t}}{N_{0}}}\Leftrightarrow {\frac {N_{0}}{N_{t}}}={\frac {1}{1-p}}}$

and insert in Eq. 2 one obtains the Carothers equation for AB systems

${\displaystyle {\overline {X}}_{n}={\frac {1}{1-p}}}$

AA / BB systems

For AA / BB systems it must also be noted that the system cannot be composed stoichiometrically, i. H. different monomer ratio can occur. That's why you define a parameter : ${\displaystyle r}$

${\displaystyle r={\frac {N_{A}}{N_{B}}}}$

The parameter is always defined so that there is, i.e. there is more BB in the system than AA. ${\displaystyle r<1}$

This gives you as ${\displaystyle N_{0}}$

${\displaystyle N_{0}=N_{A}+N_{B}=rN_{B}+N_{B}}$

At the time , AA molecules have already been converted into turnover . For , the sum of converted AA and BB therefore applies . ${\displaystyle t}$ ${\displaystyle p_{A}}$ ${\displaystyle pN_{A}}$ ${\displaystyle N_{t}}$ ${\displaystyle 2pN_{A}=2rpN_{B}}$

The amount of unreacted monomers is accordingly ${\displaystyle N_{t}}$

${\displaystyle N_{T}=N_{0}-2rpN_{B}=rN_{B}+N_{B}-2rpN_{B}}$

In the same way as above, substituting the following expression for ${\displaystyle {\overline {X}}_{n}}$

${\displaystyle {\overline {X}}_{n}={\frac {N_{0}}{N_{t}}}={\frac {rN_{B}+N_{B}}{rN_{B}+N_{B}-2rpN_{B}}}\Leftrightarrow }$

${\displaystyle {\overline {X}}_{n}={\frac {1+r}{1+r-2pr}}}$

what the Carothers equation for AA / BB-systems corresponding

Nonlinear step growth reactions

AB systems

If trifunctional monomers are added to the monomer , a network is formed.

In order to be able to calculate the degree of polymerization, an average functionality of the monomers is defined

${\displaystyle f={\frac {\sum {N_{i}f_{i}}}{\sum {N_{i}}}}}$

Here, the number of functional groups on the molecule i and the number of monomer molecules. ${\displaystyle f_{i}}$ ${\displaystyle N_{i}}$

In the case of monomer molecules, functional groups are present overall . ${\displaystyle N_{0}}$ ${\displaystyle N_{0}\cdot f}$

After a time t, groups have reacted, since two end groups have to react for a bond. This resulted in the formation of molecules. So the probability of a reaction is ${\displaystyle 2(N_{0}-N_{t})}$ ${\displaystyle (N_{0}-N_{t})}$

${\displaystyle p={\frac {2(N_{0}-N_{t})}{fN_{0}}}}$   (3)

Transforming Eq. 3 results

${\displaystyle 2N_{t}=N_{0}(2-fp)}$

and after insertion in Eq. 2 one obtains a Carothers equation for nonlinear systems

${\displaystyle {\overline {X}}_{n}={\frac {2}{(2-pf)}}}$

Equation 3 can also be transformed

${\displaystyle p={\frac {2}{f}}-{\frac {2}{f{\overline {X}}_{n}}}}$   (4)

When the degree of polymerization approaches infinity, gelation occurs and in Eq. 4 goes the expression

${\displaystyle {\frac {2}{f{\overline {X}}_{n}}}\rightarrow 0}$

The following applies to the turnover where the mixture begins to gel: ${\displaystyle p_{G}}$

${\displaystyle p_{G}={\frac {2}{f}}}$

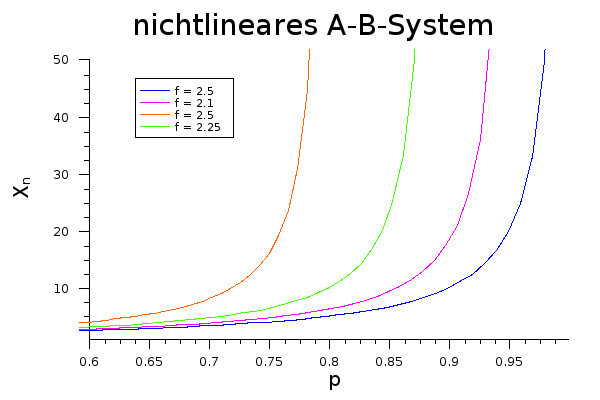
From this relationship it can be seen that a high degree of polymerization can be achieved even with significantly lower conversions than in the other cases.

This equation only applies if the mixture is composed stoichiometrically (same number of A and B groups).

Graphic representation of conversion and degree of polymerization

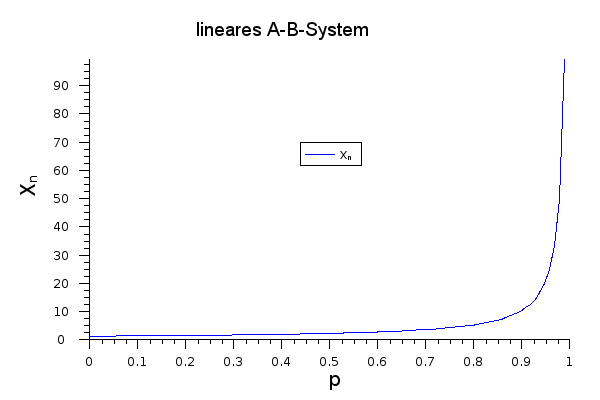
The meaning of the Carothers equation can be seen if the degree of polymerization is plotted against the conversion p: ${\displaystyle {\overline {X}}_{n}}$

Only at very high conversions does the degree of polymerization reach appreciably high values. At p = 0.5 it is just 2, and a value of 10,000 is only achieved at a conversion rate of p = 0.9999.

In the same way, r has a significant influence on the degree of polymerization:

Even small deviations of r from the ideal value 1 mean a significantly lower degree of polymerization.

With the addition of crosslinkers, on the other hand, the conversion increases sharply even at a lower level: ${\displaystyle {\overline {X}}_{n}}$

Individual evidence

1. ^ Polymers: Chemistry and Physics of Modern Material, by John McKenzie, Grant Cowie . books.google.de. Retrieved May 23, 2009.

Web links

• Macromolecules at TU Chemnitz, page 25 (PDF file; 505 kB)