Dieudonné plank

The Dieudonné plank is a special topological space that goes back to the mathematician Jean Dieudonné . It is an example of a metacompact but not countably paracompact space .

Construction of space

The base quantities of the Dieudonné plank

Let it be the first infinite and the first uncountable ordinal number as well as and the corresponding intervals of ordinal numbers. ${\displaystyle \omega }$ ${\displaystyle \Omega }$ ${\displaystyle [0,\omega ]}$ ${\displaystyle [0,\Omega ]}$

The product of the intervals without the "right, upper corner" serves as the base quantity . A topology is explained by defining all ordinal numbers and the following sets as open sets : ${\displaystyle X=[0,\Omega ]\times [0,\omega ]\setminus \{(\Omega ,\omega )\}}$ ${\displaystyle X}$ ${\displaystyle 0\leq \alpha <\Omega }$ ${\displaystyle 0\leq \beta <\omega }$

• the one-point sets , ${\displaystyle \{(\alpha ,\beta )\}}$
• ${\displaystyle U_{\beta }(\alpha )=\{(\alpha ,\gamma )\mid \beta <\gamma \leq \omega \}=\{\alpha \}\times (\beta ,\omega ]}$,
• ${\displaystyle V_{\alpha }(\beta )=\{(\gamma ,\beta )\mid \alpha <\gamma \leq \Omega \}=(\alpha ,\Omega ]\times \{\beta \}}$.

The topological space defined by this base is called the Dieudonné plank .

The underlying amount is the same as that of the Tikhonov plank , but the topology of the Dieudonné plank is finer . ${\displaystyle X}$

properties

The Dieudonné plank is a Hausdorff room

A simple inspection of the open base sets shows that a Hausdorff room is. In fact, it's a completely regular room , but it's not normal . ${\displaystyle X}$

The Dieudonné plank is metacompact

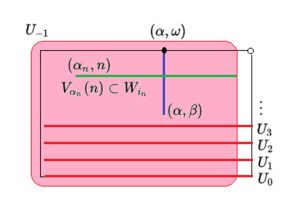
The Dieudonné plank is metacompact, because for every open cover one finds a point refinement by choosing a base set for each point, which is also located in a cover set containing this point. Since each point can lie in at most three different base sets, this refinement is actually point-finite.

The Dieudonné plank is not countable, paracompact

The Dieudonné plank is not paracompact as it is not even normal. But it could be countably paracompact. We show that this is not the case either.

The quantities

• ${\displaystyle U_{-1}:=X\setminus \{(\Omega ,n)|0\leq n<\omega \}}$
• ${\displaystyle U_{n}:=V_{0}(n),\quad n=0,1,2,3,\ldots }$

form a countable open cover of . It has no locally finite refinement, as is an open refinement, so you can at any one found with and this amount must be in one of the sets of lie, because it is a refinement. But since it is the only one containing these quantities , it must be . Because it is also open, according to the definition of the topology there must be a with . Because as a countable union of countable sets it is countable again, it follows . At this point, the choice of is used as the smallest uncountable ordinal number. If there is any environment of , then there is with , and it follows for everyone . So every neighborhood intersects with an infinite number of , that is, is not locally finite. Hence a countable, open cover that has no locally finite, open refinement, that is, is not countable, is paracompact. ${\displaystyle {\mathcal {U}}}$ ${\displaystyle X}$ ${\displaystyle {\mathcal {W}}=(W_{i})_{i\in I}}$ ${\displaystyle 0\leq n<\omega }$ ${\displaystyle i_{n}}$ ${\displaystyle (\Omega ,n)\in W_{i_{n}}}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle U_{n}}$ ${\displaystyle (\Omega ,n)}$ ${\displaystyle U_{n}}$ ${\displaystyle W_{i_{n}}}$ ${\displaystyle 0\leq \alpha _{n}<\Omega }$ ${\displaystyle V_{\alpha _{n}}(n)\subset W_{i_{n}}\subset U_{n}}$ ${\displaystyle \textstyle \alpha :=\sup _{0\leq n<\omega }\alpha _{n}}$ ${\displaystyle \alpha <\Omega }$ ${\displaystyle \Omega }$ ${\displaystyle U}$ ${\displaystyle (\alpha ,\omega )}$ ${\displaystyle 0\leq \beta <\omega }$ ${\displaystyle U_{\beta }(\alpha )\subset U}$ ${\displaystyle U\cap W_{i_{n}}\not =\emptyset }$ ${\displaystyle n\geq \beta }$ ${\displaystyle (\alpha ,\omega )}$ ${\displaystyle W_{i}}$ ${\displaystyle {\mathcal {W}}}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle X}$

Individual evidence

1. ^ J. Dieudonné : Une généralisation des espaces compacts. In: J. Math. Pure Appl. Volume 23, 1944, pp. 65-76.
2. ↑ Lynn Arthur Steen, J. Arthur Seebach: Counterexamples in Topology. Springer-Verlag, 1978, ISBN 3-540-90312-7 , example 89.