Carter triangle

Fuhrmann triangle (red): Arc centers: ${\displaystyle \triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }}$
${\displaystyle M_{a},M_{b},M_{c}}$

Carter triangle (red): ${\displaystyle \triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }}$
${\displaystyle \triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}}$

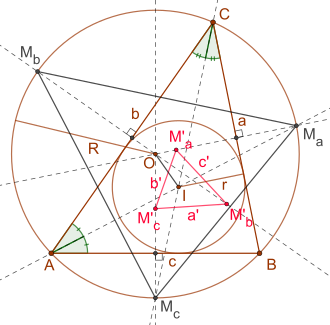
The Fuhrmann triangle , named after Wilhelm Fuhrmann (1833–1904), is a special triangle that is defined by a given starting triangle.

For a given starting triangle , the centers of the circular arcs of the perimeter are above the sides of the triangle . These center points are mirrored on the corresponding sides of the triangle and the mirror points are the corner points of the Fuhrmann triangle . If the given triangle is equilateral, then these three points coincide. ${\displaystyle \triangle ABC}$ ${\displaystyle M_{a},M_{b},M_{c}}$ ${\displaystyle a,b,c}$ ${\displaystyle M_{a}^{\prime },M_{b}^{\prime },M_{c}^{\prime }}$

The perimeter of the carter's triangle is also known as the carter's circle . Furthermore, the Fuhrmann triangle is similar to the triangle formed by the centers of the circular arcs, so and for its area: ${\displaystyle \triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}}$

${\displaystyle |\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }|={\frac {(a+b+c)|OI|^{2}}{4R}}={\frac {(a+b+c)(R-2r)}{4}}}$

Here refers to the center of the circumscribed circle of the initial triangle and its radius, and the center of the inscribed circle and its radius. Based on Euler's theorem, the following also applies to the distance between the two center points . The following equations exist for the side lengths of the Fuhrmann triangle: ${\displaystyle O}$ ${\displaystyle \triangle ABC}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle r}$ ${\displaystyle |OI|^{2}=R(R-2r)}$

${\displaystyle a^{\prime }={\sqrt {\frac {(-a+b+c)(a+b+c)}{bc}}}|OI|}$

${\displaystyle b^{\prime }={\sqrt {\frac {(a-b+c)(a+b+c)}{ac}}}|OI|}$

${\displaystyle c^{\prime }={\sqrt {\frac {(a+b-c)(a+b+c)}{ab}}}|OI|}$

literature

• Roger A. Johnson: Advanced Euclidean Geometry . Dover 2007, ISBN 978-0-486-46237-0 , pp. 228-229, 300 (first published in 1929 by the Houghton Mifflin Company (Boston) under the title Modern Geometry ).
• Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry . MAA, 1995, pp. 49-52

Web links

• Eric W. Weisstein : Carter triangle . In: MathWorld (English).