Koalgebra

This article looks at koalgebras over bodies. For koalgebras over comonads see there.

A koalgebra is a vector space that has a structure that is dual to an algebra. This means that instead of a multiplication that maps two elements to their product, there is a multiplication that maps an element to a tensor product , and instead of a neutral element that enables the basic field to be embedded in the algebra, there is a mapping from the coalgebra into the basic body, which is called Koeins .

definition

A koalgebra over a body is a - vector space with vector space homomorphisms , called multiplication , coproduct or also diagonal , and , called koeins , such that ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle C}$ ${\displaystyle \Delta _{C}\colon C\to C\otimes _{k}C}$ ${\displaystyle \epsilon _{C}\colon C\to k}$

${\displaystyle (\mathrm {id} _{C}\otimes \Delta _{C})\circ \Delta _{C}=(\Delta _{C}\otimes \mathrm {id} _{C})\circ \Delta _{C}}$ (Coassociativity)

${\displaystyle (\mathrm {id} _{C}\otimes \epsilon _{C})\circ \Delta _{C}=\mathrm {id} _{C}=(\epsilon _{C}\otimes \mathrm {id} _{C})\circ \Delta _{C}}$ (Koeins)

A koalgebra homomorphism between two coalgebras C and D is a vector space homomorphism with ${\displaystyle f\colon C\to D}$

${\displaystyle f\otimes f\circ \Delta _{C}=\Delta _{D}\circ f}$and . ${\displaystyle \epsilon _{C}=\epsilon _{D}\circ f}$

example

Be the canonical base of . One can refer to a koalgebra structure by means of ${\displaystyle (e_{1},e_{2},e_{3})}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle \Delta _{\mathbb {R} ^{3}}(e_{i})=e_{i}\otimes e_{i}}$

and

${\displaystyle \epsilon _{\mathbb {R} ^{3}}(e_{i})=1}$

define.

${\displaystyle \Delta _{\mathbb {R} ^{3}}}$ is co-associative, there

${\displaystyle e_{i}\otimes \Delta _{\mathbb {R} ^{3}}(e_{i})=e_{i}\otimes e_{i}\otimes e_{i}=\Delta _{\mathbb {R} ^{3}}(e_{i})\otimes e_{i}}$,

and there is no one ${\displaystyle \epsilon _{\mathbb {R} ^{3}}}$

${\displaystyle e_{i}\otimes \epsilon _{\mathbb {R} ^{3}}(e_{i})=e_{i}=\epsilon _{\mathbb {R} ^{3}}(e_{i})\otimes e_{i}}$.

The elements of are second order tensors and can therefore be represented as matrices. The multiplication is then ${\displaystyle \mathbb {R} ^{3}\otimes \mathbb {R} ^{3}}$

${\displaystyle \Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}=a_{1}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}1\\0\\0\end{pmatrix}}+a_{2}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}0\\1\\0\end{pmatrix}}+a_{3}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}0\\0\\1\end{pmatrix}}={\begin{pmatrix}a_{1}&0&0\\0&a_{2}&0\\0&0&a_{3}\end{pmatrix}}}$.

duality

The multiplication of a (unitary associative) algebra is bilinear, and due to the universal property of the tensor product it can be understood as a mapping from to . The multiplication is associative if and only if the following diagram commutes. ${\displaystyle \mu _{A}}$ ${\displaystyle A}$ ${\displaystyle A\otimes A}$ ${\displaystyle A}$

An algebra has a neutral element if and only if there is a vector space homomorphism , so that the following diagram commutes: ${\displaystyle A}$ ${\displaystyle \eta _{A}}$

In this case . ${\displaystyle 1_{A}=\eta _{A}(1_{k})}$

A koalgebra is an algebra in the category dual to the vector spaces . That is, instead of multiplication there is a mapping so that the following dual diagram commutes: ${\displaystyle C}$ ${\displaystyle \mathrm {Vekt} }$ ${\displaystyle \mathrm {Vekt} ^{\mathrm {op} }}$ ${\displaystyle \Delta _{C}\colon C\to C\otimes C}$

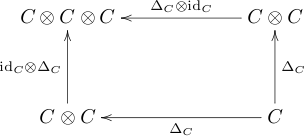
And instead of a neutral element there is a mapping , so the following dual diagram commutes: ${\displaystyle \epsilon _{C}\colon C\to k}$

Sweeder notation

In general, the only known information about the coproduct of an element is that it is in , and thus that it is known as ${\displaystyle \Delta _{C}(x)}$ ${\displaystyle x\in C}$ ${\displaystyle C\otimes C}$

${\displaystyle \Delta _{C}(x)=\sum _{i}x_{(1)}^{(i)}\otimes x_{(2)}^{(i)}}$

can represent. In the Sweedler notation (after Moss Sweedler ) this is abbreviated by symbolically

${\displaystyle \Delta _{C}(x)=\sum _{(x)}x_{(1)}\otimes x_{(2)}}$

writes. In the sumless Sweedler notation you even do without the sum symbol and write

${\displaystyle \Delta _{C}(x)=x_{(1)}\otimes x_{(2)}}$

It is important to note that this notation still denotes a sum. The symbols and are meaningless on their own and are not available for certain elements , because the representation of is not clear. For calculations in the Sweedler notation, one reads the best as "suitable and firmly selected for this calculation" elements. ${\displaystyle x_{(1)}}$ ${\displaystyle x_{(2)}}$ ${\displaystyle C}$ ${\displaystyle \textstyle \Delta _{C}(x)}$ ${\displaystyle \textstyle x_{(k)}^{(i)}}$

This notation enables the composition of functions other than ${\displaystyle \Delta _{C}}$

${\displaystyle (f\otimes g)\circ \Delta _{C}(x)=f(x_{(1)})\otimes g(x_{(2)})}$

to write.

In sumless Sweedler notation, it is Koeins if and only if ${\displaystyle \epsilon _{C}}$

${\displaystyle \epsilon _{C}(x_{(1)})x_{(2)}=x=x_{(1)}\epsilon _{C}(x_{(2)})}$.

The co- product is co-associative if and only if ${\displaystyle \Delta _{C}}$

${\displaystyle x_{(1)}\otimes \Delta _{C}(x_{(2)})=\Delta _{C}(x_{(1)})\otimes x_{(2)}}$.

This element is symbolically represented in Sweedler notation as

${\displaystyle \sum _{(x)}x_{(1)}\otimes x_{(2)}\otimes x_{(3)}}$

and humming as

${\displaystyle x_{(1)}\otimes x_{(2)}\otimes x_{(3)}}$

written.

Applying again results in longer tensor products that are written analogously. You may have to increase the "indices" of the rear elements: ${\displaystyle \Delta _{C}}$

${\displaystyle f(x_{(1)})\otimes \Delta _{C}(x_{(2)})\otimes g(x_{(3)})=f(x_{(1)})\otimes x_{(2)}\otimes x_{(3)}\otimes g(x_{(4)})}$.

By using , the tensor products are shortened, the "indices" of the rear elements are adjusted accordingly: ${\displaystyle \epsilon _{C}}$

${\displaystyle f(x_{(1)})\otimes \epsilon _{C}(x_{(2)})\otimes x_{(3)}\otimes g(x_{(4)})=f(x_{(1)})\otimes x_{(2)}\otimes g(x_{(3)})}$.

literature

• Christian Kassel: Quantum Groups In: Graduate Texts in Mathematics . Springer-Verlag, ISBN 0-387-94370-6 .