Cost function (economy)

This article covers the cost function in economics. For the possibility of estimating the complexity of an algorithm within computer science, see O notation .

The different types of cost trends.

Costs and marginal costs graphically

Cost function and marginal costs in connection with the monopoly price model

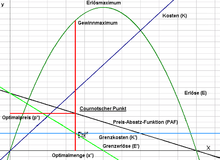
In economics, a cost function represents the relationship between costs and a reference value .

The first derivative of the cost function is called marginal costs .

Types of cost functions

Depending on their course, the following cost functions are distinguished:

proportional (linear)

The costs change in the same proportion as the reference quantity. The unit costs then remain constant - regardless of the reference quantity - and are identical to the marginal costs.

degressive (disproportionately low)

The costs increase more slowly as the reference quantity increases. The unit costs therefore decrease as the output volume increases. This can e.g. B. are due to discounts that are granted in the event of high quantities. Another example would be that the production time decreases due to a learning curve effect, i.e. H. the third pc produced is manufactured faster than the first.

progressive (disproportionate)

The costs increase more with increasing reference quantity. The unit costs increase (e.g. due to overtime ).

regressive (decreasing)

The costs and their unit costs decrease as the reference quantity increases (e.g. heating costs in event rooms when the number of visitors increases).

fix

The costs remain constant regardless of the value of the reference value. The unit cost function is degressive (see also fixed cost degression ). The marginal cost is 0.

sprungfix

The costs remain constant at certain intervals of the reference quantity. Between these intervals the costs “jump” to another level. The cost function assumes a stair-like course .

Reciprocal

The graph runs in an RL-turning curve (reciprocal "s-shaped" / degressive-progressive function) and is a non-linear cost curve as in the picture of the same name (black graph)

overview

Non-linear cost history.

course	general form ${\displaystyle K(x)}$	example	Marginal cost ${\displaystyle K'(x)}$	Unit cost ${\displaystyle k(x)}$
proportional	${\displaystyle c\cdot x}$	${\displaystyle x}$	${\displaystyle c}$	${\displaystyle c}$
degressive	${\displaystyle x^{c \over a}}$	${\displaystyle {\sqrt {x}}}$	${\displaystyle {c \over a}\cdot x^{{c \over a}-1}}$	${\displaystyle x^{{c \over a}-1}}$
progressive	${\displaystyle c\cdot x^{a}}$	${\displaystyle x^{2}}$	${\displaystyle {a\cdot c}\cdot x^{a-1}}$	${\displaystyle c\cdot {x^{a-1}}}$
regressive	${\displaystyle c\cdot x^{-a}}$	${\displaystyle 1 \over x}$	${\displaystyle (-a)\cdot c\cdot x^{-a-1}}$	${\displaystyle c\cdot x^{-a-1}}$
fix	${\displaystyle c}$	${\displaystyle 1000}$	${\displaystyle 0}$	${\displaystyle c \over x}$
sprungfix	${\displaystyle {\begin{cases}a,x<c\\b,c\leq x\leq d\\\ldots ,\ldots \end{cases}}}$	${\displaystyle {\begin{cases}1000,x<50\\2000,50\leq x\leq 200\\5000,x>200\end{cases}}}$	${\displaystyle 0}$, in the jump points ${\displaystyle \infty }$	${\displaystyle {\begin{cases}{a \over x},x<c\\{b \over x},c\leq x\leq d\\\ldots ,\ldots \end{cases}}}$

The following applies here

${\displaystyle K}$: Cost function

${\displaystyle x}$: Reference quantity

${\displaystyle a\in \mathbb {N} _{>1}}$and : constants. This also applies to degressive costs . ${\displaystyle b,c,d\in \mathbb {R} _{>0}}$ ${\displaystyle c<a}$

Explanation of the graphic non-linear cost curve

The total average costs initially decrease because the increased production brings cost advantages. The quantity quantification should best be interpreted as output per unit of time . This could explain why the total average costs temporarily rise again later: Because the production capacity limit is reached, an expansion investment is required, the costs of which are allocated to the total average costs. The fact that the marginal cost curve intersects the average cost curves at their minimum is explained by the fact that as long as the cost increase of the last unit is smaller than the average cost of all previous units, this increase is the average of all previous increases in which it is included presses. As soon as GK = DK, the average can no longer be pressed and will then be increased in the future.

See also

• Revenue function

Web links

Commons : Cost and Income Curves  - Collection of images, videos and audio files

Individual proof

1. ^ PA Samuelson: Economics , Volume 2