Cubic graph
A simple graph in the called graph theory cubic or 3-regular if all its nodes the degrees have third Cubic graphs are therefore regular graphs . Since 1-regular graphs only represent a pairing and 2-regular graphs decompose into disjoint cycles , cubic graphs are the simplest nontrivial cases of regular graphs.
Number of cubic graphs
Since the sum of the node degrees in simple graphs must always be even, cubic graphs always have an even number of nodes .
| n | # Connected cubic graphs with n nodes | # Cubic graphs with n nodes |
|---|---|---|
| 2 | 0 | 0 |
| 4th | 1 | 1 |
| 6th | 2 | 2 |
| 8th | 5 | 6th |
| 10 | 19th | 21st |
| 12 | 85 | 94 |
Examples
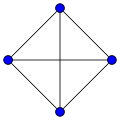
The full graph is the only cubic graph with 4 nodes.
A cubic graph with 6 nodes.
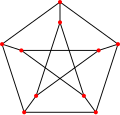
The Petersen graph as an example of a cubic graph.
Web links
Commons : 3-regular graphs - collection of images, videos and audio files
- Weisstein, Eric W .: Cubic Graph . In: MathWorld (English).