Merkle's meta-procedure

Merkle's meta-method (also Merkle-Damgård construction ) is a method for the construction of cryptographic hash functions that goes back to the work of Ralph Merkle and Ivan Damgård .

There is a compression function that maps a bit long input to a bit long output. It is collision-proof , which means that it is not possible with realistic effort to find two different inputs that are mapped to the same output. The application of Merkle's meta-method results in a collision-proof hash function that maps messages of any length to a hash value of bits. ${\displaystyle f\colon \{0,1\}^{a+b}\rightarrow \{0,1\}^{b}}$ ${\displaystyle a+b}$ ${\displaystyle b}$ ${\displaystyle h\colon \{0,1\}^{*}\rightarrow \{0,1\}^{b}}$ ${\displaystyle b}$

method

The hash value is generated from the message blocks by repeatedly using the compression function

The message is first expanded with a padding process so that the length is a multiple of the block size . Then it is divided into blocks of length : ${\displaystyle m}$ ${\displaystyle {\overline {m}}}$ ${\displaystyle {\overline {m}}}$ ${\displaystyle a}$ ${\displaystyle {\overline {m}}}$ ${\displaystyle n}$ ${\displaystyle a}$

${\displaystyle {\overline {m}}=m_{1}\|m_{2}\|\ldots \|m_{n}}$ with . ${\displaystyle |m_{i}|=a}$

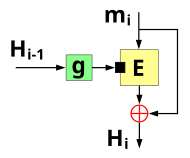
The compression function is iteratively applied to the bit long output of the previous iteration and the next block of the extended message until it is fully processed. In the first iteration, the input consists of a bit long initialization vector , often with the value 0, and the first message block . ${\displaystyle f}$ ${\displaystyle b}$ ${\displaystyle m_{i}}$ ${\displaystyle b}$ ${\displaystyle H_{0}}$ ${\displaystyle m_{1}}$

${\displaystyle H_{i}:=f(H_{i-1}\|m_{i});\quad 1\leq i\leq n}$.

The hash value is then calculated from the last compression output by a finalize function: . The finalization function is often identity or truncation . ${\displaystyle h=\operatorname {final} (H_{n})}$

Davies-Meyer compression function

Matyas – Meyer – Oseas compression function

Block encryption is often used as the compression function, for which there are mainly two options: The Davies-Meyer compression function uses the message block as a key to encrypt the result of the previous compression . Then the cipher text calculated in this way is linked with the plain text (often by bit-wise XOR ). This removes the property of a block cipher to map the plaintext bijectively to the ciphertext, and the mapping from to is much more similar to a random function. Otherwise the compression function would not be collision-proof either, because an attacker could pretend and decrypt with various . ${\displaystyle m_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i}}$ ${\displaystyle H_{i}}$ ${\displaystyle m_{i}}$

The Matyas – Meyer – Oseas compression function encrypts the message block with the previous compression output as the key. Here, too, plain text and key text are then linked. To adapt to the given key length, it may be necessary to expand or compress with a function . ${\displaystyle H_{i-1}}$ ${\displaystyle g}$

Padding

In order for the collision security of the compression function to be verifiably transferred to the hash function, the padding process must meet certain conditions. The following conditions are sufficient for this:

• ${\displaystyle m}$is an initial part of , d. That is, the messages are not changed, just expanded with a tail. ${\displaystyle {\overline {m}}}$
• Two messages of the same length are extended with end pieces of the same length.
• Two messages of different lengths are expanded differently, so that they differ in the last block, which is entered in the last compression level.

Typically, when padding, a coding of the bit length is appended to the message, and bits with the value 0 are inserted in between, so that it is a multiple of the block size : ${\displaystyle \left|m\right|}$ ${\displaystyle |{\overline {m}}|}$ ${\displaystyle a}$

${\displaystyle {\overline {m}}=m\,\|\,0^{k}\,\|\,|m|}$

weaknesses

A weakness is a possible extension attack ( extension Attack ): When the finalize function is reversible, then you can from the hash value of an unknown message the hash easily determine a message from the above enhanced message by adding an extension can be seen. So you can determine hash values ​​for messages that start with, even if you don't know. Since a random oracle does not have this property, it can lead to attacks on processes that only have proof of security in the random oracle model. It also follows from this: once you have found a collision between two messages with the same number of blocks , you can easily determine further collisions by expanding them. ${\displaystyle h(m)}$ ${\displaystyle m}$ ${\displaystyle h({\overline {m}}\,\|\,y)}$ ${\displaystyle y}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle n}$

Finding multiple collisions, i.e. several messages that all have the same hash value, requires little more effort than determining a single collision.

A Herding attack , i.e. finding a suitable ending for a self-selected hash value z and a given beginning part of a message so that the entire message hash to z, i.e. That is, finding one with requires more effort than finding a collision, but much less than should be the case for a random oracle as a hash function . ${\displaystyle m}$ ${\displaystyle y}$ ${\displaystyle h(m\|y)=z}$ ${\displaystyle h}$

An attack to determine a second pre- image attack , in which one searches for a second one with the same hash value for a given message , is possible with a message of the length of blocks with the expenditure of time , and thus considerably faster with long messages than with a systematic one Try (brute force), which requires some steps. ${\displaystyle m}$ ${\displaystyle m^{\prime }}$ ${\displaystyle h(m)=h(m^{\prime })}$ ${\displaystyle 2^{k}}$ ${\displaystyle k2^{b/2+1}+2^{b-k+1}}$ ${\displaystyle 2^{b}}$

Improvements

In order to overcome these weaknesses, Stefan Lucks proposed the wide-pipe-hash construction: To calculate a hash value of bit length, one uses a compression function whose output is longer than , typically twice as long. thus compresses bits from the previous iteration and a bit-long message block into an output of bits. After the last iteration, the output is shortened from to bit by another compression function , if you do not simply discard half the output and use the other half as a hash value. ${\displaystyle b}$ ${\displaystyle f^{\prime }}$ ${\displaystyle b}$ ${\displaystyle f^{\prime }}$ ${\displaystyle 2b}$ ${\displaystyle a}$ ${\displaystyle 2b}$ ${\displaystyle 2b}$ ${\displaystyle b}$

fast wide pipe hash

Nandi and Paul have shown that this construction can be done about twice as fast ( fast wide pipe hash ) by only entering bits from the previous compressions into the next compression, along with a bit long message block . The other half of the compression output is XORed with the following input: ${\displaystyle b}$ ${\displaystyle a+b}$ ${\displaystyle m_{i}}$ ${\displaystyle 2b}$

${\displaystyle h_{i}=f^{\prime }\left(\,(\operatorname {Hi} (h_{i-2})\oplus \operatorname {Lo} (h_{i-1}))\;\|\;m_{i}\right);\quad 1\leq i\leq n-1}$

In the last stage, the output of the penultimate is completely processed, and the message block is only bits wide (unless you use another compression function with a larger input): ${\displaystyle m_{n}}$ ${\displaystyle a}$

${\displaystyle h_{n}=f^{\prime }(\,(\operatorname {Hi} (h_{n-2})\oplus \operatorname {Lo} (h_{n-1}))\;\|\;\operatorname {Hi} (h_{n-1})\;\|\;m_{n})}$

${\displaystyle \operatorname {Hi} (c)}$and mean the first and second half of the bit string . ${\displaystyle \operatorname {Lo} (c)}$ ${\displaystyle c}$

In addition to the wide pipe hash construction, the HAIFA construction is also considered a further development of the Merkle-Damgård method.

Individual evidence

1. ↑ Goldwasser, S. and Bellare, M. "Lecture Notes on Cryptography" . Summer course on cryptography, MIT, 1996-2001.
2. ^ Yevgeniy Dodis, Thomas Ristenpart, Thomas Shrimpton. Salvaging Merkle – Damgård for Practical Applications . Preliminary version in Advances in Cryptology - EUROCRYPT '09 Proceedings, Lecture Notes in Computer Science Vol. 5479, A. Joux, ed, Springer-Verlag, 2009, pp. 371-388.
3. ↑ JS Coron, Y. Dodis, C. Malinaud, and P. Puniya. Merkle – Damgård Revisited: How to Construct a Hash Function. Advances in Cryptology - CRYPTO '05 Proceedings, Lecture Notes in Computer Science, Vol. 3621, Springer-Verlag, 2005, pp. 21-39.
4. ↑ Antoine Joux. Multicollisions in iterated hash functions. Application to cascaded construction. In: Advances in Cryptology - CRYPTO '04 Proceedings, Lecture Notes in Computer Science, Vol. 3152, M. Franklin, ed, Springer-Verlag, 2004, pp. 306-316.
5. ↑ John Kelsey and Tadayoshi Kohno. Herding Hash Functions and the Nostradamus Attack In Eurocrypt 2006, Lecture Notes in Computer Science, Vol. 4004, pp. 183-200.
6. ↑ John Kelsey and Bruce Schneier. Second preimages on n-bit hash functions for much less than 2 ⁿ work. In Ronald Cramer, editor, EUROCRYPT, volume 3494 of LNCS, pages 474–490. Springer, 2005; [1] .
7. ^ S. Lucks, Design Principles for Iterated Hash Functions. In: Cryptology ePrint Archive, Report 2004/253, 2004.
8. ↑ Mridul Nandi and Souradyuti Paul. Speeding Up the Widepipe: Secure and Fast Hashing. In Guang Gong and Kishan Gupta, editor, Indocrypt 2010, Springer, 2010.

literature

• Hans Delfs, Helmut Knebl: Introduction to Cryptography. Springer 2002, ISBN 3-540-42278-1 , p. 40.