Mini float
As Mini Floats are called numbers in a floating point format with just a few bits . Minifloats are not suitable for numerical calculations, but are occasionally used for special purposes or in training.
16-bit minifloats are also known as semi-precise numbers (as opposed to single and double-precision numbers ). There are also minifloats with 8 bits and less. Many minifloats are defined according to the principles of the IEEE-754 standard and contain special values for NaN and infinity. Normalized numbers are then stored with an excess exponent. The revised standard IEEE 754-2008 contains binary minifloats with 16 bits.
The G.711 standard for coding audio data from ITU-T , which is used in audio files of the Au type and for telephone connections, uses 1.3.4 minifloats around a signed 13-bit integer as 8 in the so-called A-law coding -Bit value to represent.
In addition to being used as an exercise format in courses, minifloats are also used in computer graphics to represent whole numbers. If the IEEE 754 principles are used at the same time, the smallest denormalized number must be equal to one. This results in the excess value (bias) to be used. The following example demonstrates the derivation and the underlying principles.
example
A minifloat in one byte (8 bits) with 1 sign bit, 4 exponent bits and 3 mantissa bits (in short: a (1.4.3.-2) number; the brackets contain all IEEE parameters) is intended to represent whole numbers according to IEEE 754- Principles are constructed. Essentially, the bias value must be sensibly determined for this. The (still) unknown exponent (stored value e - bias value b) is temporarily denoted by x. Numbers in other systems are marked with… (): 5 = 101 (2) = 10 (5). The bit pattern is broken down into its components by spaces.
Representation of the zero
0 0000 000 = 0
Denormalized numbers
The mantissa is supplemented with 0.:
0 0000 001 = 0.001(2) * 2^x = 0.125 * 2^x = 1 (kleinste denormalisierte Zahl) ... 0 0000 111 = 0.111(2) * 2^x = 0.875 * 2^x = 7 (größte denormalisierte Zahl)
Normalized numbers
The mantissa is completed with 1.:
0 0001 000 = 1.000(2) * 2^x = 1 * 2^x = 8 (kleinste normalisierte Zahl) 0 0001 001 = 1.001(2) * 2^x = 1.125 * 2^x = 9 ... 0 0010 000 = 1.000(2) * 2^(x+1) = 1 * 2^(x+1) = 16 = 1.6e1 0 0010 001 = 1.001(2) * 2^(x+1) = 1.125 * 2^(x+1) = 18 = 1.8e1 ... 0 1110 000 = 1.000(2) * 2^(x+13) = 1.000 * 2^(x+13) = 65536 = 6.5e4 0 1110 001 = 1.001(2) * 2^(x+13) = 1.125 * 2^(x+13) = 73728 = 7.4e4 ... 0 1110 110 = 1.110(2) * 2^(x+13) = 1.750 * 2^(x+13) = 114688 = 1.1e5 0 1110 111 = 1.111(2) * 2^(x+13) = 1.875 * 2^(x+13) = 122880 = 1.2e5 (größte Normalisierte Zahl)
(The representations on the right take the accuracy into account, because of course you cannot store five or six digits with three bits.)
Infinite
0 1111 000 = unendlich
The numerical value of infinity would be without the IEEE 754 interpretation
0 1111 000 = 1.000(2) * 2^(x+14) = 2^17 = 131072 = 1.3e5 (numerischer Wert von unendlich)
Do not pay
0 1111 xxx = NaN
The numerical value would be the largest NaN without the IEEE 754 interpretation
0 1111 111 = 1.111(2) * 2^(x+14) = 1.875 * 2^17 = 245760 = 2.5e5 (numerischer Wert von NaN)
Derivation
If the smallest denormalized number is to be equal to one, then x = 3 after the second line. This results in an exponent bias (excess value) of −2. From the stored exponent, −2 must be subtracted (+2 added) in order to arrive at the arithmetical exponent x.
Discussion of this example
The advantage of such integer minifloats in one byte is the much larger range of values from −122880 ... 122880 compared to representations in two's complement with −128 ... 127. The accuracy drops rapidly because there are always only 4 significant bit positions. The gaps in the area of the largest normalized numbers are correspondingly large.
This minifloat representation can only represent 242 different numbers (if one regards +0 and −0 as different), since there are 14 different bit patterns that do not represent a number (NaN).
The correspondence of the bit patterns of minifloat numbers and integer numbers between 0 and 16 is interesting. Only the bit pattern 00010001 is interpreted as minifloat 18, but as integer number 17.
However, this correspondence is no longer correct for negative numbers, since negative integers are usually represented in two's complement .
The (vertical) real number axis on the right side of the graphic clearly shows the varying density of floating point numbers - a characteristic of all floating point systems. This varying density determines the graph's exponential function-like course.
Although many computer scientists emotionally believe that the curve can be continuously differentiated, one can clearly see the "kinks" at the points where the exponent value changes. As long as the exponent remains constant, the floating point numbers represented only by different mantissas are even distributed linearly - the curve is a straight line between two "kinks". Of course, there isn't even a curve, since floating point numbers are just a discrete, finite set of points. The statement therefore relates to a curve interpolated as well as possible by the finite point set. In practice there are usually so many points that they look like a continuous curve to the viewer (with double it is 2 64 , i.e. about 10 19 points).
Arithmetic with mini floats
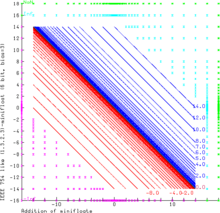
addition
The graphic demonstrates the addition of two even smaller (1.3.2.3) mini floats with 6 bits each. This model represents real numbers according to all IEEE-754 principles. A NaN operand or the calculation “Inf - Inf” result in a NaN result. Inf can be increased or decreased without change (with finite values). Finite sums can also have infinite results (14.0 + 3.0). The finite range (operands and result are finite) is represented by the lines with x + y = c, where c is always one of the representable minifloat values.
Subtraction, multiplication and division
The remaining arithmetic operations can be represented similarly:
As with all multiplications with floating point numbers, approx. 25 percent of the results cannot be represented in the number format of the operands.
Web links
- https://www.khronos.org/registry/OpenGL/extensions/ARB/ARB_half_float_pixel.txt Minifloats for graphic purposes with 16 bit
Individual evidence
- ↑ IEEE 754-2008: Standard for Floating-Point Arithmetic, IEEE Standards Association, 2008, doi : 10.1109 / IEEESTD.2008.4610935