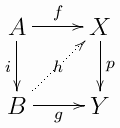Model category

In mathematical homotopy theory , a model category is a category with selected subclasses of arrows called "weak equivalences", "fibers" and "cofibers". The requirements for these classes represent an abstraction of the corresponding topological terms and enable the construction of an associated homotopy category not only for the category of topological spaces , but also for the category of chain complexes . In the latter case, the associated homotopy categories are called derived categories .

The term was introduced in 1967 by Daniel G. Quillen .

definition

In one category , three sub-categories of the same object are distinguished: ${\ displaystyle {\ mathcal {C}}}$

weak equivalences
Fibers
Cofibers.

We call (co-) fibers acyclic or trivial if they are also weak equivalences.

${\ displaystyle {\ mathcal {C}}}$ is called a model category if the following axioms are fulfilled:

MC1 ((co-) limits)

${\ displaystyle {\ mathcal {C}}}$ is finally bi-complete.

MC2 ("2 of 3")

If arrows are in and two of them are weak equivalences, so also the third. ${\ displaystyle f, g, gf}$ ${\ displaystyle {\ mathcal {C}}}$

MC3 (retracts)

If the retract of an arrow belongs to one of the marked subcategories, then it belongs to the same subcategory. ${\ displaystyle f}$ ${\ displaystyle g}$ ${\ displaystyle f}$

MC4 (elevation)

Are on the commutative diagram

${\ displaystyle i}$ Cofiber, fiber and or acyclic, there is an arrow that commutes with the diagram. ${\ displaystyle p}$ ${\ displaystyle i}$ ${\ displaystyle p}$ ${\ displaystyle h \ colon B \ to X}$

MC5 (disassembly)

1. Each arrow can be represented as a grain and acyclic grain . ${\ displaystyle p \ circ i}$ ${\ displaystyle p}$ ${\ displaystyle i}$

2. Each arrow can be represented as for acyclic grain and a cofiber . ${\ displaystyle p \ circ i}$ ${\ displaystyle p}$ ${\ displaystyle i}$

properties

The definition is self-dual: the dual category also has the structure of a model category in which only the classes of fibers and cofibers are interchanged.

{\ displaystyle {\ mathcal {C}} ^ {op}}

The axiom MC4 characterizes the classes of fiberings and Kofaserungen: An arrow is precisely then fibrillation, if for every graph in which is acyclic Cofibration, an elevation is (corresponding to Kofaserungen). A model category structure is therefore already clearly defined by specifying the weak equivalences and one of the classes of fibers and cofibers. ${\ displaystyle p}$ ${\ displaystyle i}$ ${\ displaystyle h}$

The class of fibers is stable when changing the base , that of the fibers is stable when changing the base.

Fibrous and cofibrous objects

In particular, after MC1 contains a start object and an end object . An object is fraying when fibrillation is kofasernd when Cofibration is. ${\ displaystyle {\ mathcal {C}}}$ ${\ displaystyle \ emptyset}$ ${\ displaystyle *}$ ${\ displaystyle X}$ ${\ displaystyle X \ to *}$ ${\ displaystyle \ emptyset \ to X}$

Examples

Topological spaces

The following model category structure is usually considered for the category of topological spaces : The weak homotopy equivalences are selected as weak equivalences , and the Serre fibers are selected as fibers . ${\ displaystyle Top}$

The topological spaces can also be provided with a model structure in which the weak equivalences are the homotopy equivalences.

Chain complexes

The category of chain complexes of R modules with non-negative indices has the following model category structure: ${\ displaystyle Ch_ {R}}$

The arrows (i.e. degree-preserving homomorphisms that respect the derivative operator) that induce isomorphisms in the homology are chosen as weak equivalences.

Fibers are the arrows , the components of which are monomorphisms with a projective coke core for each degree . ${\ displaystyle f}$ ${\ displaystyle f_ {d}}$ ${\ displaystyle d \ geq 0}$

Co-fibers are the arrows for which those in positive degrees are surjective.

{\ displaystyle f}

{\ displaystyle f_ {d}}

{\ displaystyle d> 0}

Homotopy category

In order to be able to transfer the term homotopy to any model category, cylinder objects and path objects are defined, with the help of which left and right homotopies are defined.

These two homotopy terms are in general neither equivalence relations nor do they agree with each other. In the event that the sources and targets of the arrows under consideration are fraying and cofibering, both definitions describe the same equivalence relation. One can therefore move on to a homotopy category as follows: First arrows are functionally replaced by arrows that differ only by weak equivalences, but have fiber and cofiber sources and destinations. Then equivalence classes of left or right homotopic arrows can be combined into homotopy classes and the homotopy category is obtained.

Since the transition to the homotopy category can also be described as a localization with regard to the weak equivalences, no knowledge of the fibers and cofibers is required for the construction of the homotopy category.

literature

WG Dwyer and J. Spalinski: Homotopy Theories and model categories (PDF file; 419 kB), 1995
Mark Hovey: Model Categories , 1999, ISBN 0-8218-1359-5
Daniel G. Quillen: Homotopical algebra , Lecture Notes in Mathematics, vol. 43, Springer-Verlag, 1967.
JP May, J. Sigurdsson: Parametrized Homotopy Theory , 2006 [1] , ISBN 0-8218-3922-5
Ken-ichi Maruyama, John W. Rutter: Groups of Homotopy Self-Equivalences and Related Topics , 2001 [2] , ISBN 0821826832
Alejandro Adem, Samuel Gitler, R. James Milgram, Douglas C. Ravenel: Homotopy Theory and Its Applications , Contemporary Mathematics, Volume: 188, American Mathematical Society, 1995 [3] , ISBN 0821803050 .
Simon Salamon, Brian Steer, Wilson Alexander Sutherland: Advances in Homotopy Theory , Cambridge University Press, 1989 [4] , ISBN 0521379075 .