OPTICS
OPTICS ( English Ordering Points To Identify the Clustering Structure , arrange [about] points to identify the cluster structure ' ) is a dense-based algorithm for cluster analysis . It was developed by Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel and Jörg Sander. The basic principle of the algorithm comes from DBSCAN , but the algorithm solves an important weakness of the DBSCAN algorithm: in contrast to it, it can recognize clusters of different densities. At the same time, it (largely) eliminates the parameter of the DBSCAN algorithm. For this purpose, OPTICS arranges the points of the data set linearly in such a way that spatially adjacent points follow one another in this order. At the same time, the so-called "reachability distance" is noted. If you draw these accessibility distances in a diagram, clusters form “valleys” and can thus be identified.
Core idea
Like DBSCAN, OPTICS uses two parameters, and . However, here it plays the role of a maximum distance and serves primarily to limit the complexity of the algorithm. Substituting , then the complexity of the algorithm , otherwise they can with the help of appropriate spatial indexing structures such as R * tree to be reduced. Without this optimization, however, the complexity remains at finite .
In DBSCAN a point is a “core point” if its surroundings contain at least points. In OPTICS, on the other hand, it is checked when a point would be a key point. This is implemented with the "core distance", ie the value from which a point in DBSCAN would be a "core point". If there is no point with which a point would be a core point, its core distance is infinite or “undefined”.
The “reachability distance ” of a point from a second point is defined as , i.e. as the maximum of the real distance and the core distance of the referring point.
OPTICS now arranges the objects in the database by starting at any unprocessed point, determining the neighbors in the area and memorizing them in a priority queue according to their best reachable distance so far . The point that has the smallest reachable distance is now always included next in the order. By processing a new point, the reachability distances of the unprocessed points can be improved. By sorting this priority queue, OPTICS processes a detected cluster completely before continuing with the next cluster.
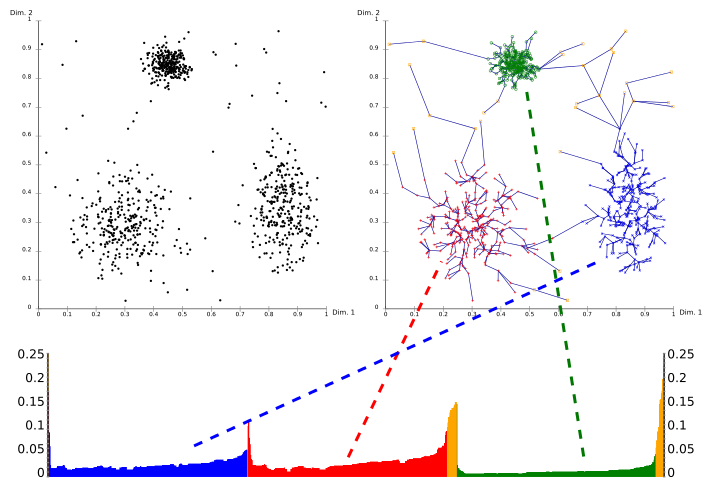
Visualization
OPTICS can be visualized as an accessibility diagram (below). The reachability distance is plotted on the y-axis, the points along the x-axis are sorted according to the order calculated by OPTICS. "Valleys" in this diagram correspond to recognized clusters in the data set; the depth of the valley indicates the density of the cluster. As an additional visualization, here (top right) each point is linked to its predecessor accessibility. The resulting spanning tree visualizes the density connection of the points in the data set determined by OPTICS. Here and were used as parameters . This visualization was created with the OPTICS implementation in ELKI .
Pseudocode
The basic approach of OPTICS is similar to that of DBSCAN , but instead of maintaining a set of "known but not yet processed" objects, these are managed in a priority queue (for example an indexed heap ).
OPTICS(DB, eps, MinPts)
for each point p of DB
p.reachability-distance = UNDEFINED
for each unprocessed point p of DB
N = getNeighbors(p, eps)
mark p as processed
output p to the ordered list
Seeds = empty priority queue
if (core-distance(p, eps, Minpts) != UNDEFINED)
update(N, p, Seeds, eps, Minpts)
for each next q in Seeds
N' = getNeighbors(q, eps)
mark q as processed
output q to the ordered list
if (core-distance(q, eps, Minpts) != UNDEFINED)
update(N', q, Seeds, eps, Minpts)
In update () the priority queue is updated with the environment of or :
update(N, p, Seeds, eps, Minpts)
coredist = core-distance(p, eps, MinPts)
for each o in N
if (o is not processed)
new-reach-dist = max(coredist, dist(p,o))
if (o.reachability-distance == UNDEFINED) // o is not in Seeds
o.reachability-distance = new-reach-dist
Seeds.insert(o, new-reach-dist)
else // o in Seeds, check for improvement
if (new-reach-dist < o.reachability-distance)
o.reachability-distance = new-reach-dist
Seeds.move-up(o, new-reach-dist)
OPTICS outputs the points in a certain order, annotated with their smallest reachable distance (the published algorithm also saves the core distance, but it is no longer required).
Extensions
OPTICS-OF is an OPTICS-based procedure for outlier detection . An important advantage here is that clusters can be determined in the course of a normal OPTICS run without having to carry out a separate outlier detection.
DeLiClu, Density-Link-Clustering combines ideas of single-linkage clustering and OPTICS, thus eliminating the parameter and achieving improved performance compared to OPTICS by using an R-tree as an index.
HiSC is a hierarchical (axis-parallel) subspace clustering method.
HiCO is a hierarchical clustering procedure for any oriented sub-spaces.
DiSH is an improvement of HiSC for more complex hierarchies (with cuts from sub-spaces).
Availability
A reference implementation is available in the chair's software package ELKI , including implementations of DBSCAN and other comparison methods.
The " scikit-learn " module contains an implementation of OPTICS in Python since version scikit-learn v0.21.2.
Individual evidence
- ↑ Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel , Jörg Sander: OPTICS: Ordering Points To Identify the Clustering Structure . In: ACM SIGMOD international conference on Management of data . ACM Press, 1999, pp. 49-60 ( CiteSeerX ).
- ↑ Martin Ester, Hans-Peter Kriegel , Jörg Sander, Xiaowei Xu: A density-based algorithm for discovering clusters in large spatial databases with noise . In: Evangelos Simoudis, Jiawei Han, Usama M. Fayyad (Eds.): Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96) . AAAI Press, 1996, ISBN 1-57735-004-9 , pp. 226-231 ( CiteSeerX ).
- ^ Markus M. Breunig, Hans-Peter Kriegel , Raymond T. Ng and Jörg Sander: Principles of Data Mining and Knowledge Discovery . Springer, 1999, ISBN 978-3-540-66490-1 , OPTICS-OF: Identifying Local Outliers, p. 262-270 , doi : 10.1007 / b72280 ( metapress.com ).
- ↑ E. Achtert, C. Böhm, P. Kröger: DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking . 2006, p. 119 , doi : 10.1007 / 11731139_16 .
- ↑ E. Achtert, C. Böhm, Hans-Peter Kriegel , P. Kröger, I. Müller-Gorman, A. Zimek: Finding Hierarchies of Subspace Clusters . 2006, p. 446 , doi : 10.1007 / 11871637_42 .
- ↑ E. Achtert, C. Böhm, P. Kröger, A. Zimek: Mining Hierarchies of Correlation Clusters . 2006, p. 119 , doi : 10.1109 / SSDBM.2006.35 .
- ↑ E. Achtert, C. Böhm, Hans-Peter Kriegel , P. Kröger, I. Müller-Gorman, A. Zimek: Detection and Visualization of Subspace Cluster Hierarchies . 2007, p. 152 , doi : 10.1007 / 978-3-540-71703-4_15 .
- ↑ sklearn.cluster.OPTICS - scikit-learn 0.21.2 documentation. Retrieved July 3, 2019 .