Orthogonal axonometry

orthogonal axonometry: incision technique

Example: house with incision method (orth. Axonom.)

The orthogonal (vertical) axonometry offers a relatively simple method to produce an orthogonal parallel projection of an object from two assigned cracks (ground plan and elevation) . A cutting method is used for which the images of the coordinate axes can still be (almost) freely selected, but the orientations of the floor plan and elevation are already fixed with this selection (see below). The advantages of orthogonal axonometry are a) good image effect, b) freely selectable projection direction, c) the outline of a sphere is a circle d) fast incision process: You don't have to shorten and mark individual coordinates. It is sufficient to draw parallels to the incision directions and to intersect assigned rays.

Description of the procedure

One assumes a floor plan in the xy plane and an elevation in the yz plane .

1. Select the images of the 3 coordinate axes in the image table (drawing plane) (not all on a straight line).
2. On one of the axes, e.g. B. x-axis, one chooses a point as the track point of the image table, z. B. and constructs the track points taking into account that the images of the coordinate axes are the heights in the track point triangle. (The image of the origin of coordinates is the point of intersection.) ${\displaystyle S_{x}}$ ${\displaystyle S_{y},S_{z}}$
3. The intersection of the Thales circle above with the image of the z-axis provides the zero point of the floor plan rotated into the image table . By pulling out the folded floor plan in the direction of the image of the z-axis (1st incision direction), the position of the floor plan for the subsequent incision procedure results. ${\displaystyle S_{x},S_{y}}$ ${\displaystyle {\tilde {O}}'}$
4. The same procedure is used to determine the position of the elevation for the incision process.
5. Carrying out the incision procedure.

Justification of the procedure

Orthogonal axonometry: position of the floor plan for the incision method

An orthogonal parallel projection is clearly defined by specifying the projection direction. The image board is perpendicular to the direction of projection and can be moved as desired along the direction of projection. In order to obtain a clear image of the three-dimensional object, a direction of projection that is not parallel to one of the coordinate axes is chosen. So the 3 coordinate axes intersect the table in track points , the track point triangle. With the choice of a track point the remaining two are fixed. The images of the coordinate axes are the heights of the track point triangle and the image of the coordinate origin is the intersection of these heights. When the floor plan level (xy level) is folded over around the straight track , the image of the zero point moves into the point on the axis . The track points remain unchanged during the turning process. So the straight line is through the x-axis folded into the table. The folded y-axis and thus the undistorted floor plan plane (xy plane) are obtained in the same way. In order not to disturb the picture to be drawn, pull the floor plan down in the direction of the axis. Proceed in the same way with the elevation (yz plane). The incision directions important for the incision process are the directions of the -axis and -axis. ${\displaystyle \mathbf {p} }$ ${\displaystyle S_{x},S_{y},S_{z}}$ ${\displaystyle S_{x}S_{y}}$ ${\displaystyle {\overline {O}}}$ ${\displaystyle {\overline {z}}}$ ${\displaystyle {\tilde {O}}'}$ ${\displaystyle S_{x}S_{y}}$ ${\displaystyle S_{x},{\tilde {O}}'}$ ${\displaystyle {\overline {z}}}$ ${\displaystyle {\overline {z}}}$ ${\displaystyle {\overline {x}}}$

Sphere and circle

Ellipse: Point construction using the vertex circles

orthogonal axonometry: sphere and cylinder

Spheres are particularly easy to map in orthogonal axonometry: The outline of a sphere is a circle with the radius of the sphere. In order to depict a sphere, you only have to determine the image of the center of the sphere and then draw the outline. In an oblique parallel projection, the outline of a sphere is always an ellipse, the axes of which must first be laboriously determined.

The parallel projection of a circle that is parallel to the picture board is an undistorted circle. In every other case a circle is mapped onto an ellipse , the center of which is the image of the center of the circle. The directions of the main axes and the size of the semi-axes must i. a. can be determined with the Rytz construction .

In the case of an orthogonal parallel projection, that diameter of a circle that is parallel to the image table is mapped undistorted onto the large main axis of the image ellipse. I.e. The center, the main axis directions and the major semi-axis (= circle radius) are known in the picture. The size of the small semiaxis is determined according to the figure "Ellipse: point construction with the help of the vertex circles", by assuming knowledge of the major axis and an ellipse point. In the example, the bottom and top circles of a cylinder are parallel to the xy plane. Straight lines in the xy plane that are parallel to the image table are all parallel to the straight track . So the diameter of the ground circle, which is parallel to this straight track, is shown undistorted. The circle point on the x-axis is used here as the elliptical point for the construction of the small semi-axis. The image of the top circle of the cylinder is the image of the bottom circle shifted into the top. ${\displaystyle S_{x}S_{y}}$

Alternative specifications

orthogonal axonometry: specification of the projection direction

Instead of the above specification of the axis images, you can also

• specify the track point triangle. The axis images are then the heights of this triangle and the image of the coordinate origin is the height intersection.
• the projection direction pretend in ground plan and elevation (see Fig.). For the construction of the tracking point triangle one chooses any point of the x-axis as . Since the track has to run vertically , this results in the intersection of the perpendicular from on with the y-axis in the plan. With the analogous argument in the elevation one finds (see picture). The lengths of the sides and can be seen in the floor plan or elevation. The length of results from turning parallel to the elevation plane (see true length ). This means that all side lengths of the tracking point triangle are known and the triangle can be drawn. (The numbers in the drawing indicate the order of construction steps.) ${\displaystyle \mathbf {p} }$ ${\displaystyle S_{x}}$ ${\displaystyle S_{x}S_{y}}$ ${\displaystyle \mathbf {p} '}$ ${\displaystyle S_{y}}$ ${\displaystyle S_{x}}$ ${\displaystyle \mathbf {p} '}$ ${\displaystyle S_{z}}$ ${\displaystyle S_{x}S_{y}}$ ${\displaystyle S_{y}S_{z}}$ ${\displaystyle S_{x}S_{z}}$

Reversal of the procedure

If one assumes an image in orthogonal parallel projection in which the images of the axes are recognizable, then the inverse of the above incision process can be used to reconstruct the ground plan and elevation . The direction of projection can also be seen in the reconstruction.

Example: reconstruction of an elevation

Reconstruction of an elevation of a cross vault given in orthogonal axonometry. (red: track triangle)

Given: orthogonal axonometry of a cross vault .
Wanted: an elevation to determine the true dimensions.

Solution steps:

1. Selection of a track point: here the center of the right edge circle.
2. Completion of the track triangle (red, see above)
3. Pull out the right elevation: a) Parallel to the right side of the triangle, associated trace points, Thales circle. b) Section of the Thales circle with the associated straight line through the origin. c) Draw the elevation axes.
4. Reconstruction of essential points (see drawing).

Possible shortenings

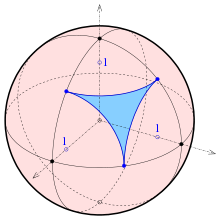
With an orthogonal axonometry, in contrast to a general axonometry , not arbitrary shortenings can occur. One can easily see (see above) that all shortenings are less than or equal . But not any three numbers less than or equal can appear as truncations. To determine which triples are possible, the abbreviations for any orthogonal axonometry are determined: ${\displaystyle v_{x},v_{y},v_{z}}$ ${\displaystyle 1}$ ${\displaystyle 1}$

Let the image table contain the zero point of the coordinate system and the negative projection direction (unit normal of the image plane) be described by the position vector of a point on the unit sphere . The projection can be described as follows: ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {x}}\ \rightarrow {\vec {x}}-({\vec {x}}\cdot {\vec {n}}){\vec {n}}\quad }$ With

${\displaystyle {\vec {n}}=(\cos u\cos v,\sin u\cos v,\sin v)^{T}\ ,\quad 0\leq u,v\leq \pi /2\ .}$

The angles can be thought of as longitude or latitude. The normal vectors lie in the 1st octant of the unit sphere. ${\displaystyle u,v}$

Orthogonal axonometry: possible abbreviations are the coordinates of the blue spherical points

Images of the axes and basis vectors
(here: for is ) ${\displaystyle u=v=30^{\circ }}$ ${\displaystyle \alpha =131^{\circ },\beta =106^{\circ }}$

The pictures of the basis vectors are: ${\displaystyle {\vec {e}}_{1}=(1,0,0)^{T},{\vec {e}}_{2}=(0,1,0)^{T},{\vec {e}}_{3}=(0,0,1)^{T}}$

${\displaystyle {\vec {f}}_{i}={\vec {e}}_{i}-({\vec {e}}_{i}\cdot {\vec {n}})\;{\vec {n}}\ ,\ i=1,2,3\ .}$

Their lengths are the axonometric shortenings: ${\displaystyle {\sqrt {({\vec {e}}_{i}-({\vec {e}}_{i}\cdot {\vec {n}})\;{\vec {n}})^{2}}}={\sqrt {1-(e_{i}\cdot {\vec {n}})^{2}}}}$

• ${\displaystyle v_{x}={\sqrt {1-(\cos u\cos v)^{2}}},\quad v_{y}={\sqrt {1-(\sin u\cos v)^{2}}},\quad v_{z}=\cos v\ }$

From this it follows

• ${\displaystyle v_{x}^{2}+v_{y}^{2}+v_{z}^{2}=2\ ,\quad v_{x},v_{y},v_{z}\leq 1.}$

Only those shortenings are possible that are the coordinates of points on the sphere and lie there within the circular triangle described by (see picture). ${\displaystyle \ x^{2}+y^{2}+z^{2}=2\ }$ ${\displaystyle \ x=1,\;y=1,\;z=1\ }$

In order to determine the angle between the images of the 1st and 3rd or 2nd and 3rd basic vector, one needs ${\displaystyle \alpha ,\beta }$

${\displaystyle {\vec {f}}_{i}\cdot {\vec {f}}_{k}=-({\vec {e}}_{i}\cdot {\vec {n}})({\vec {e}}_{k}\cdot {\vec {n}})\ ,\quad i\neq k\ .}$

It is

${\displaystyle \cos \alpha ={\frac {-({\vec {e}}_{1}\cdot {\vec {n}})({\vec {e}}_{3}\cdot {\vec {n}})}{v_{x}v_{z}}}={\frac {-\cos u\sin v}{\sqrt {1-(\cos u\cos v)^{2}}}}\ ,\ }$

${\displaystyle \cos \beta ={\frac {-({\vec {e}}_{2}\cdot {\vec {n}})({\vec {e}}_{3}\cdot {\vec {n}})}{v_{y}v_{z}}}={\frac {-\sin u\sin v}{\sqrt {1-(\sin u\cos v)^{2}}}}\ .}$

Engineering axonometry

For the Ingenieuraxonometrie is . Inserting into the spherical equation yields and from it ${\displaystyle \ v_{y}=v_{z}=2v_{x}\ }$
${\displaystyle \ {\tfrac {v_{z}^{2}}{4}}+v_{z}^{2}+v_{z}^{2}=2}$

• ${\displaystyle v_{z}={\frac {2{\sqrt {2}}}{3}}=v_{y},\quad v_{x}={\frac {\sqrt {2}}{3}}\ .}$

From follows ${\displaystyle \ v_{z}={\tfrac {2{\sqrt {2}}}{3}}=\cos v\ }$ ${\displaystyle \ v=19,47^{\circ }\ .}$

From and results in and . So is ${\displaystyle \ {\tfrac {8}{9}}=v_{y}^{2}=1-(\sin u\cos v)^{2}\ }$ ${\displaystyle \ \cos ^{2}v={\tfrac {8}{9}}\ }$ ${\displaystyle \ \sin ^{2}u={\tfrac {1}{8}}\;}$ ${\displaystyle \ u=20,7^{\circ }\ }$

${\displaystyle {\vec {n}}=({\tfrac {\sqrt {7}}{3}},{\tfrac {1}{3}},{\tfrac {1}{3}})^{T}\;,}$

${\displaystyle {\vec {f}}_{1}=-{\frac {1}{9}}(-2,{\sqrt {7}},{\sqrt {7}})^{T}\;,\quad {\vec {f}}_{2}=-{\frac {1}{9}}({\sqrt {7}},-8,1)^{T}\;,\quad {\vec {f}}_{3}=-{\frac {1}{9}}({\sqrt {7}},1,-8)^{T}\ .}$

${\displaystyle \cos \alpha =-{\frac {\sqrt {7}}{4}}\quad \to \quad \alpha =131,41^{\circ }\quad ,}$

${\displaystyle \cos \beta =-{\frac {1}{9}}\qquad \to \quad \beta =97,18^{\circ }\quad .}$

In order to achieve the abbreviations customary for engineering axonometry, a scaling with the factor must be added to the orthogonal projection . (Scaling does not change the angles .) ${\displaystyle v_{x}=0.5,v_{y}=v_{z}=1}$ ${\displaystyle {\tfrac {3}{2{\sqrt {2}}}}=1,06}$ ${\displaystyle u,v}$

Isometry

The following applies to an isometry . Inserting into the sphere equation yields ${\displaystyle \;v_{x}=v_{y}=v_{z}\;}$

• ${\displaystyle v_{x}=v_{y}=v_{z}={\sqrt {\tfrac {2}{3}}}\ .}$

If you put this result in the equations for the reductions, you get and with it . The projection angles are ${\displaystyle \cos v={\sqrt {\tfrac {2}{3}}}}$ ${\displaystyle \cos u={\tfrac {1}{\sqrt {2}}}}$

${\displaystyle u=45^{\circ }\;,\ v=35,26^{\circ }\ .}$

So is

${\displaystyle {\vec {n}}={\frac {1}{\sqrt {3}}}(1,1,1)\ ,}$

${\displaystyle {\vec {f}}_{1}={\frac {1}{3}}(2,-1,-1)\;,\ {\vec {f}}_{2}={\frac {1}{3}}(-1,2,-1)\;,\ {\vec {f}}_{3}={\frac {1}{3}}(-1,-1,2)\ }$ and

${\displaystyle \alpha =\beta =120^{\circ }\ .}$

The standard isometry with results when you combine the orthogonal projection with a scaling with the factor . ${\displaystyle \;v_{x}=v_{y}=v_{z}=1\;}$ ${\displaystyle \;{\sqrt {\tfrac {3}{2}}}=1,22\;}$

Individual evidence

1. ↑ EL boots : textbook of descriptive geometry. Springer-Verlag, Basel 1947, ISBN 978-3-0348-4098-9 , p. 40.

literature

• Fucke, Kirch, Nickel: Descriptive Geometry. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4
• Cornelie Leopold : Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X

Web links

• Normal (orthogonal) axonometry with simple examples
• Descriptive geometry for architects (PDF; 1.5 MB). Script (Uni Darmstadt), p. 42