Parallel all-pair shortest paths algorithms

Parallel all-pair shortest paths algorithms are algorithms in graph theory to find the shortest paths between two nodes. Finding the shortest paths between all nodes in a graph is called the all-pairs-shortest-path problem. Since large graphs lead to long runtimes in sequential algorithms that solve this problem, it is worthwhile to parallelize them. Techniques for parallelization for the most popular algorithms and their effects on runtimes are presented here.

Problem Description

Let be a directed graph with the node set and the edge set . A weight is assigned to each edge . The aim is to determine the shortest paths from all nodes to every other node. For this to be clear, it is necessary that there are no negative cycles. ${\displaystyle G=(V,E,w)}$ ${\displaystyle V}$ ${\displaystyle E\subseteq V\times V}$ ${\displaystyle e\in E}$ ${\displaystyle w(e)}$ ${\displaystyle G}$

In the following, we assume that the graph is available in the form of an adjacency matrix at the beginning of the algorithms. As a result of the algorithms we expect the distance matrix , whose entries contain the weight of the shortest path from node to node . ${\displaystyle D}$ ${\displaystyle d-{i,j}}$ ${\displaystyle i}$ ${\displaystyle j}$

The Floyd algorithm presented also works with negative weights, the Dijkstra algorithm only allows positive edge weights.

Dijkstra's algorithm

→ Main article : Dijkstra's algorithm

The Dijkstra algorithm is actually an algorithm for solving the single source shortest path problem. However, it can be used to solve the all-pair shortest paths problem by running it as the start node for every node in the graph.

In pseudocode, a corresponding implementation can look like this:

 1    func DijkstraSSSP(G,v) {
 2        ... //Standard SSSP-Implementierung hier
 3        return dv;
 4    }
 5
 6    func DijkstraAPSP(G) {
 7        D := |V|x|V|-Matrix
 8        for i from 1 to |V| {
 9           //D[v] bezeichnet die v-te Zeile von D
 10          D[v] := DijkstraSSP(G,i)
 11       }
 12   }

In this example it is assumed that DisjktraSSSP needs the graph and the start node as input . An array of the distances is then returned . The -th element in the array contains the distance from to the node ; This list therefore corresponds exactly to the -th line in the APSP distance matrix . The algorithm for solving the APSP problem accordingly iterates over all nodes of the graph , executes each and saves the result in the corresponding row of the distance matrix. ${\displaystyle G}$ ${\displaystyle v}$ ${\displaystyle d_{v}}$ ${\displaystyle i}$ ${\displaystyle v}$ ${\displaystyle i}$ ${\displaystyle v}$ ${\displaystyle D}$ ${\displaystyle G}$DijkstraSSSP

Since we assume a representation of the graph as an adjacency matrix, DijkstraSSSPa running time of . This results in a sequential runtime of . ${\displaystyle O(|V|^{2})}$DijkstraAPSP ${\displaystyle O(|V|^{3})}$

Parallelization for a maximum of processors ${\displaystyle |V|}$

A simple parallelization results from distributing the loop from DijkstraAPSPin line 8 . However, this is DijkstraSSSPonly possible when using the sequential mode if at most as many processors participate as the loop has iterations. This means that there is an upper limit for the number of processors that can be used for this parallelization. ${\displaystyle |V|}$

Thus z. B. if the number of processors is equal to the number of nodes , that each processor executes the exactly once . If, however, z. If, for example, only processors are available, each processor must call twice . ${\displaystyle p}$ ${\displaystyle |V|}$DijkstraSSSP ${\displaystyle p={\frac {|V|}{2}}}$DijkstraSSSP

Overall, this results in a running time of , if is a multiple of . The efficiency of this parallelization is perfect: By using processors, the runtime is reduced by the factor . ${\displaystyle O(|V|^{2}\cdot {\frac {|V|}{p}})}$ ${\displaystyle |V|}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

This parallelization has another advantage: There is no communication between the processors. An exception is the eventual distribution of the graph before the calculation or the collection of the results afterwards. However, it is assumed that each processor has enough memory to completely store the adjacency matrix of the graph.

Parallelization for more than processors ${\displaystyle |V|}$

If you want to use more than processors for parallelization, several of these must participate in the calculation of at the same time . For this reason, this parallelization takes place over several levels. ${\displaystyle |V|}$DijkstraSSSP

First, the processes are divided into groups. Each group is responsible for computing a row in the distance matrix , i.e. H. for evaluating with a fixed start node. So each group is the size of processors. The results of the groups are independent of each other, so they can work in parallel. The parallelization presented in the previous section therefore corresponds to a group size of 1 for processors. ${\displaystyle |V|}$ ${\displaystyle D}$DijkstraSSSP ${\displaystyle k={\frac {p}{|V|}}}$ ${\displaystyle p=|V|}$

The main difficulty now is that processors have to parallelize the execution of . The idea to solve this problem is to distribute the management of the distance list in DijkstraSSSP within the group. Each processor in the group is therefore exclusively responsible for elements of the list. Be z. B. and . This results in a group size of . Then the first processor of a group stores and manages each time , and the second as well . The entire distance list is included . ${\displaystyle k}$DijkstraSSSP ${\displaystyle d_{v}}$ ${\displaystyle {\frac {|V|}{k}}}$ ${\displaystyle |V|=4}$ ${\displaystyle p=8}$ ${\displaystyle k=2}$ ${\displaystyle d_{v,1}}$ ${\displaystyle d_{v,2}}$ ${\displaystyle d_{v,3}}$ ${\displaystyle d_{v,4}}$ ${\displaystyle d_{v}=[d_{v,1},d_{v,2},d_{v,3},d_{v,4}]}$

DijkstraSSSPessentially consists of repeating two steps: First, the currently next node in the distance list must be found. The shortest route is now known for. Then the distances in for all neighbors of have to be updated. ${\displaystyle x}$ ${\displaystyle d_{v}}$ ${\displaystyle x}$ ${\displaystyle d_{v}}$ ${\displaystyle x}$

The parallelization is now distributed, so the steps must be adapted as follows: ${\displaystyle d_{v}}$

1. Find the node with the currently shortest distance in ${\displaystyle x}$ ${\displaystyle d_{v}}$
   • Each processor has a part of the distance list : Find in it the local minimum , e.g. B. via linear search. ${\displaystyle d_{v}}$ ${\displaystyle {\tilde {x}}}$
   • Find the global minimum in using a reduction operation over all will . ${\displaystyle x}$ ${\displaystyle d_{v}}$ ${\displaystyle {\tilde {x}}}$ ${\displaystyle x}$
   • Again, share the global minimum with all processors in the group via a broadcast operation. ${\displaystyle x}$
2. Update the distances in for all neighbors of ${\displaystyle d_{v}}$ ${\displaystyle x}$
   • Each node now knows the next node and its distance from the start node. This allows him to update the neighbors he manages in . ${\displaystyle x}$ ${\displaystyle d_{v}}$

The total effort of such an iteration of DijkstraSSSPthrough a group of the size is made up as follows: ${\displaystyle k}$

• linear search for : ${\displaystyle {\tilde {x}}}$ ${\displaystyle O({\frac {|V|}{k}})}$
• Broadcast and reduction: These can e.g. B. can be implemented efficiently using binomial trees, which corresponds to a communication effort of approximately . ${\displaystyle O(\log k)}$

For iterations this results in a total running time in . If you now insert the definition of , the result is for a runtime of . ${\displaystyle |V|}$ ${\displaystyle O(|V|({\frac {|V|}{k}}+\log k))}$ ${\displaystyle k}$DijkstraAPSP ${\displaystyle O({\frac {|V|^{3}}{p}}+\log p)}$

One advantage of this parallelization is that not every processor has to save the complete graph. It is sufficient if each processor in each group stores only those columns of the adjacency matrix which belong to the nodes for which the processor is responsible. With a group size of , each processor only needs to store columns of the adjacency matrix. However, this advantage is offset by the disadvantage that the processors have to communicate with one another in order to obtain the overall result. ${\displaystyle k}$ ${\displaystyle {\frac {|V|}{k}}}$

example

The example graph illustrated in the picture with four nodes is given.

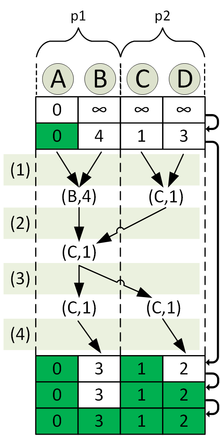
Now the distance matrix is ​​to be calculated using processors. Therefore four groups are formed, each containing two processors. Now consider the group to calculate the shortest paths from node A is in charge of. The processors involved are p1 and p2 . ${\displaystyle p=8}$

The process of calculating the distance list is shown in the following figure. ${\displaystyle d_{A}}$

The top line corresponds to the initialization, the bottom line to the end of the algorithm. Moreover, the distribution is such that p1 for the nodes A and B , and p2 for the nodes C and D is responsible. Accordingly, it is distributed across both processors. For the second iteration of the algorithm, the sub-steps are explicitly shown as an example: ${\displaystyle d_{A}}$ ${\displaystyle d_{A}}$ ${\displaystyle d_{A}}$

1. Calculation of the local nearest node in ${\displaystyle d_{A}}$
2. Calculation of the globally nearest node in using a reduction operation. ${\displaystyle d_{A}}$
3. Announcement of the globally closest node in through a broadcast operation. ${\displaystyle d_{A}}$
4. Marking the globally closest node in as "done" and updating the distances to its neighbors in . ${\displaystyle d_{A}}$ ${\displaystyle d_{A}}$

Floyd algorithm

The Floyd algorithm solves the all-pairs shortest path problem for graphs. It is based on the calculation of a | V | x | V | matrix, in which the entries in the matrix describe the length of the paths between two nodes. Shorter paths are iteratively calculated so that the matrix contains the shortest paths at the end. The following pseudocode describes a sequential variant of the Floyd algorithm:

 1    func Floyd_All_Pairs_SP(A) {
 2         ${\displaystyle D^{(0)}}$ = A;
 3        for k := 1 to n do
 4            for i := 1 to n do
 5                for j := 1 to n do
 6                     ${\displaystyle d_{i,j}^{(k)}:=min(d_{i,j}^{(k-1)},d_{i,k}^{(k-1)}+d_{k,j}^{(k-1)})}$
 7     }

A is the adjacency matrix of the graph, n = | V | the number of nodes and D the distance matrix. For more details on the sequential algorithm, refer to the Floyd and Warshall algorithm .

Parallelization

Allocation of a matrix to processors according to the 2-D block mapping

The basic idea for parallelizing the algorithm is to distribute the calculation of the matrix to the processors. An equally large part of the matrix is ​​assigned to each processor. A common way of doing this is through 2-D block mapping . The matrix is ​​divided into squares and each processor is assigned a square. With a matrix and p processors, each processor calculates a large section of the matrix. Figure 1 shows such a breakdown. With processors, each processor would calculate exactly one entry. As a result, the algorithm only scales up to a maximum number of processors. In the following, we denote the processor that is assigned to the square of the i-th row and j-th column. ${\displaystyle n\times n}$ ${\displaystyle n/{\sqrt {(}}p)\times n/{\sqrt {(}}p)}$ ${\displaystyle p=n^{2}}$ ${\displaystyle n^{2}}$ ${\displaystyle p_{i,j}}$

Since the calculations of the individual parts of the matrix depend on results from other areas, the processors have to communicate with each other and exchange data between the iterations. In the following we describe with the entry of row i and column j of the matrix after the k th iteration. In order to calculate are as indicated in line 6 of the algorithm , and required. every processor has at its disposal because it calculated it itself in the previous iteration. ${\displaystyle d_{i,j}^{(k)}}$ ${\displaystyle d_{i,j}^{(k)}}$ ${\displaystyle d_{i,j}^{(k-1)}}$ ${\displaystyle d_{i,k}^{(k-1)}}$ ${\displaystyle d_{k,j}^{(k-1)}}$ ${\displaystyle d_{i,j}^{(k-1)}}$

In addition, each processor needs a part of the kth row and the kth column from the matrix. is on a processor in the same column and on a processor in the same row as the processor that has to calculate. Each processor that has calculated a part of the k-th row sends this part to all processors in its column. Every processor that has calculated in a part of the k-th column sends this to all processors in the same row. All these processors therefore carry out a one-to-all broadcast operation along the row or column of the processors. This operation is illustrated in Figure 2. ${\displaystyle D^{k-1}}$ ${\displaystyle d_{i,k}^{(k-1)}}$ ${\displaystyle d_{k,j}^{(k-1)}}$ ${\displaystyle d_{i,j}^{(k)}}$ ${\displaystyle D^{k-1}}$ ${\displaystyle D^{k-1}}$

This results in the following algorithm for the variant with 2-D block mapping:

 1    func Floyd_All_Pairs_Parallel( ${\displaystyle D^{(0)}}$) {
 2      for k := 1 to n do{
 3          Jeder Prozessor  ${\displaystyle p_{i,j}}$ der einen Teil der k-ten Reihe von  ${\displaystyle D^{(k-1)}}$ hat,
            broadcastet diesen zu den Prozessoren  ${\displaystyle p_{*,j}}$;
 4          Jeder Prozessor  ${\displaystyle p_{i,j}}$ der einen Teil der k-ten Spalte von  ${\displaystyle D^{(k-1)}}$ hat,
            broadcastet diesen zu den Prozessoren  ${\displaystyle p_{i,*}}$;
 5          Jeder Prozessor wartet bis die benötigten Daten vorhanden sind;
 6          Jeder Prozessor berechnet seinen Teil der  ${\displaystyle D^{(k)}}$ matrix;
 7          }
 8     }

Data dependencies in the parallel Floyd algorithm

In line 5 of the algorithm we have a synchronization step. This ensures that all data required for the next iteration are available on every processor. In order to improve the runtime, this synchronization step can be removed without affecting the correctness of the algorithm. In order to achieve this, each processor immediately starts the calculation as soon as it has the parts relevant to its part of the matrix. This variant of parallelization is known as pipelined 2-D block mapping .

running time

The runtime of the sequential algorithm is dominated by the three nested for loops. The calculation in line 6 can be carried out in constant time ( ). This results in a running time of for the sequential algorithm. ${\displaystyle O(1)}$ ${\displaystyle O(n^{3})}$

2-D block mapping

The running time of the parallelized algorithm consists of two parts. The time for the calculations and the time for data exchange and communication between the processors.

Since the method does not involve any additional calculations and the calculations are divided equally between the p processors, we have a runtime of for this part . ${\displaystyle O(n^{3}/p)}$

In each iteration of the algorithm, a one-to-all broadcast operation is carried out with elements along the row or column of the processors. A synchronization step is then carried out. How much time these operations require depends on the architecture of the parallel computer used. This means that additional time is required for data exchange and communication . ${\displaystyle n/{\sqrt {p}}}$ ${\displaystyle T_{Kommunikation}=n(T_{synch}+T_{broadcast})}$

Overall, this results in a running time of:

${\displaystyle T_{Gesamt}=O(n^{3}/p)+n(T_{synch}+T_{broadcast})}$

Pipelined 2-D block mapping

For the runtime of the data exchange between the processors in the pipelined version of the algorithm, we assume that a processor can transfer k data objects to an adjacent processor in O (k) time. In each step, elements of a row are sent to the neighboring processors. Similarly, elements of a column are sent to the neighboring processors. Such a step takes O ( ) time. After taking steps, the relevant data of the first row and column have then arrived at the processor . So after O (n) time. ${\displaystyle n/{\sqrt {p}}}$ ${\displaystyle n/{\sqrt {p}}}$ ${\displaystyle n/{\sqrt {p}}}$ ${\displaystyle {\sqrt {p}}}$ ${\displaystyle p_{{\sqrt {p}},{\sqrt {p}}}}$

The data of the other rows and columns then come successively after O ( ) time and can be processed like a pipeline. ends its last iteration after O ( ) + O ( ) time. The additional time required for the data exchange is therefore O ( ). ${\displaystyle n^{2}/p}$ ${\displaystyle p_{{\sqrt {p}},{\sqrt {p}}}}$ ${\displaystyle n^{3}/p}$ ${\displaystyle n}$ ${\displaystyle n}$

This results in the following total runtime for pipelined 2-d block mapping:

${\displaystyle T_{Gesamt}=O(n^{3}/p)+O(n)}$

literature

• A. Grama: Introduction to parallel computing. Pearson Education, 2003.
• V. Kumar: Scalability of Parallel Algorithms for the All-Pairs Shortest-Path Problem. Journal of Parallel and Distributed Programming 13, 1991.
• I. Foster: Designing and Building Parallel Programs (Online).
• Bindell, Fall: Parallel All-Pairs Shortest Paths Applications of Parallel Computers, 2011.