Floyd and Warshall's algorithm

The Floyd and Warshall algorithm (also Floyd-Warshall algorithm or triple algorithm ), named after Robert Floyd and Stephen Warshall , is an algorithm of graph theory . In Floyd's version, it finds the shortest paths between all pairs of nodes in a graph and calculates their length ( APSP, all-pairs shortest path ). In Warshall's version he finds the transitive envelope of a graph. Both versions were introduced in 1962 and go back to an algorithm that Stephen Kleene published in 1956 in connection with regular expressions .

description

The Floyd Warshall algorithm is based on the principle of dynamic programming .

The Floyd algorithm is based on the following observation:

If the shortest path goes from to through , then the partial paths from to and from to are already minimal. So it is assumed you already know the shortest paths between all pairs of nodes, the only nodes as small with index lead, and you look all shortest paths across nodes with index at most , you have a path from to two possibilities: either he goes over the node , then it is composed of already known paths from to and from to , or it is the already known path from to via node with an index smaller than . ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle w}$ ${\displaystyle u}$ ${\displaystyle w}$ ${\displaystyle w}$ ${\displaystyle v}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle k}$ ${\displaystyle u}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle v}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle k}$

Suppose the graph is given by its weight matrix . ${\displaystyle w}$

${\displaystyle w\left[i,j\right]}$is the weight of the edge from to , if such an edge exists. If there is no edge from to , it is infinite. ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle w\left[i,j\right]}$

Then the matrix of shortest distances can be determined by the following procedure: ${\displaystyle d}$

Algorithmus von Floyd

(1) Für alle  ${\displaystyle i,j:d\left[i,j\right]=w\left[i,j\right]}$
(2) Für  ${\displaystyle k=1}$ bis  ${\displaystyle n}$
(3)   Für alle Paare  ${\displaystyle i,j}$
(4)      ${\displaystyle d\left[i,j\right]=\min(d\left[i,j\right],d\left[i,k\right]+d\left[k,j\right])}$

If you want to calculate the transitive hull , you change the algorithm as follows:

${\displaystyle w}$is the adjacency matrix , that is, is 1 if there is an edge from to , and 0 if there is no edge. ${\displaystyle w\left[i,j\right]}$ ${\displaystyle i}$ ${\displaystyle j}$

The matrix is defined in such a way that , if and only if a path from to exists: ${\displaystyle d}$ ${\displaystyle d[i,j]=1}$ ${\displaystyle i}$ ${\displaystyle j}$

Algorithmus von Warshall

(1) Für  ${\displaystyle k=1}$ bis  ${\displaystyle n}$
(2)   Für  ${\displaystyle i=1}$ bis  ${\displaystyle n}$
(3)     Falls  ${\displaystyle d\left[i,k\right]=1}$
(4)       Für  ${\displaystyle j=1}$ bis  ${\displaystyle n}$
(5)         Falls  ${\displaystyle d\left[k,j\right]=1}$
(6)            ${\displaystyle d\left[i,j\right]=1}$

Line (6) is set to 1 if and only if a path from to and a path from to over edges with an index smaller than exist. ${\displaystyle d\left[i,j\right]}$ ${\displaystyle i}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle j}$ ${\displaystyle k}$

The Floyd algorithm also works when the edges have negative weight. Cycles with a negative length (unlike the Bellman-Ford algorithm ) are not recognized and lead to an incorrect result. However, negative cycles can be recognized in retrospect by negative values ​​on the main diagonal of the distance matrix . In order to avoid numerical problems, this should not be tested afterwards, but every time a diagonal element is changed in line (4).

Time complexity

The running time ( complexity ) of the Floyd-Wars Hall algorithm is because for the three variables , , the values from 1 to have to be passed. Where is the number of nodes in the graph . ${\displaystyle {\mathcal {O}}(n^{3})}$ ${\displaystyle k}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle n}$ ${\displaystyle n}$

example

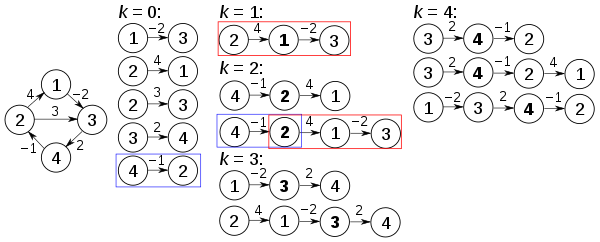
The algorithm is carried out on the graph at the bottom left with four nodes :

Before the first iteration of the outer loop, labeled k = 0 above, the only known paths correspond to the individual edges in the diagram . If k = 1, paths are found that run through node 1: In particular, path [2,1,3] is found, which replaces path [2,3], which has fewer edges but is longer. With k = 0, d [2, 3] = 3 and with k = 1 this value becomes with d [2, 3] = d [2, 1] + d [1, 3] = 4 + (-2) = 2 overwritten. If k = 2, paths are found which run through the nodes {1,2}. The red and blue boxes show how path [4,2,1,3] is put together from the two known paths [4,2] and [2,1,3] that were encountered with intersection 2 in previous iterations . Path [4,2,3] is not taken into account because [2,1,3] is the shortest path that has been encountered from 2 to 3 so far. If k = 3, all paths are found that run through the nodes {1,2,3}. Finally, if k = 4, all shortest paths are found.

The distance matrix at each iteration of k with the updated distances in bold is:

k = 0		j
		1	2	3	4th
i	1	0	∞	−2	∞
	2	4th	0	3	∞
	3	∞	∞	0	2
	4th	∞	−1	∞	0

k = 1		j
		1	2	3	4th
i	1	0	∞	−2	∞
	2	4th	0	2	∞
	3	∞	∞	0	2
	4th	∞	−1	∞	0

k = 2		j
		1	2	3	4th
i	1	0	∞	−2	∞
	2	4th	0	2	∞
	3	∞	∞	0	2
	4th	3	−1	1	0

k = 3		j
		1	2	3	4th
i	1	0	∞	−2	0
	2	4th	0	2	4th
	3	∞	∞	0	2
	4th	3	−1	1	0

k = 4		j
		1	2	3	4th
i	1	0	−1	−2	0
	2	4th	0	2	4th
	3	5	1	0	2
	4th	3	−1	1	0

Other methods for calculating shortest paths

• Min-plus matrix multiplication algorithm
• A * algorithm
• Dijkstra's algorithm
• Bellman-Ford algorithm

literature

• Robert W. Floyd : Algorithm 97 (SHORTEST PATH) . In: Communications of the ACM 5, 1962, 6, p. 345.
• Stephen Warshall: A Theorem on Boolean Matrices . In: Journal of the ACM 9, 1962, 1, ISSN  0004-5411 , pp. 11-12.

Web links

• Explanation of the algorithm with example and references
• Interactive HTML5 demonstration from the Technical University of Munich
• Java applet for demonstration
• Robert W. Floyd: Algorithm 97 (SHORTEST PATH), in Communications of the ACM, 5 (6), p. 345, 1962.

Individual evidence

1. ↑ Stefan Hougardy: The Floyd – Warshall algorithm on graphs with negative cycles . In: Information Processing Letters . 110, No. 8-9, April 2010, pp. 279-281.