SEPIC

A SEPIC (short for English single-ended primary inductance converter ) is in the electronics a form of DC-DC converter . The positive input voltage U _E of the SEPIC can also be less than the positive output voltage U both greater than _A to be. The circuit was presented in 1977 by Massey and Snyder at the PESC (Power Electronic Specialist Conference).

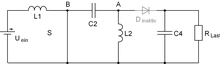
Circuit diagram of a SEPIC converter

circuit

Three energy stores and a switch (S) act as an essential element of the circuit. The energy stores are two coils (L1 and L2) and a capacitor (C2). These can be designed as a double coil with two oppositely wound turns on the same core or two independent coils. In the second case, the coil L2 can also be designed as a transformer. This enables galvanic separation.

The Ćuk converter and the Zeta converter have a topology similar to that of the SEPIC.

One advantage of capacitor-coupled switching regulators is that no short-circuit current can flow from the input to the output and back. However, since the coupling capacitor converts a power loss, the efficiency is lower than that of other topologies.

Continuous operation

When examining the SEPIC, a basic distinction must be made between two operating modes. The SEPIC can work in continuous and discontinuous operation. At the beginning the continuous operation ( Continuous Current Mode ) should be described. The designation refers to the current in coil L1. Continuous operation can be divided into two time periods. The first section corresponds to the time in which the switch S is closed.

Equivalent circuit for the first time period (S closed, D blocked)

The second section represents the remaining time that the switch is open.

Equivalent circuit diagram for the second time segment (S open, D conducts)

The investigation is carried out by considering the currents within the circuit. The assumption is that capacitor C2 is large enough that the voltage across the capacitor does not change. It can also be determined that the capacitor charges exactly to the value of the input voltage. When the switch is closed, the following increases in current occur for L1 and L2:

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}={\frac {U_{\mathrm {ein} }}{L}}}$ (1).

If you take both coils into account, the result is

${\displaystyle I={\frac {U_{\mathrm {ein} }}{L_{1}}}t+{\frac {U_{\mathrm {ein} }}{L_{2}}}t+I_{0}}$

${\displaystyle =U_{\mathrm {ein} }\left({\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}\right)t+I_{0}}$ (2).

The peak value of the current at the end of section 1 is then calculated as follows

Current curves in CCM operation

${\displaystyle I=U_{\mathrm {ein} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)DT+I_{0}}$ (3)

where D represents the duty cycle . Section 2 begins with this peak value. The current then falls depending on the output voltage.

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=-{\frac {U_{\mathrm {aus} }}{L}}}$ (4)

The following applies to the peak value:

${\displaystyle I=U_{\mathrm {aus} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)(1-D)T+I_{0}}$ (5).

Since the values ​​must be the same at the boundary between section 1 and 2, equations (3) and (5) can be equated.

${\displaystyle U_{\mathrm {ein} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)DT+I_{0}=U_{\mathrm {aus} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)(1-D)T+I_{0}}$ (6).

Solved according to the ratio of the output to the input voltage results

${\displaystyle {\frac {U_{\mathrm {aus} }}{U_{\mathrm {ein} }}}={\frac {D}{1-D}}}$ (7)

Discontinuous operation

The discontinuous operation ( Discontinuous Current Mode ) starts the continuous operation with the two sections. The same equivalent circuit diagrams apply as for continuous operation. This is joined by a third section, during which the two inductances do not carry any current, but the load draws energy from the output capacitor C4, as shown in the equivalent circuit diagram.

Equivalent circuit for the third period

Since the currents of the inductances start at zero and end at zero, I _{0 is} not considered . The equation (3) changes to:

${\displaystyle I=U_{\mathrm {ein} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)\,D\,T}$ (8th)

and equation (5) becomes:

${\displaystyle I=U_{\mathrm {aus} }\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)\,(D_{2})\,T}$ (9)

D ₂ corresponds to the duration of the second time segment. Equated results

${\displaystyle {\frac {U_{\mathrm {aus} }}{U_{\mathrm {ein} }}}={\frac {D}{D_{2}}}}$ (10)

Now the third section is still missing.

The output voltage results from the current and the load resistance.

${\displaystyle U_{\mathrm {aus} }=I_{\mathrm {aus} }\,R_{\mathrm {Last} }}$ (11).

The current corresponds to the average current through the diode D, which still has to be calculated. Only in section 2 is current transferred from the input via the diode into the output capacitor. The mean value of the current based on the entire switching cycle results

${\displaystyle {\begin{aligned}{\bar {I}}_{D}&={\frac {U_{\mathrm {aus} }}{R_{\mathrm {Last} }}}\\&={\frac {1}{2}}U_{\mathrm {ein} }D\;T\;\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)\,D_{2}\end{aligned}}}$ (12).

With equation (10) and equation (12), two equations are available, both of U _A , U _out , D , and D ₂ depend. If you convert both equations according to D ₂ and equate them, you can determine the ratio of the output to the input voltage:

${\displaystyle \left({\frac {U_{\mathrm {aus} }}{U_{\mathrm {ein} }}}\right)^{2}={\frac {1}{2}}\,D^{2}\,T\,R_{\mathrm {Last} }\,\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)}$ (13)

and thus

${\displaystyle {\frac {U_{\mathrm {aus} }}{U_{\mathrm {ein} }}}=D\,{\sqrt {{\frac {1}{2}}\,T\,R_{\mathrm {Last} }\,\left({\frac {L_{1}+L_{2}}{L_{1}\cdot L_{2}}}\right)}}}$ (14)

In the discontinuous operation of the SEPIC, the output voltage is not only dependent on the switch-on time of the switch.

Web links

• Interactive power electronics seminar (Java animations)
• National Semiconductor (now Texas Instruments) design guidelines in Application Note 1484

Individual evidence

1. ^ RP Massey, EC Snyder: High Voltage Single-Ended DC-DC Converter . In: Proc. IEEE PESC '77 Record . 1977, p. 156-159 .