Turan's theorem

The set of Turán (after Pál Turán ) is a statement of the mathematical part area of the graph theory . It makes a statement about the maximum number of edges that a graph with a given number of nodes can have without having to contain a complete subgraph with nodes. ${\displaystyle m}$

The case of the triangles

Let it be an undirected graph with nodes. A subgraph made up of three nodes is obviously called a triangle if two of these three nodes are connected by an edge. Turán's theorem specifies the statement that if the graph is not to contain any triangles, it cannot have too many edges: ${\displaystyle G}$ ${\displaystyle n}$

• Turán's theorem (triangles) : If a graph with nodes has no triangles, it has at most edges. ${\displaystyle G}$ ${\displaystyle n}$ ${\displaystyle \left\lfloor {\frac {n^{2}}{4}}\right\rfloor }$

Where is the largest whole number that is less than or equal to . ${\displaystyle \lfloor x\rfloor }$ ${\displaystyle x}$

For small , the statement is clear: ${\displaystyle n}$

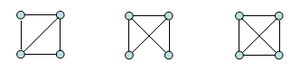
Graphs with 4 nodes and at least 5 edges contain at least one triangle.

• ${\displaystyle n=1}$: This graph has neither edges nor triangles and it is . ${\displaystyle \left\lfloor {\frac {1^{2}}{4}}\right\rfloor =0}$
• ${\displaystyle n=2}$: Such graphs have no triangles and at most one edge; it is . ${\displaystyle \left\lfloor {\frac {2^{2}}{4}}\right\rfloor =1}$
• ${\displaystyle n=3}$: Such graphs have a triangle if and only if the number of edges is 3; and it is . ${\displaystyle \left\lfloor {\frac {3^{2}}{4}}\right\rfloor =2}$
• ${\displaystyle n=4}$: It is and actually every 4-way graph with 5 edges has at least one triangle. ${\displaystyle \left\lfloor {\frac {4^{2}}{4}}\right\rfloor =4}$

For larger ones, the statement is reduced to graphs with nodes, which then enables an induction proof, whereby one has to distinguish between even and odd . The case is only briefly indicated here: ${\displaystyle n}$ ${\displaystyle n-2}$ ${\displaystyle n}$ ${\displaystyle n}$

If you remove a and b from G, only the black edges remain.

Take away an edge that two nodes , and connects, from . The subgraph obtained in this way also contains no triangles and only nodes, i.e. according to the induction assumption at most edges. The graph also has the distant edge and further edges that start or end and end in. Go about by , so must of outgoing edges on other nodes from forming, because otherwise contained a triangle, that is, can at most edges out ending. The maximum possible number of edges is therefore . The assertion for straight follows from this . The odd case can be treated quite similarly. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G}$ ${\displaystyle n-2}$ ${\displaystyle \left\lfloor {\frac {(n-2)^{2}}{4}}\right\rfloor ={\frac {(n-2)^{2}}{4}}}$ ${\displaystyle G}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G\setminus \{a,b\}}$ ${\displaystyle k}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G\setminus \{a,b\}}$ ${\displaystyle G}$ ${\displaystyle b}$ ${\displaystyle n-2-k}$ ${\displaystyle G\setminus \{a,b\}}$ ${\displaystyle G}$ ${\displaystyle {\frac {(n-2)^{2}}{4}}+1+k+(n-2-k)\,=\,{\frac {n^{2}-4n+4}{4}}+1+n-2\,=\,{\frac {n^{2}}{4}}-n+1+1+n-2\,=\,{\frac {n^{2}}{4}}}$ ${\displaystyle n}$ ${\displaystyle n}$

The limit given by Turán's Theorem is sharp, as the example of the bipartite graph shows, because this graph has nodes and edges. ${\displaystyle K_{n,n}}$ ${\displaystyle 2n}$ ${\displaystyle n^{2}={\frac {(2n)^{2}}{4}}}$

The Turán graph

A triangle is the complete graph . The question arises whether one can specify an upper limit for the number of edges in a graph that does not contain a subgraph that is too isomorphic. In order to answer this question, the so-called Turán graph is defined as follows: ${\displaystyle K_{3}}$ ${\displaystyle K_{m}}$

The Turán graph ${\displaystyle T_{3}(7)}$

The Turán graph is the complete m-partite graph which has elements in the kth class . Note that ${\displaystyle T_{m}(n)}$ ${\displaystyle \left\lfloor {\frac {n+k-1}{m}}\right\rfloor }$

${\displaystyle \left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\ldots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor =n}$

holds and therefore has nodes. The number of edges of going with designated. You can show that ${\displaystyle T_{m}(n)}$ ${\displaystyle n}$ ${\displaystyle T_{m}(n)}$ ${\displaystyle t_{m}(n)}$

${\displaystyle t_{m}(n)={\frac {(m-1)(n^{2}-r^{2})}{2m}}+{\frac {r(r-1)}{2}}}$

where is and stands for division by remainder . ${\displaystyle r\equiv n\,\mathrm {mod} \,m,\,\,0\leq r<m}$ ${\displaystyle \mathrm {mod} }$

The Turán graph opposite therefore has edges. ${\displaystyle T_{3}(7)}$ ${\displaystyle {\frac {(3-1)(49-1)}{2\cdot 3}}+{\frac {1\cdot (1-1)}{2}}={\frac {2\cdot 48}{6}}=16}$

A slight calculation shows . This upper estimate of the number of edges of the Turán graph is often used. ${\displaystyle t_{m}(n)={\frac {n^{2}}{2}}\left(1-{\frac {1}{m}}+{\frac {r^{2}}{mn^{2}}}-{\frac {r}{n^{2}}}\right)\leq {\frac {n^{2}}{2}}\left(1-{\frac {1}{m}}\right)}$

The general case

• Turán's theorem : If a graph with nodes has no subgraph ( ) that is too isomorphic , it has at most edges. Any graph without an isomorphic subgraph with nodes and edges is isomorphic to the Turán graph . ${\displaystyle G}$ ${\displaystyle n}$ ${\displaystyle K_{m}}$ ${\displaystyle m\geq 3}$ ${\displaystyle t_{m-1}(n)}$ ${\displaystyle K_{m}}$ ${\displaystyle n}$ ${\displaystyle t_{m-1}(n)}$ ${\displaystyle T_{m-1}(n)}$

In extremal graph theory , the number of a graph is defined as the maximum number of edges that a graph with nodes and without a subgraph that is too isomorphic can have. Turan's theorem therefore has the following corollary: ${\displaystyle H}$ ${\displaystyle \mathrm {ex} (n,H)}$ ${\displaystyle n}$ ${\displaystyle H}$

${\displaystyle \mathrm {ex} (n,K_{m})\,=\,t_{m-1}(n)\leq {\frac {n^{2}}{2}}\cdot (1-{\frac {1}{m-1}})}$

Turán's theorem says more, namely that every two graphs with nodes without a subgraph that is too isomorphic that realize this extreme value are to be isomorphic . ${\displaystyle n}$ ${\displaystyle K_{m}}$ ${\displaystyle T_{m-1}(n)}$

Is and straight, so is and therefore . Is odd, so is and therefore . Therefore, and one obtains the special case of triangles already discussed above. ${\displaystyle m=3}$ ${\displaystyle n}$ ${\displaystyle 0\equiv n\,\mathrm {mod} \,2}$ ${\displaystyle t_{2}(n)={\frac {(2-1)(n^{2}-0^{2})}{2\cdot 2}}+0={\frac {n^{2}}{4}}}$ ${\displaystyle n}$ ${\displaystyle 1\equiv n\,\mathrm {mod} \,2}$ ${\displaystyle t_{2}(n)={\frac {(2-1)(n^{2}-1^{2})}{2\cdot 2}}+0={\frac {n^{2}-1}{4}}=\lfloor {\frac {n^{2}}{4}}\rfloor }$ ${\displaystyle \mathrm {ex} (n,K_{3})\,=\,\lfloor {\frac {n^{2}}{4}}\rfloor }$

The restriction made in the sentence can be weakened too much, even if the resulting case is not particularly interesting. A graph without a subgraph that is too isomorphic is an edgeless graph and indeed is for everyone . The cases do not have to be ruled out either. For is in the formula given above for , and it is therefore ; one obtains the trivial statement that a graph with nodes contains a subgraph that is too isomorphic if and only if it is complete, because it has edges. Is , so is and therefore , is so is and therefore also ; that is, in those cases the graph can have as many edges as possible, which is clear since it cannot contain any too isomorphic subgraphs anyway . ${\displaystyle m\geq 3}$ ${\displaystyle m\geq 2}$ ${\displaystyle K_{2}}$ ${\displaystyle t_{1}(n)=0}$ ${\displaystyle n}$ ${\displaystyle m\geq n}$ ${\displaystyle m=n}$ ${\displaystyle r=1}$ ${\displaystyle t_{m}(n)}$ ${\displaystyle t_{n-1}(n)={\frac {(n-2)(n^{2}-1)}{2(n-1)}}+0={\frac {(n-2)(n+1)}{2}}={\frac {n(n-1)}{2}}-1}$ ${\displaystyle n}$ ${\displaystyle K_{n}}$ ${\displaystyle K_{n}}$ ${\displaystyle {\frac {n(n-1)}{2}}}$ ${\displaystyle m=n+1}$ ${\displaystyle r=0}$ ${\displaystyle t_{m}(n)={\frac {n(n-1)}{2}}}$ ${\displaystyle m>n+1}$ ${\displaystyle r=n}$ ${\displaystyle t_{m-1}(n)={\frac {r(r-1)}{2}}={\frac {n(n-1)}{2}}}$ ${\displaystyle m>n}$ ${\displaystyle K_{m}}$

literature

• K. Wagner: Graph theory . Bibliographisches Institut, Mannheim 1970, ISBN 3-411-00248-4
• P. Turan: An extreme problem from graph theory . In: Mat. Fiz. Lapok. , 48, 1941, pp. 436–452 (Hungarian)

Individual evidence

1. ^ Frank Harary : Graph theory. R. Oldenbourg, Munich 1974, ISBN 3-486-34191-X .
2. ^ Béla Bollobás : Graph Theory, An Introductory Course . Springer Verlag, New York 1979, ISBN 0-387-90399-2 , IV, §2, Theorem 6