Stochastic tunneling

Stochastic tunneling (STUN) is a method for global optimization in which the function to be minimized is sampled using the Monte Carlo method .

principle

Schematic one-dimensional test function (black) and effective STUN potential (red and blue), where the minimum marked with arrows represents the best minimum found so far. All potential pots that are above the best minimum found are suppressed. If the dynamic process can escape the potential well around the current minimum, it will not be absorbed by other, higher local minima. Potential wells with lower minima are reinforced, which speeds up the dynamic process.

Optimization algorithms based on the Monte Carlo method scan the examined function by jumping randomly from the current solution to another solution, with the function values ​​differing by . The defined Metropolis criterion is usually chosen as the probability of such a test jump, with the parameter being chosen appropriately. ${\displaystyle \Delta E}$ ${\displaystyle \min \left(1;\exp \left(-\beta \cdot \Delta E\right)\right)}$ ${\displaystyle \beta }$

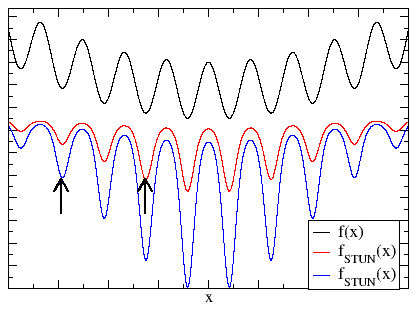
The principle of STUN is to circumvent the slow dynamics of unfavorably shaped energy functions, which are found in spin glasses , for example , by tunneling through such barriers. This goal is achieved by Monte Carlo sampling of the transformed function, which is not subject to this slow dynamic. The transformation is defined in the "standard form" by , being the lowest function value found so far. This transformation preserves the geometric locations of the minima. The effect of such a transformation is shown in the figure. ${\displaystyle f_{STUN}:=1-\exp \left(-\gamma \cdot \left(f(x)-f_{o}\right)\right)}$ ${\displaystyle f_{o}}$

An adaptive variant of the method makes it possible to estimate the parameters of the method itself "online" and thereby improve the efficiency of the algorithm.

Other approaches

• Simulated cooling
• Parallel tempering
• Evolutionary Algorithm
• Differential evolution

Individual evidence

1. ↑ K. Hamacher and W. Wenzel: The Scaling Behavior of Stochastic Minimization Algorithms in a Perfect Funnel Landscape . Phys. Rev. E 59 (1): 938-941, 1999
2. ^ W. Wenzel and K. Hamacher: A Stochastic tunneling approach for global minimization . Phys. Rev. Lett. 82 (15): 3003-3007, 1999
3. ↑ Metropolis, M.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E .: Equation of state calculations by fast computing machines . J. Chem. Phys 21 (1953), pp. 1087-1092
4. ↑ K. Hamacher: Adaptation in Stochastic Tunneling Global Optimization of Complex Potential Energy Landscapes . Europhys. Lett. 74 (6): 944, 2006