Talbot effect

Monochromatic Talbot effect: the slits of a comb in the light beam (period 1 mm) are repeated 1.5 m away from the comb. (Due to the camera perspective, the stripes are partly oblique)

The Talbot effect is visible in near-field diffraction on a (diffraction) grating : The brightness distribution at certain Talbot distances behind a grating corresponds exactly to the structure of the grating itself. The effect was created in 1836 by William Henry Fox Talbot with a fine beam of sunlight discovered.

description

Basic structure (light source is at the bottom right)

Illustration of the Talbot effect. The grid of period d is drawn in black. The black points mean intensity maxima.

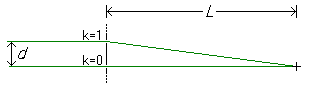
In the most basic case (see illustration), a grating is irradiated by plane monochromatic waves (for example, an expanded laser beam):

• If you place an observation screen at a distance L _Talbot (or an integral multiple thereof) behind the grid, an image of the grid is obtained.
• At the distance L _Talbot / 2 = d ² / λ (or an odd multiple thereof) one obtains an image shifted by d / 2 (indicated in the figure by black dots for the intensity maxima).
• Between two self-images there are further images of the grid with increased period (provided the grid has sufficiently narrow gaps). If the position of the observation screen is continuously changed in the case of very narrow gaps and applied along the side of the image generated, a Talbot carpet is created that shows the structure of the self-images.
• If the direction of the incident light changes, the image shifts in the opposite direction, as if it were a shadow cast by the grid.

The following applies to the Talbot distance L _Talbot with illumination with the wavelength : ${\displaystyle \lambda \ll d}$

${\displaystyle L_{\mathrm {Talbot} }={\frac {2d^{2}}{\lambda }}}$

The effect can be used for wavelengths of completely different orders of magnitude, because a change in λ by the factor x can only be compensated for by changing the grating period (with the Talbot distance unchanged). ${\displaystyle d}$ ${\displaystyle {\sqrt {x}}}$

The simple expression is an approximation if the feature size (grating period) is much larger than the wavelength. The general expression is: ${\displaystyle {\frac {2d^{2}}{\lambda }}}$

${\displaystyle L_{\mathrm {Talbot} }={\frac {\lambda }{1-{\sqrt {1-\lambda ^{2}/d^{2}}}}}}$

Demarcation

If the Talbot distance is significantly below or exceeded, other effects dominate. At shorter distances, such as objects from everyday life (e.g. combs), we often observe from distances that are too short, where the casting of shadows dominates. At longer distances, however, Fraunhofer diffraction occurs , in which the light shines as a single beam in certain directions. In the everyday world this corresponds to viewing a CD.

Applications

The Talbot effect is used in research:

• Wavefront measurement: Because the image shifts when the direction of the incident light changes, wavefronts or directions of propagation of light rays can be measured, comparable to a Hartmann-Shack sensor . This means that even small refractive indices can be precisely determined. In the visible range, for example, minimal light refraction caused by hot air (candle) can be detected.
• X-ray: X-ray images usually show a shadow cast ("absorption"), e.g. B. of bones. However, X-rays are also deflected by different indices of refraction . By measuring the deflection, images can be generated that e.g. B. show tissue in more detail.
• Matter waves: According to the De Broglie wavelength , matter can be assigned a wavelength. The Talbot effect has been demonstrated for rays made of atoms or even massive organic molecules:
• For further applications and literature see z. B.

variants

• Two-dimensional grids: The effect occurs along both grid dimensions. Is the grid z. B. from a checkerboard pattern, this is created again in the Talbot distance.
• Spherical waves : If you do not use a laser beam, the differences in distance between interfering light beams add up before and after the grating, which increases the phase differences. If the grid is exactly between the light source and the observation screen, the doubled phase differences must be compensated for by larger distances, the Talbot distance doubles.

Flat polychromatic light source: The colors are created by the dependence of the wavelength. A black grid is printed in the upper part so that a beating is created.

• Flat light source: Incandescent lamps or the focal point in X-ray tubes have a certain size. This size leads to an overlay of stripe patterns, no stripe pattern can be recognized any more (more precisely: the size of the light source reduces the (spatial) coherence of the light source too much). If an additional grid is placed near the light source (with the role of 'coherence grid') so that the individual images of the individual grid columns constructively overlap, the Talbot effect occurs again.
• Polychromatic light source: In the case of multicolored light, the Talbot distance is only correct for a certain wavelength. The wider the grid columns, the better the tolerance for deviations from the design spacing. Talbot himself discovered the effect using a narrow beam of sunlight.

Polychromatic with phase grating in which light rays are delayed by half a wavelength. (The picture lacks blue because the grid (a plastic film) floats in yellowish oil)

• Phase grating : In contrast to (amplitude) gratings (bars opaque), the entire grating can be transparent, the bars delay the light by half a wavelength. Here the grid spacing is greatly reduced to . Furthermore, the effect only occurs with odd multiples of this distance. Especially for the 0-fold distance, the brightness is evenly distributed in the phase grating itself. Phase gratings are often used in the X-ray field. ${\displaystyle L_{\mathrm {Talbot} }/16=d^{2}/(8\lambda )}$
  

Derivation

Geometric derivation : There is constructive interference at point L _Talbot / 4. Here d / λ is interpreted as the slope and the number of slope triangles.

Narrow gaps

The case of the monochromatic plane light wave (wavelength ) is considered. The grid is period , the distance to the screen is . ${\displaystyle \lambda }$ ${\displaystyle d}$ ${\displaystyle L}$

Preliminary consideration Taylor expansion 1st order:

${\displaystyle f(x)=f(x_{0}+\Delta x)=f(x_{0})+\Delta x\cdot f^{\prime }(x_{0})}$, applied to the root gives:

${\displaystyle f(x)={\sqrt {x}}={\sqrt {x_{0}+\Delta x}}={\sqrt {x_{0}}}+\Delta x/(2{\sqrt {x_{0}}})}$.

We compare a direct ray of light (which is perpendicular to the grating ) of length with one that passes through the grating one column further up or down (length , ). Constructive interference occurs when the difference in length z. B. is: ${\displaystyle k=0}$ ${\displaystyle L}$ ${\displaystyle {\sqrt {L^{2}+d^{2}}}}$ ${\displaystyle k=1}$ ${\displaystyle \lambda }$

${\displaystyle \Delta L={\sqrt {L^{2}+d^{2}}}-L={\sqrt {L^{2}}}+{\frac {d^{2}}{2{\sqrt {L^{2}}}}}-L={\frac {d^{2}}{2L}}:=\lambda }$

Result:

• This constructive interference occurs at . (The geometric derivation in the drawing shows this situation.) ${\displaystyle L=d^{2}/(2\lambda )=L_{\mathrm {Talbot} }/4}$
• The extension of the route is the square of the grid column : . This means that light from all of the grid columns interferes constructively at the same point. ${\displaystyle k=0,1,2,\ldots }$ ${\displaystyle {\sqrt {L^{2}+(k\cdot d)^{2}}}-L=k^{2}d^{2}/(2L)=k^{2}\lambda }$

At other distances the conditions are slightly different. This can be shown using the example . The image on the screen is offset by, the ray through one of the two directly adjacent columns has the length , the rays of the next-most distant columns have the lengths . ${\displaystyle L}$ ${\displaystyle L=L_{\mathrm {Talbot} }/2=d^{2}/\lambda }$ ${\displaystyle d/2}$ ${\displaystyle \pm 0{,}5}$ ${\displaystyle {\sqrt {L^{2}+(0{,}5d)^{2}}}}$ ${\displaystyle \pm 1{,}5}$ ${\displaystyle {\sqrt {L^{2}+(1{,}5d)^{2}}}}$

The path length difference between the columns and is then ${\displaystyle n+1{,}5}$ ${\displaystyle n+0{,}5}$

${\displaystyle \Delta L={\sqrt {L^{2}+(n+1{,}5)^{2}d^{2}}}-{\sqrt {L^{2}+(n+0{,}5)^{2}d^{2}}}}$

${\displaystyle {\Delta L={\frac {(n+1{,}5)^{2}d^{2}-(n+0{,}5)^{2}d^{2}}{2L}}={\frac {(n^{2}+3n+2{,}25-n^{2}-n-0{,}25)d^{2}}{2L}}={\frac {(2n+2)d^{2}}{2L}}=(n+1)\lambda }}$

The differences in the path lengths are thus again multiples of and constructive interference occurs. ${\displaystyle \lambda }$

The following important information is missing from this article or section:

Wide gaps (gap share e.g. 50%)

Help Wikipedia by researching and pasting it .

literature

• Changhe Zhou, Wei Wang, Enwen Dai, Liren Liu: Simple Principles of the Talbot Effect . In: Optics and Photonics News . tape 15 , no. 11 , November 1, 2004, pp. 46-50 , doi : 10.1364 / OPN.15.11.000046 .

Individual evidence

1. ^ Henry Fox Talbot: LXXVI. Facts relating to optical science. No. IV . In: The London and Edinburgh Philosophical Magazine and Journal of Science . tape 9 , no. 56 , 1836, §2 Experiments on Diffraction , p. 401–407 ( limited preview in Google Book search).
2. ^ RF Edgar: The Fresnel Diffraction Images of Periodic Structures . In: Optica Acta: International Journal of Optics . tape 16 , no. 3 , 1969, p. 281-287 , doi : 10.1080 / 713818186 .
3. ↑ ESRF X-Ray Phase Contrast , ESRF (European Synchrotron Radiation Source) 2002
4. ↑ ESRF X-Ray Phase Contrast: Petrified Insects , ESRF 2006
5. ↑ ESRF X-Ray Phase Contrast: Brain Sections , ESRF 2008
6. ^ Franz Pfeiffer, Timm Weitkamp, ​​Oliver Bunk, Christian David: Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources . In: Nature Physics . tape 2 , no. 4 , April 2006, p. 258-261 , doi : 10.1038 / nphys265 .
7. ↑ Michael S. Chapman et al: Near-field imaging of atom diffraction gratings: The atomic Talbot effect . In: Physical Review A . tape 51 , no. 1 , January 1, 1995, p. R14-R17 , doi : 10.1103 / PhysRevA.51.R14 .
8. ↑ Stefan Gerlich among others: Quantum interference of large organic molecules . In: Nature Communications . tape 2 , April 5, 2011, p. 263 , doi : 10.1038 / ncomms1263 .
9. ^ Mathias Tomandl: Realization of optical Talbot and Talbot-Lau carpets . Diploma thesis, University of Vienna, 2010.