Fraction: Difference between revisions
No edit summary |
m rv vandalism |
||
| Line 1: | Line 1: | ||
*''For other meanings of the word 'fraction', see [[fraction (disambiguation)]]'' |
|||
A Fraction is a latin word. Frac-meaning math, and -tion, meaning demon. Created by Karl Marx in the 19th century, it is used to punish capitalistic countries |
|||
[[Image:Cake quarters.svg|thumb|right|270px|A cake with one quarter removed. The remaining three quarters are shown.]] |
|||
In [[mathematics]], a '''fraction''' (from the [[Latin]] ''fractus'', broken) is a concept of a proportional [[relation]] between an object part and the object whole. Each fraction consists of a [[denominator]] (bottom) and a [[numerator]] (top), representing (respectively) the number of equal parts that an object is divided, and the number of those parts indicated for the particular fraction. |
|||
For example, the fraction {{Fraction|3|4}} could be used to represent three equal parts of a whole object, were it divided into four equal parts. |
|||
Because it is impossible to divide something into zero equal parts, zero can never be the denominator of a fraction (see [[division by zero]]). |
|||
Similarly, a fraction with equal numerator and denominator are equal to one ({{Fraction|5|5}} = 1) and the fraction form is rarely, if ever, given as a final result. |
|||
A fraction is an example of a specific type of [[ratio]], in which the two numbers are related in a part-to-whole relationship, rather than as a comparative relation between two separate quantities. <ref>(Gellert, W. (1977). The VNR Concise Encyclopedia of Mathematics.</ref> |
|||
A fraction is a [[quotient]] of [[number]]s, the quantity obtained when the numerator is divided by the denominator. Thus {{Fraction|3|4}} represents three divided by four, in decimals 0.75, in percents 75%. The three equal parts of the cake are 75% of the whole cake. |
|||
In higher mathematics, a fraction is viewed as an element of a [[field of fractions]]. |
|||
Historically, any number that did not represent a whole was called a "fraction". The numbers that we now call "decimals" were originally called "decimal fractions"; the numbers we now call "fractions" were called "vulgar fractions", the word "vulgar" meaning "commonplace". |
|||
The numerator and denominator of a fraction may be separated by a slanting line called a '''[[solidus (punctuation)|solidus]]''' or '''[[Slash (punctuation)|slash]]''', for example {{Fraction|3|4}}, or may be written above and below a horizontal line called a '''[[vinculum (symbol)|vinculum]]''', thus: |
|||
:::<math>\textstyle\frac{3}{4}</math>. |
|||
The solidus may be omitted from the slanting style (e.g. <sup>3</sup><sub>4</sub>) where space is short and the meaning is obvious from context, for example in [[road sign]]s in some countries. |
|||
Fractions are used most often when the denominator is small. For example, it is much easier to multiply 15 by {{fraction|1|3}} than it is to multiply 15 by a decimal approximation of one third. To change a fraction to a decimal, divide the numerator by the denominator, and round off to the desired accuracy. |
|||
The word is also used in related expressions, such as ''[[continued fraction]]'' and ''[[rational function|algebraic fraction]] — see [[#Special cases|Special cases]] below. |
|||
==Forms of fractions== |
|||
===Vulgar, proper, and improper fractions=== |
|||
A '''vulgar fraction''' (or '''common fraction''') is a [[rational number]] written as one [[integer]] (the ''numerator'') [[division (mathematics)|divided]] by a non-zero integer (the ''denominator''), for example, {{Fraction|4|3}} as opposed to 1{{Fraction|1|3}}.<ref>http://www.worldwidewords.org/qa/qa-vul1.htm</ref> |
|||
A vulgar fraction is said to be a '''proper fraction''' if the absolute value of the numerator is less than the absolute value of the denominator — that is, if the absolute value of the entire fraction is less than 1 (e.g. {{Fraction|7|9}}) — but an '''improper fraction''' (US, British or Australian) or '''top-heavy fraction''' (British only) if the absolute value of the numerator is greater than or equal to the absolute value of the denominator (e.g. {{Fraction|9|7}}). |
|||
===Mixed numbers=== |
|||
A '''mixed number''' is the sum of a whole number and a proper fraction. For instance, you could have two entire cakes and three quarters of another cake. The whole and fractional parts of the number are written right next to each other: 2 + {{Fraction|3|4}} = 2{{Fraction|3|4}}. |
|||
An improper fraction can be thought of as another way to write a mixed number; in the "2{{Fraction|3|4}}" example above, imagine that the two entire cakes are each divided into quarters. Each entire cake contributes {{Fraction|4|4}} to the total, so {{Fraction|4|4}} + {{Fraction|4|4}} + {{Fraction|3|4}} = {{Fraction|11|4}} is another way of writing 2{{Fraction|3|4}}. |
|||
A mixed number can be converted to an improper fraction in three steps: |
|||
#Multiply the whole part times the denominator of the fractional part. |
|||
#Add the numerator of the fractional part to that product. |
|||
#The resulting sum is the numerator of the new (improper) fraction, and the new denominator is the same as that of the mixed number. |
|||
Similarly, an improper fraction can be converted to a mixed number: |
|||
#Divide the numerator by the denominator. |
|||
#The quotient (without remainder) becomes the whole part and the remainder becomes the numerator of the fractional part. |
|||
#The new denominator is the same as that of the original improper fraction. |
|||
===Equivalent fractions=== |
|||
Multiplying the numerator and denominator of a fraction by the same (non-zero) number results in a new fraction that is said to be '''equivalent''' to the original fraction. The word ''equivalent'' means that the two fractions have the same value. This is true because for any number ''n'', multiplying by {{Fraction|''n''|''n''}} is really multiplying by one, and any number multiplied by one has the same value as the original number. For instance, consider the fraction {{Fraction|1|2}}. When the numerator and denominator are both multiplied by 2, the result is {{Fraction|2|4}}, which has the same value as {{Fraction|1|2}}. To see this, imagine cutting the example cake into four pieces; two of the pieces together ({{Fraction|2|4}}) make up half the cake ({{Fraction|1|2}}). |
|||
For example: {{Fraction|1|3}}, {{Fraction|2|6}}, {{Fraction|3|9}}, and {{Fraction|100|300}} are all equivalent fractions. |
|||
Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. this is called '''reducing''' or '''simplifying''' the fraction. A fraction in which the numerator and denominator have no [[divisor|factor]]s in common (other than 1) is said to be '''irreducible''' or '''in lowest''' or '''simplest terms.''' For instance, {{Fraction|3|9}} is not in lowest terms because both 3 and 9 can be evenly divided by 3. In contrast, {{Fraction|3|8}} ''is'' in lowest terms — the only number that's a factor of both 3 and 8 is 1. |
|||
===Reciprocals and the "invisible denominator"=== |
|||
The '''[[Multiplicative inverse|reciprocal]]''' of a fraction is another fraction with the numerator and denominator swapped. The reciprocal of {{Fraction|3|7}}, for instance, is {{Fraction|7|3}}. |
|||
Because any number divided by 1 results in the same number, it is possible to write any whole number as a fraction by using 1 as the denominator: 17 = {{Fraction|17|1}}. (1 is sometimes referred to as the "invisible denominator.") Therefore, we can say that, except for zero, every fraction or whole number has a reciprocal. The reciprocal of 17 would be {{Fraction|1|17}}. |
|||
===Complex fractions=== |
|||
A complex fraction (or compound fraction) is a fraction in which the numerator and denominator contain a fraction. For example, {{Fraction|½|⅓}} is a complex fraction. To simplify a complex fraction, divide the numerator by the denominator, as with any other fraction: {{Fraction|½|⅓}} = {{Fraction|3|2}}. |
|||
==Arithmetic with fractions== |
|||
Fractions, like whole numbers, obey the [[commutative]], [[associative]], and [[distributive]] laws, and the rule against [[division by zero]]. |
|||
===Addition=== |
|||
The first rule of addition is that you can only add like quantities, for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below. |
|||
'''Adding like quantities''' |
|||
Imagine you have a pocket containing two quarters, and another pocket containing three quarters; in total, you have five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows: |
|||
:<math>\textstyle{\frac24+\frac34=\frac54 = 1\frac14}</math>. |
|||
[[Image:Cake_fractions.svg|thumb|right|270px|If {{Fraction|1|2}} of a cake is to be added to {{Fraction|1|4}} of a cake, the pieces need to be converted into comparable quantities, such as cake-eighths or cake-quarters.]] |
|||
'''Adding unlike quantities''' |
|||
To add fractions containing unlike quantities (eg. quarters and thirds), it is necessary to convert all amounts to like quantities. It's easy to work out the type of fraction that we need to convert to, simply by multiplying together the two denominators (bottom number) of each fraction. |
|||
Suppose we are adding quarters to thirds, then we will convert both types of fraction to <math>\textstyle{\frac14 \times \frac13=\frac1{12}}</math> (... twelfths). |
|||
Consider adding the following two quantities: |
|||
:<math>\textstyle{\frac34+\frac23}</math>. |
|||
First we convert <math>\textstyle{\frac34}</math> into twelfths by multiplying both the numerator and denominator by three: <math>\textstyle{\frac34 \times \frac33 = \frac9{12}}</math>. Note that <math>\textstyle{\frac33}</math> is equivalent to <math>\textstyle{1}</math>, which shows that <math>\textstyle{\frac34}</math> is equivalent to the resulting <math>\textstyle{\frac9{12}}</math> |
|||
Secondly, we convert <math>\textstyle{\frac23}</math> into twelfths by multiplying both the numerator and denominator by four: <math>\textstyle{\frac23 \times \frac44 = \frac8{12}}</math>. Note that <math>\textstyle{\frac44}</math> is equivalent to <math>\textstyle{1}</math>, which shows that <math>\textstyle{\frac23}</math> is equivalent to the resulting <math>\textstyle{\frac8{12}}</math> |
|||
Now we can see that: |
|||
:<math> \textstyle{\frac34+\frac23}</math> is equivalent to: |
|||
:<math>\textstyle{\frac9{12}+\frac8{12}} = \frac{17}{12} = 1\frac{5}{12} </math>. |
|||
This always works, but sometimes there is a smaller denominator that will also work (a [[least common denominator]]). For example, to add {{fraction|3|4}} + {{fraction|5|12}}, we can use the denominator 48, but we could also use the smaller denominator 12, which is the [[least common multiple]] of 4 and 12. |
|||
:<math>\textstyle{\frac34+\frac{5}{12}=\frac{9}{12}+\frac{5}{12}=\frac{14}{12}=\frac76}</math>. |
|||
===Subtraction=== |
|||
The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance, |
|||
:<math>\textstyle{\frac23-\frac12=\frac46-\frac36=\frac16}</math>. |
|||
===Multiplication=== |
|||
'''Multiplication by whole numbers''' |
|||
Considering the cake example above, if you have a quarter of the cake and you multiply the amount by three, then you end up with three quarters. We can write this numerically as follows: |
|||
:<math>\textstyle{3 \times {1 \over 4} = {3 \over 4}}</math> |
|||
As another example, suppose that five people work for three hours out of a seven hour day (ie. for three sevenths of the work day). In total, they will have worked for 15 hours (5 x 3 hours each), or 15 sevenths of a day. Since 7 sevenths of a day is a whole day and 14 sevenths is two days, then in total, they will have worked for 2 days and a seventh of a day. Numerically: |
|||
:<math>\textstyle{5 \times {3 \over 7} = {15 \over 7} = 2{1 \over 7}}</math> |
|||
'''Multiplication by fractions''' |
|||
Considering the cake example above, if you have a quarter of the cake and you multiply the amount by a third, then you end up with a twelfth of the cake. In other words, a third of a quarter (or a third times a quarter) is a twelfth. Why? Because we are splitting each quarter into three pieces, and four quarters times three makes 12 parts (or twelfths). We can write this numerically as follows: |
|||
:<math>\textstyle{{1 \over 3} \times {1 \over 4} = {1 \over 12}}</math> |
|||
As another example, suppose that five people do an equal amount work that ''totals'' three hours out of a seven hour day. Each person will have done a fifth of the work, so they will have worked for a fifth of three sevenths of a day. Numerically: |
|||
:<math>\textstyle{{1 \over 5} \times {3 \over 7} = {3 \over 35}}</math> |
|||
'''General rule''' |
|||
You may have noticed that when we multiply fractions, we multiply the two ''numerators'' (the top numbers) to make the new numerator, and multiply the two ''denominators'' (the bottom numbers) to make the new denominator. For example: |
|||
:<math>\textstyle{{5 \over 6} \times {7 \over 8} = {5 \times 7 \over 6 \times 8} = {35 \over 48}}</math> |
|||
'''Multiplication by mixed numbers''' |
|||
When multiplying mixed numbers, it's best to convert the whole part of the mixed number into a fraction. For example: |
|||
:<math>\textstyle{3 \times 2{3 \over 4} = 3 \times \left ({{8 \over 4} + {3 \over 4}} \right ) = 3 \times {11 \over 4} = {33 \over 4} = 8{1 \over 4}}</math> |
|||
In other words, <math>\textstyle{2{3 \over 4}}</math> is the same as <math>\textstyle{({8 \over 4} + {3 \over 4})}</math>, making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is <math>\textstyle{8{1 \over 4}}</math>, since 8 cakes, each made of quarters, is 32 quarters in total. |
|||
===Division=== |
|||
To divide by a fraction, simply multiply by the reciprocal of that fraction. |
|||
:<math>\textstyle{5 \div {1 \over 2} = 5 \times {2 \over 1} = 5 \times 2 = 10}</math> |
|||
:<math>\textstyle{{2 \over 3} \div {2 \over 5} = {2 \over 3} \times {5 \over 2} = {10 \over 6} = {5 \over 3}}</math> |
|||
To understand why this works, consider the following: |
|||
:Question, does |
|||
::<math>\textstyle{\frac a b \div \frac c d = \frac a b \times \frac d c}</math> |
|||
:Given/Accepted |
|||
::I. Any number divided by itself is one (e.g. <math>\textstyle{\frac d d = \frac 1 1}</math>) |
|||
::II. When a number is multiplied by one it does not change (e.g. <math>\textstyle{\frac a b \times \frac 1 1 = \frac a b \times \frac d d = \frac a b}</math>) |
|||
::III. If two fractions have common denominators, then the numerators may be divided to find the quotient (e.g. <math>\textstyle{\frac {ad}{bd} \div \frac {bc}{bd} = ad \div bc}</math>) |
|||
:Proof |
|||
::1. <math>\textstyle{\frac {a} {b} \div \frac {c} {d}}</math>, Problem |
|||
::2. <math>\textstyle{\frac {a d} {b d} \div \frac {b c} {b d}}</math>, Multiplied the first fraction by <math>\textstyle{\frac d d}</math> and the second fraction by <math>\textstyle{\frac b b}</math>, which is the same as multiplying by one, and as accepted above (I & II) does not change the value of the fraction |
|||
: |
|||
::Note: These values of one were chosen so the fractions would have a common denominator; '''bd''' is the common denominator. |
|||
: |
|||
::3. <math>\textstyle{\frac {ad}{bd} \div \frac {bc}{bd} = ad \div bc}</math>, From what was given in (III) |
|||
::4. <math>\textstyle{ad \div bc = \frac {ad}{bc}}</math>, Changed notation |
|||
::5. <math>\textstyle{\frac {ad}{bc} = \frac a b \times \frac d c }</math>, Can be seen |
|||
::6. <math>\textstyle{\frac a b \times \frac d c }</math>, Solution |
|||
: |
|||
--- |
|||
: |
|||
About 4,000 years ago Egyptians divided with fractions using slightly |
|||
different methods, using [[least common multiple]]s with [[unit fraction]]s.<ref>{{cite web|url=http://egyptianmath.blogspot.com|title=Math History|author=Milo Gardner|date=[[December 19]], [[2005]]|accessdate=2006-01-18}} See for examples and an explanation.</ref> |
|||
=== Converting repeating decimals to fractions === |
|||
Decimal numbers, while arguably more useful to work with when performing calculations, lack the same kind of precision that regular fractions (as they are explained in this article) have. Sometimes an infinite number of decimals is required to convey the same kind of precision. Thus, it is often useful to convert repeating decimals into fractions. |
|||
For most repeating patterns, a simple division of the pattern by the same amount of nines as numbers it has will suffice. For example (the pattern is highlighted in bold): |
|||
:0.'''5'''55… = 5/9 |
|||
:0.'''264'''264264… = 264/999 |
|||
:0.'''6291'''62916291… = 6291/9999 |
|||
In case zeros precede the pattern, the nines are suffixed by the same amount of zeros: |
|||
:0.0'''5'''55… = 5/90 |
|||
:0.000'''392'''392392… = 392/999000 |
|||
:0.00'''12'''1212… = 12/9900 |
|||
In case a non-repeating set of decimals precede the pattern (such as 0.1523'''987'''987987…), we must equate it as the sum of the non-repeating and repeating parts: |
|||
:0.1523 + 0.0000987987987… |
|||
Then, convert both of these to fractions. Since the first part is not repeating, it is not converted according to the pattern given above: |
|||
:1523/10000 + 987/9990000 |
|||
We add these fractions by expressing both with a common divisor... |
|||
:1521477/9990000 + 987/9990000 |
|||
And add them. |
|||
:1522464/9990000 |
|||
Finally, we simplify it: |
|||
:31718/208125 |
|||
== Special cases == |
|||
A '''[[unit fraction]]''' is a vulgar fraction with a numerator of 1 (<sup>1</sup>/<sub>7</sub>). |
|||
An '''[[Egyptian fraction]]''' is the sum of distinct unit fractions (<sup>1</sup>/<sub>3</sub>+<sup>1</sup>/<sub>5</sub>). |
|||
A '''[[dyadic fraction]]''' is a vulgar fraction in which the denominator is a [[power of two]] (<sup>1</sup>/<sub>8</sub>). |
|||
An expression that has the form of a fraction but actually represents division by or into an irrational number is sometimes called an "irrational fraction". A common example is {{fraction|π|2}}, the radian measure of a right angle. |
|||
Rational numbers are the [[quotient field]] of integers. |
|||
[[Rational function]]s are functions evaluated in the form of a fraction, where the numerator and denominator are polynomials. These rational expressions are the [[quotient field]] of the [[polynomial]]s (over some [[integral domain]]). |
|||
A '''[[continued fraction]]''' is an expression such as <math>a_0 + \frac{1}{a_1 + \frac{1}{a_2 + ...}} </math>, where the ''a<sub>i</sub>'' are integers. This is '''not''' an element of a [[quotient field]]. |
|||
The term '''[[partial fraction]]''' is used in algebra, when decomposing rational expressions (a fraction with an algebraic expression in the denominator). The goal is to write the rational expression as the sum of other rational expressions with denominators of lesser degree. |
|||
== Pedagogical tools == |
|||
In [[primary school]]s, fractions have been demonstrated through [[Cuisenaire rods]]. |
|||
See also the external links below. |
|||
==History== |
|||
:''See also: [[Egyptian fraction]]s, [[Irrational number#History|history of irrational numbers]].'' |
|||
The earliest known use of [[decimal|decimal fractions]] is ca. [[2800 BC]] as [[Ancient Indus Valley units of measurement]]. {{Fact|date=February 2007}} The [[History of Egypt|Egyptians]] used [[Egyptian fraction]]s ca. [[1000 BC]]. The [[Ancient Greece|Greeks]] used unit fractions and later continued fractions and followers of the Greek philosopher [[Pythagoras]], ca. [[530 BC]], discovered that the [[square root of two]] cannot be expressed as a fraction. In [[150 BC]] [[Jain]] mathematicians in [[History of India|India]] wrote the "Sthananga Sutra", which contains work on the theory of numbers, arithmetical operations, operations with [[fractions]]. |
|||
==In Unicode== |
|||
[[Unicode]] contains [[codepoint]]s for the fractions ¼, ½ and ¾ (1/4, 1/2 and 3/4) at <code>U+00BC</code>–<code>U+00BE</code>, and for thirds, fifths, sixths and eighths at <code>U+2153</code>–<code>U+215E</code>. Support for these may vary; they may be replaced by compatibility equivalents where appropriate. |
|||
<code>U+215F</code>, FRACTION NUMERATOR ONE (⅟) is provided for showing reciprocals; the [[solidus (punctuation)|solidus]] <code>U+2044</code>, FRACTION SLASH (⁄) is provided for composing fractions, but in practice the [[virgule]] / (at <code>U+002F</code>) is used instead. |
|||
Another way to represent fractions in an application such as Microsoft Word is to use superscript and subscript. The numerator is placed in superscript, and the denominator in subscript, with a fraction slash ( ⁄ ) between the two. For example, in the case of <sup>8</sup>⁄<sub>9</sub>: |
|||
1) Place the numerator (8) in superscript: |
|||
<sup>'''8'''</sup><br /> |
|||
2) Insert a fraction slash: |
|||
<sup>8</sup>'''⁄'''<br /> |
|||
3) Place the denominator (9) in subscript: |
|||
<sup>8</sup>⁄<sub>'''9'''</sub><br /> |
|||
== See also == |
|||
*[[Rational number]] |
|||
<!-- Hidden pending cleanup *[[Auxiliary Fractions]] An algorithm for mentally converting a fraction to a decimal value --> |
|||
== References == |
|||
<div class="references-small"> |
|||
<references/> |
|||
</div> |
|||
==External links== |
|||
* [http://www.mathfactcafe.com Curricula for Creating Fractions] |
|||
* [http://www.ericdigests.org/2000-2/fractions.htm Curricula for Teaching about Fractions] |
|||
* [http://www.ericdigests.org/2004-1/fractions.htm Teaching Fractions: New Methods, New Resources] |
|||
* [http://www.myTestBook.com Worksheets:Fractions] |
|||
* [http://www.realmath.de/Mathematik/newmathen.html Interactive and dynamic worksheets to visualize fractions] |
|||
* [http://www.kwiznet.com/p/takeQuiz.php?ChapterID=1551&CurriculumID=4&Method=Worksheet Worksheets: Identifying Fractions] |
|||
* [http://www.kwiznet.com/p/takeQuiz.php?ChapterID=1364&CurriculumID=4&Method=Worksheet Worksheets: Improper Fractions to Mixed Numbers] |
|||
* [http://www.math-lessons.ca Curricula for Teaching about Equivalent Fractions] |
|||
* [http://www.quiz-tree.com/Fractions_Practice_main.html Free online quizzes about Fractions] |
|||
* [http://www.free-ed.net/sweethaven/Math/fractions/fracs03.asp ''Endless Examples & Exercises'' for fractions] |
|||
[[Category:Fractions|*]] |
|||
[[Category:Mathematical disambiguation]] |
|||
[[Category:Elementary arithmetic]] |
|||
[[Category:Numbers]] |
|||
[[ar:كسر]] |
|||
[[bn:ভগ্নাংশ (গণিত)]] |
|||
[[be-x-old:Дробы]] |
|||
[[bg:Дроб (математика)]] |
|||
[[ca:Fracció]] |
|||
[[cs:Zlomek]] |
|||
[[da:Brøk]] |
|||
[[de:Bruchrechnung]] |
|||
[[es:Fracción]] |
|||
[[eo:Frakcio (matematiko)]] |
|||
[[fr:Fraction (mathématiques)]] |
|||
[[gd:Bloigh (matamataig)]] |
|||
[[ko:분수 (수학)]] |
|||
[[is:Almenn brot]] |
|||
[[it:Frazione (matematica)]] |
|||
[[he:שבר (מתמטיקה)]] |
|||
[[lmo:Frazziun]] |
|||
[[nl:Breuk (wiskunde)]] |
|||
[[ja:分数]] |
|||
[[no:Brøk]] |
|||
[[nn:Brøk]] |
|||
[[pl:Ułamek]] |
|||
[[pt:Fração]] |
|||
[[ru:Рациональная дробь]] |
|||
[[simple:Fraction (mathematics)]] |
|||
[[sl:Ulomek]] |
|||
[[sv:Bråk]] |
|||
[[uk:Дроби]] |
|||
[[yi:בראכטייל]] |
|||
[[zh:分數]] |
|||
Revision as of 14:34, 11 October 2007
- For other meanings of the word 'fraction', see fraction (disambiguation)
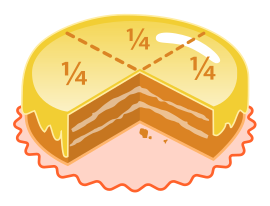
In mathematics, a fraction (from the Latin fractus, broken) is a concept of a proportional relation between an object part and the object whole. Each fraction consists of a denominator (bottom) and a numerator (top), representing (respectively) the number of equal parts that an object is divided, and the number of those parts indicated for the particular fraction.
For example, the fraction 3⁄4 could be used to represent three equal parts of a whole object, were it divided into four equal parts. Because it is impossible to divide something into zero equal parts, zero can never be the denominator of a fraction (see division by zero). Similarly, a fraction with equal numerator and denominator are equal to one (5⁄5 = 1) and the fraction form is rarely, if ever, given as a final result.
A fraction is an example of a specific type of ratio, in which the two numbers are related in a part-to-whole relationship, rather than as a comparative relation between two separate quantities. [1] A fraction is a quotient of numbers, the quantity obtained when the numerator is divided by the denominator. Thus 3⁄4 represents three divided by four, in decimals 0.75, in percents 75%. The three equal parts of the cake are 75% of the whole cake.
In higher mathematics, a fraction is viewed as an element of a field of fractions.
Historically, any number that did not represent a whole was called a "fraction". The numbers that we now call "decimals" were originally called "decimal fractions"; the numbers we now call "fractions" were called "vulgar fractions", the word "vulgar" meaning "commonplace".
The numerator and denominator of a fraction may be separated by a slanting line called a solidus or slash, for example 3⁄4, or may be written above and below a horizontal line called a vinculum, thus:
- .
The solidus may be omitted from the slanting style (e.g. 34) where space is short and the meaning is obvious from context, for example in road signs in some countries.
Fractions are used most often when the denominator is small. For example, it is much easier to multiply 15 by 1⁄3 than it is to multiply 15 by a decimal approximation of one third. To change a fraction to a decimal, divide the numerator by the denominator, and round off to the desired accuracy.
The word is also used in related expressions, such as continued fraction and algebraic fraction — see Special cases below.
Forms of fractions
Vulgar, proper, and improper fractions
A vulgar fraction (or common fraction) is a rational number written as one integer (the numerator) divided by a non-zero integer (the denominator), for example, 4⁄3 as opposed to 11⁄3.[2]
A vulgar fraction is said to be a proper fraction if the absolute value of the numerator is less than the absolute value of the denominator — that is, if the absolute value of the entire fraction is less than 1 (e.g. 7⁄9) — but an improper fraction (US, British or Australian) or top-heavy fraction (British only) if the absolute value of the numerator is greater than or equal to the absolute value of the denominator (e.g. 9⁄7).
Mixed numbers
A mixed number is the sum of a whole number and a proper fraction. For instance, you could have two entire cakes and three quarters of another cake. The whole and fractional parts of the number are written right next to each other: 2 + 3⁄4 = 23⁄4.
An improper fraction can be thought of as another way to write a mixed number; in the "23⁄4" example above, imagine that the two entire cakes are each divided into quarters. Each entire cake contributes 4⁄4 to the total, so 4⁄4 + 4⁄4 + 3⁄4 = 11⁄4 is another way of writing 23⁄4.
A mixed number can be converted to an improper fraction in three steps:
- Multiply the whole part times the denominator of the fractional part.
- Add the numerator of the fractional part to that product.
- The resulting sum is the numerator of the new (improper) fraction, and the new denominator is the same as that of the mixed number.
Similarly, an improper fraction can be converted to a mixed number:
- Divide the numerator by the denominator.
- The quotient (without remainder) becomes the whole part and the remainder becomes the numerator of the fractional part.
- The new denominator is the same as that of the original improper fraction.
Equivalent fractions
Multiplying the numerator and denominator of a fraction by the same (non-zero) number results in a new fraction that is said to be equivalent to the original fraction. The word equivalent means that the two fractions have the same value. This is true because for any number n, multiplying by n⁄n is really multiplying by one, and any number multiplied by one has the same value as the original number. For instance, consider the fraction 1⁄2. When the numerator and denominator are both multiplied by 2, the result is 2⁄4, which has the same value as 1⁄2. To see this, imagine cutting the example cake into four pieces; two of the pieces together (2⁄4) make up half the cake (1⁄2).
For example: 1⁄3, 2⁄6, 3⁄9, and 100⁄300 are all equivalent fractions.
Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. this is called reducing or simplifying the fraction. A fraction in which the numerator and denominator have no factors in common (other than 1) is said to be irreducible or in lowest or simplest terms. For instance, 3⁄9 is not in lowest terms because both 3 and 9 can be evenly divided by 3. In contrast, 3⁄8 is in lowest terms — the only number that's a factor of both 3 and 8 is 1.
Reciprocals and the "invisible denominator"
The reciprocal of a fraction is another fraction with the numerator and denominator swapped. The reciprocal of 3⁄7, for instance, is 7⁄3.
Because any number divided by 1 results in the same number, it is possible to write any whole number as a fraction by using 1 as the denominator: 17 = 17⁄1. (1 is sometimes referred to as the "invisible denominator.") Therefore, we can say that, except for zero, every fraction or whole number has a reciprocal. The reciprocal of 17 would be 1⁄17.
Complex fractions
A complex fraction (or compound fraction) is a fraction in which the numerator and denominator contain a fraction. For example, ½⁄⅓ is a complex fraction. To simplify a complex fraction, divide the numerator by the denominator, as with any other fraction: ½⁄⅓ = 3⁄2.
Arithmetic with fractions
Fractions, like whole numbers, obey the commutative, associative, and distributive laws, and the rule against division by zero.
Addition
The first rule of addition is that you can only add like quantities, for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below.
Adding like quantities
Imagine you have a pocket containing two quarters, and another pocket containing three quarters; in total, you have five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows:
- .

Adding unlike quantities
To add fractions containing unlike quantities (eg. quarters and thirds), it is necessary to convert all amounts to like quantities. It's easy to work out the type of fraction that we need to convert to, simply by multiplying together the two denominators (bottom number) of each fraction.
Suppose we are adding quarters to thirds, then we will convert both types of fraction to (... twelfths).
Consider adding the following two quantities:
- .
First we convert into twelfths by multiplying both the numerator and denominator by three: . Note that is equivalent to , which shows that is equivalent to the resulting
Secondly, we convert into twelfths by multiplying both the numerator and denominator by four: . Note that is equivalent to , which shows that is equivalent to the resulting
Now we can see that:
- is equivalent to:
- .
This always works, but sometimes there is a smaller denominator that will also work (a least common denominator). For example, to add 3⁄4 + 5⁄12, we can use the denominator 48, but we could also use the smaller denominator 12, which is the least common multiple of 4 and 12.
- .
Subtraction
The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance,
- .
Multiplication
Multiplication by whole numbers
Considering the cake example above, if you have a quarter of the cake and you multiply the amount by three, then you end up with three quarters. We can write this numerically as follows:
As another example, suppose that five people work for three hours out of a seven hour day (ie. for three sevenths of the work day). In total, they will have worked for 15 hours (5 x 3 hours each), or 15 sevenths of a day. Since 7 sevenths of a day is a whole day and 14 sevenths is two days, then in total, they will have worked for 2 days and a seventh of a day. Numerically:
Multiplication by fractions
Considering the cake example above, if you have a quarter of the cake and you multiply the amount by a third, then you end up with a twelfth of the cake. In other words, a third of a quarter (or a third times a quarter) is a twelfth. Why? Because we are splitting each quarter into three pieces, and four quarters times three makes 12 parts (or twelfths). We can write this numerically as follows:
As another example, suppose that five people do an equal amount work that totals three hours out of a seven hour day. Each person will have done a fifth of the work, so they will have worked for a fifth of three sevenths of a day. Numerically:
General rule
You may have noticed that when we multiply fractions, we multiply the two numerators (the top numbers) to make the new numerator, and multiply the two denominators (the bottom numbers) to make the new denominator. For example:
Multiplication by mixed numbers
When multiplying mixed numbers, it's best to convert the whole part of the mixed number into a fraction. For example:
In other words, is the same as , making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is , since 8 cakes, each made of quarters, is 32 quarters in total.
Division
To divide by a fraction, simply multiply by the reciprocal of that fraction.
To understand why this works, consider the following:
- Question, does
- Given/Accepted
- I. Any number divided by itself is one (e.g. )
- II. When a number is multiplied by one it does not change (e.g. )
- III. If two fractions have common denominators, then the numerators may be divided to find the quotient (e.g. )
- Proof
- 1. , Problem
- 2. , Multiplied the first fraction by and the second fraction by , which is the same as multiplying by one, and as accepted above (I & II) does not change the value of the fraction
-
- Note: These values of one were chosen so the fractions would have a common denominator; bd is the common denominator.
-
- 3. , From what was given in (III)
- 4. , Changed notation
- 5. , Can be seen
- 6. , Solution
---
About 4,000 years ago Egyptians divided with fractions using slightly different methods, using least common multiples with unit fractions.[3]
Converting repeating decimals to fractions
Decimal numbers, while arguably more useful to work with when performing calculations, lack the same kind of precision that regular fractions (as they are explained in this article) have. Sometimes an infinite number of decimals is required to convey the same kind of precision. Thus, it is often useful to convert repeating decimals into fractions.
For most repeating patterns, a simple division of the pattern by the same amount of nines as numbers it has will suffice. For example (the pattern is highlighted in bold):
- 0.555… = 5/9
- 0.264264264… = 264/999
- 0.629162916291… = 6291/9999
In case zeros precede the pattern, the nines are suffixed by the same amount of zeros:
- 0.0555… = 5/90
- 0.000392392392… = 392/999000
- 0.00121212… = 12/9900
In case a non-repeating set of decimals precede the pattern (such as 0.1523987987987…), we must equate it as the sum of the non-repeating and repeating parts:
- 0.1523 + 0.0000987987987…
Then, convert both of these to fractions. Since the first part is not repeating, it is not converted according to the pattern given above:
- 1523/10000 + 987/9990000
We add these fractions by expressing both with a common divisor...
- 1521477/9990000 + 987/9990000
And add them.
- 1522464/9990000
Finally, we simplify it:
- 31718/208125
Special cases
A unit fraction is a vulgar fraction with a numerator of 1 (1/7).
An Egyptian fraction is the sum of distinct unit fractions (1/3+1/5).
A dyadic fraction is a vulgar fraction in which the denominator is a power of two (1/8).
An expression that has the form of a fraction but actually represents division by or into an irrational number is sometimes called an "irrational fraction". A common example is π⁄2, the radian measure of a right angle.
Rational numbers are the quotient field of integers. Rational functions are functions evaluated in the form of a fraction, where the numerator and denominator are polynomials. These rational expressions are the quotient field of the polynomials (over some integral domain).
A continued fraction is an expression such as , where the ai are integers. This is not an element of a quotient field.
The term partial fraction is used in algebra, when decomposing rational expressions (a fraction with an algebraic expression in the denominator). The goal is to write the rational expression as the sum of other rational expressions with denominators of lesser degree.
Pedagogical tools
In primary schools, fractions have been demonstrated through Cuisenaire rods.
See also the external links below.
History
- See also: Egyptian fractions, history of irrational numbers.
The earliest known use of decimal fractions is ca. 2800 BC as Ancient Indus Valley units of measurement. [citation needed] The Egyptians used Egyptian fractions ca. 1000 BC. The Greeks used unit fractions and later continued fractions and followers of the Greek philosopher Pythagoras, ca. 530 BC, discovered that the square root of two cannot be expressed as a fraction. In 150 BC Jain mathematicians in India wrote the "Sthananga Sutra", which contains work on the theory of numbers, arithmetical operations, operations with fractions.
In Unicode
Unicode contains codepoints for the fractions ¼, ½ and ¾ (1/4, 1/2 and 3/4) at U+00BC–U+00BE, and for thirds, fifths, sixths and eighths at U+2153–U+215E. Support for these may vary; they may be replaced by compatibility equivalents where appropriate.
U+215F, FRACTION NUMERATOR ONE (⅟) is provided for showing reciprocals; the solidus U+2044, FRACTION SLASH (⁄) is provided for composing fractions, but in practice the virgule / (at U+002F) is used instead.
Another way to represent fractions in an application such as Microsoft Word is to use superscript and subscript. The numerator is placed in superscript, and the denominator in subscript, with a fraction slash ( ⁄ ) between the two. For example, in the case of 8⁄9:
1) Place the numerator (8) in superscript:
8
2) Insert a fraction slash:
8⁄
3) Place the denominator (9) in subscript:
8⁄9
See also
References
- ^ (Gellert, W. (1977). The VNR Concise Encyclopedia of Mathematics.
- ^ http://www.worldwidewords.org/qa/qa-vul1.htm
- ^ Milo Gardner (December 19, 2005). "Math History". Retrieved 2006-01-18.
{{cite web}}: Check date values in:|date=(help) See for examples and an explanation.
External links
- Curricula for Creating Fractions
- Curricula for Teaching about Fractions
- Teaching Fractions: New Methods, New Resources
- Worksheets:Fractions
- Interactive and dynamic worksheets to visualize fractions
- Worksheets: Identifying Fractions
- Worksheets: Improper Fractions to Mixed Numbers
- Curricula for Teaching about Equivalent Fractions
- Free online quizzes about Fractions
- Endless Examples & Exercises for fractions






































