Cross-polytope

In geometry, a cross-polytope, or orthoplex, or hyperoctahedron, is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope consist of all permutations of (±1, 0, 0, …, 0). The cross-polytope is the convex hull of its vertices. (Note: some authors define a cross-polytope only as the boundary of this region.)

The n-dimensional cross-polytope can also be defined as the closed unit ball in the ℓ₁-norm on Rⁿ:

$\{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}.$

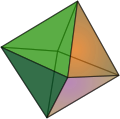
In 1 dimension the cross-polytope is simply the line segment [−1, +1], in 2 dimensions it is a square (or diamond) with vertices {(±1, 0), (0, ±1)}. In 3 dimensions it is an octahedron—one of the five regular polyhedra known as the Platonic solids. Higher-dimensional cross-polytopes are generalizations of these.

2 dimensions square		3 dimensions octahedron		4 dimensions 16-cell

The cross-polytope is the dual polytope of the hypercube. The 1-skeleton of a n-dimensional cross-polytope is a Turán graph T(2n,n).

4 dimensions

The 4-dimensional cross-polytope also goes by the name hexadecachoron or 16-cell. It is one of six regular convex polychora. These polychora were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.

Higher dimensions

In n > 4 dimensions there are only three regular polytopes: the simplex, the hypercube, and the cross-polytope, of which the last two are duals. The simplex is self-dual.

The n-dimensional cross-polytope has 2n vertices, and 2ⁿ facets (n−1 dimensional components) all of which are n−1 simplices. The vertex figures are all n−1 cross-polytopes. The Schläfli symbol of the cross-polytope is {3,3,…,3,4}.

The number of k-dimensional components (vertices, edges, faces, …, facets) in an n-dimensional cross-polytope is given by (see binomial coefficient):

$2^{k+1}{n \choose {k+1}}$

A two dimensional graph of the edges of the n-dimensional cross-polytope can be constructed by drawing 2n vertices on a circle and connecting all pairs of vertices except for vertices exactly on opposite sides of the circle. (These unattached pairs represent the vertex pairs on opposite directions of one coordinate axis of the polytope.) To put this more abstractly, the graph is the complement of a matching of n edges.

Cross-polytope elements

n	Graph	Name(s) Schläfli symbol	Coxeter-Dynkin diagrams	Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	7-faces	8-faces
1		Line segment 1-cross-polytope	{}	2
2		Bicross square 2-cross-polytope	{4}	4	4
3		Tricross octahedron 3-cross-polytope	{3,4}	6	12	8
4		Tetracross 16-cell hexadecachoron 4-cross-polytope	{3,3,4}	8	24	32	16
5		Pentacross triacontakaidi-5-tope 5-cross-polytope	{3,3,3,4}	10	40	80	80	32
6		Hexacross hexacontatetra-6-tope 6-cross-polytope	{3,3,3,3,4}	12	60	160	240	192	64
7		Heptacross hecticosiocta-7-tope 7-cross-polytope	{3,3,3,3,3,4}	14	84	280	560	672	448	128
8		Octacross dihectapentacontahexa-8-tope 8-cross-polytope	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256
9		Enneacross pentahectadodeca-9-tope 9-cross-polytope	{3,3,3,3,3,3,3,4}	18	144	672	2016	4032	5376	4608	2304	512

See also

• List of regular polytopes

Reference

• Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed. ed.). New York: Dover Publications. pp. 121–122. ISBN 0-486-61480-8. {{cite book}}: |edition= has extra text (help) p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)

External links

• Weisstein, Eric W. "Cross polytope". MathWorld.
• Polytope Viewer (Click <polytopes...> to select cross polytope.)
• Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.