Wikipedia:Reference desk/Mathematics

Welcome to the mathematics section
of the Wikipedia reference desk.

skip to bottom

Select a section:

• Computing
• Entertainment
• Humanities
• Language
• Mathematics
• Science
• Miscellaneous
• Archives

Want a faster answer?

Main page: Help searching Wikipedia

   

How can I get my question answered?

• Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
• Post your question to only one section, providing a short header that gives the topic of your question.
• Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
• Don't post personal contact information – it will be removed. Any answers will be provided here.
• Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
• Note:
  • We don't answer (and may remove) questions that require medical diagnosis or legal advice.
  • We don't answer requests for opinions, predictions or debate.
  • We don't do your homework for you, though we'll help you past the stuck point.
  • We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

• The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

See also:

• Teahouse
• Help desk
• Village pump
• Help manual

August 30

Operation of adding a fraction and its reciprocal

For nonzero $a$ and $b$, define $a\odot b={a \over b}+{b \over a}$. It seems to be that for $k\geq 2$ and positive integers $n_{1},n_{2},\ldots ,n_{k}$, if the expression

$n_{1}\odot n_{2}\odot \cdots \odot n_{k}$,

parenthesized in any way, is an integer, then it is 2. Is this true? —Bkell (talk) 05:10, 30 August 2008 (UTC)

Hmm, after thinking about this as adding a fraction and its reciprocal (which didn't occur to me until I had to come up with a heading for this section), I see why it's true. Suppose $x+{1 \over x}=k$ for some integer $k$. Then $x={k\pm {\sqrt {k^{2}-4}} \over 2}$, which isn't going to be rational unless $k=2$. Since the $\odot$ operation can produce only rational numbers if we start with integers, we'll never get any integer answer except 2. —Bkell (talk) 05:39, 30 August 2008 (UTC)

Verhoeff algorithm

I'm trying to use this for some hobbyist thing so I've been looking for an online or offline for Windows easy to use implementation. First came across this [1] which I presume is precomputed check digits for up to 5 digits which is fine since I only need 4. But I wanted to check it and eventually found this [2] (which I later realised is link to on the wiki article). Trouble is, the results don't tend to agree. Could someone who can actually understand the article (or already knows the algorithm) tell me which one is producing correct results, if any? Alternatively links to any offline or online implementation that works is fine Nil Einne (talk) 09:39, 30 August 2008 (UTC)

Affine curvature

Is Affine curvature defined when the speed of the curve is zero? My instinct says it isn't, but I'd like a second opinion. Tompw (talk) (review) 11:52, 30 August 2008 (UTC)

The speed of a curve is a property of the parametrisation, the curvature shouldn't depend on the parametrisation so it will still be defined, you can just pick a different parametrisation in order to calculated it (parametrise by arc length, perhaps, then you know the speed will always be positive). --Tango (talk) 18:40, 30 August 2008 (UTC)

Actually, having a good notion of Eucldiean curvature generally does depend on being able to select a parameterization for which, at least, the speed is nonzero. The affine curvature requires slightly more than this. In order for the affine curvature to be well-defined, a plane curve must support a parameterization in which the velocity and acceleration are linearly independent. Ultimately the definition can be made independent of the parameterization, or at least dependent only on the preferred parameterization with respect to special affine arclength, but the basic non-degeneracy requirement remains. siℓℓy rabbit (talk) 23:55, 30 August 2008 (UTC)

Range and Domain

please could someone answer how to find the range domain and inverse of y=x^3. i tried finding the answer, i got the range as negative infinity and infinity. according to me i suppose that is correct, but somewhere i read the answer as 'R' which is real numbers i guess. which i couldn't understand, someone please tell me how does it become real number? its not affinely extended real number which is R with a dash on top, but it is just R. so please explain. —Preceding unsigned comment added by 128.211.240.72 (talk) 20:07, 30 August 2008 (UTC)

Strictly speaking, the domain could be any number of things, but in context, the expected answer is probably $\mathbb {R}$, the set of real numbers. With this domain, the range is also $\mathbb {R}$, since the cube of a real number is always a real number, and every real is the cube of some real. I'll leave working out the inverse function as an exercise for the reader. Feel free to ask here again if you have more questions not answered in the articles I've linked. Algebraist 20:13, 30 August 2008 (UTC)

$(-\infty ,\infty )$ (or $-\infty <x<\infty$) is just the whole of the real numbers, so you're absolutely right. --Tango (talk) 22:12, 30 August 2008 (UTC)

For the record, there's no problem with having the extended real number system, $\mathbb {R} \cup \left\{-\infty ,\infty \right\}$ as the domain either, so your answer is definitely correct. But as Algebraist pointed out, a person asking "what is the domain of $y=x^{3}$?" most likely means "what is the largest subset of $\mathbb {R}$ that can be the domain of a function $x\rightarrow y$ given by the rule $y=x^{3}$?". -- Jao (talk) 12:26, 31 August 2008 (UTC)

I think the poster saw the answer $\scriptstyle (-\infty ,\infty )$ somewhere and interpreted it to mean $\scriptstyle \{-\infty ,\infty \}$. He/she then saw the answer $\scriptstyle \mathbb {R}$ elsewhere, and did not realize that that is what $\scriptstyle (-\infty ,\infty )$ means. So the short answer is that $\scriptstyle (-\infty ,\infty )$ is the set of real numbers. The more important lesson is that it is no good to know the answer is you don't know what it means. Oded (talk) 17:02, 31 August 2008 (UTC)

August 31

Problem in a proof

I was reading about Ramsey theory on this page and am stuck on a seemingly trivial point in the proof of Van der Waerden's theorem (It is Theorem 6 in the pdf, page 26 or 28). The problem is this: First we define a function $\chi :\{1,\cdots M(M'+1)\}\rightarrow \{1,\cdots r\}$. Then the writer claims that this induces a function $\chi ':\{1,\cdots M'\}\rightarrow \{1\dots r^{M}\}$ such that the following condition holds:

$\chi '(k)=\chi '(k')\iff \chi (kM+j)=\chi (k'M+j)\forall j\in \{1\cdots M\}$

What I don't understand is how is the existence of such a function guaranteed. Why is $r^{M}$ large enough to accomodate the various values that numbers from 1 to M' will take while retaining the imposed condition. (Earlier he had stated that M' was the Van der Waerden number for l and $r^{M}$ i.e. if numbers from 1 to M' are assigned into classes from 1 to $r^{M}$ at least l numbers would fall in the same class. I do not know whether this has anything to do with my question.)

I would appreciate any help. Thanks.--Shahab (talk) 07:30, 31 August 2008 (UTC)

Here's my impression of it: he wants you to take the long sequence of colors in blocks, and treat each smaller sequence of colors within a block like a single more complicated color. So, say the integers 1-20 were colored with the numbers 1-3. We could have, for instance, 13112131221213233312. You could imagine this instead as coloring the integers 1-5 with the numbers 1111-3333 where the digits are all 1's, 2's and 3's. In other words, (1311)(2131)(2212)(1323)(3312). Since there are 3^4 colors of that form, we could relabel them with the numbers 1-81. Two integers are colored the same precisely when their blocks of colors are the same, which in symbols is what he wrote. He also seems to leave off a bit at the beginning of the original sequence, since he doesn't need all of it. You'll notice his condition only applies to terms in the original sequence with index at least M+1. Black Carrot (talk) 23:45, 2 September 2008 (UTC)

Sine Law Ambiguous Case

Hello. Are imaginary solutions possible if a < b sin A like if the discriminant in the quadratic formula is negative? 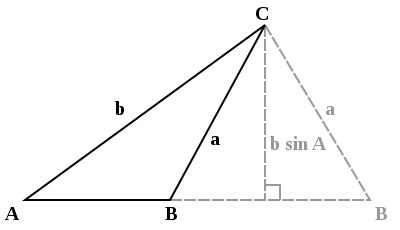Thanks in advance. --Mayfare (talk) 19:20, 31 August 2008 (UTC)

I do not understand your question. a cannot be smaller than b sin A. Secondly what quadratic formula? I do not see any quadratic formula. I think you assumed that other people know what you know about the problem. If there is a method of determining a than you may have to show us. 202.147.44.80 (talk) 22:56, 31 August 2008 (UTC)

OK. I am assuming that you are looking at the equation $\scriptstyle \sin B=(b/a)\sin A$ which comes from the sine law. If $\scriptstyle a<b\sin A$ then there are no real solutions for B to this equation. Yes, there would be solutions in the complex plane, but they would not be of interest if you are looking at the geometric problem (though they would probably be relevant to some appropriate geometric generalization). And you are right, that this is analogous to the situation with the quadratic formula, in the sense that many equations that have no real solutions will have complex solutions. Oded (talk) 23:02, 31 August 2008 (UTC)

Geometrical problems often lead to equations where only the real solutions make sense. The equation sin x = a has real solutions when a is a real number and |a| ≤ 1, say, a = 1/2. Otherwise it has non-real complex solutions that cannot be interpreted as angles. The equation sin x = 2 has a solution x ≈ 1.571 + 1.317i. Bo Jacoby (talk) 11:39, 1 September 2008 (UTC).

September 1

Distance along sine curve

Is there any way to find the distance between two given points on a sine or cosine curve (or any continuous segment of a trigonometric curve, for that matter) along the length of the curve (much like evaluating the length of an arc of a circle)? On a similar note, how can the length of a segment of a conic section curve, e.g. a parabola or an ellipse be evaluated?Leif edling (talk) 06:14, 1 September 2008 (UTC)

Our article on arc length covers this fairly well, I think. Briefly, the usual way is to consider the integral

$\int _{\gamma }{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}dt$

where t is a parameter along the curve. Along a sine curve, we could use x as the independent variable and :$y=\sin(x)$ as the dependent variable for

$\int _{x_{0}}^{x_{1}}{\sqrt {1+\cos ^{2}(x)}}\,dx$

Best, RayAYang (talk) 06:23, 1 September 2008 (UTC)

Perfect square trinomial

What is the value of "c" so, x² + x + c, is a perfect square trinomial? Wikiuser146 (talk) 18:25, 1 September 2008 (UTC)

See completing the square. Algebraist 18:29, 1 September 2008 (UTC)

Is the answer possible? Wikiuser146 (talk) 18:34, 1 September 2008 (UTC)

Yes. Algebraist 18:35, 1 September 2008 (UTC)

Is the answer "1"? —Wikiuser146 (talk • contribs) 18:38, 1 September 2008 (UTC)

No, (x + 1)² = x² + 2x + 1 ≠ x² + x + 1 --El aprendelenguas (talk) 18:48, 1 September 2008 (UTC)

Ignore the "c" and use the other two terms to determine the binomial. Then expand the binomial and determine c. --Bowlhover (talk) 23:44, 1 September 2008 (UTC)

Or just find the value of c for which the discriminant is zero. siℓℓy rabbit (talk) 00:00, 2 September 2008 (UTC)

10 marbles

Resolved

Consider a paper bag full of 10 marbles, 9 red and 1 blue. Suppose 10 people line up and one-by-one randomly pick a marble from the paper bag. The farther your position from the front of the line, the more likely someone in front of you will take the blue marble; however, the longer the blue marble goes unpicked, the greater the chances are of picking it (to the point that, if the blue marble remains in the bag after 9 people, the probability of the last person picking it is 100%). Considering all this, which position in line (from 1st to 10th) has the greatest probability of picking the blue marble? Or are they all somehow equal? Thanks!--El aprendelenguas (talk) 18:44, 1 September 2008 (UTC)

They are equal.

The first person picks the blue marble with a probability of 1/10.

The second one picks it with chance of 1/9 provided that the first one picked the red one (for which the chance is 9/10), so the final chance for the second person to pick the blue marble is 9/10 × 1/9 = 1/10.

The third one picks it with chance of 1/8 provided that the first one and the second both picked red marbles (for which chances are 9/10 and 8/9, respectively), so the final chance for the third person to pick the blue marble is (9/10 × 8/9) × 1/8 = 1/10.

For n-th person it is (9/10 × 8/9 × ... × (11-n)/(12-n)) × 1/(11-n) = (11-n)/10 × 1/(11-n) = 1/10.

CiaPan (talk) 19:33, 1 September 2008 (UTC)

Aaaah, that makes sense. Thank you very much!--El aprendelenguas (talk) 20:03, 1 September 2008 (UTC)

Put it in more general way. Let's mark our marbles with natural numbers (1 through 10) and let ten people pick them in order.

The first person picks one of them, and each marble has the same chance to be picked. So it is equally probable to get each of numbers 1 through 10 as first.

Then the second person picks a marble — and each of them has equal chance to be picked. So it is equally probable to get any sequence of two different numbers, from (1,2), (1,3), (1,4) and so on through (1,10), (2,1), (2,3), ... (2,10), ... (9,10), (10,1), (10,2), ... (10,9).

Proceeding this way we'll eventually get this result: each of 10!=3628800 permutations of ten numbers is equally probable as a result of this experiment.

Now let's assume all marbles are red, except the one marked with 3, which is blue. There are 9!=362880 permutations with 3 as the first number picked, 9! permutations with 3 at the second place, and similarly 9! permutations with 3 at any chosen position. So every person in a queue has the same chance to pick a marble 3, that is the blue one.

CiaPan (talk) 18:57, 2 September 2008 (UTC)

Here is yet another approach, this one based on intuitive reductio ad absurdum. Let's assume we have 8 red marbles, a blue one and a green one. Suppose the probability of picking the blue marble by the n-th person differs from 1/10, say it is a bit greater than 1/10. This implies the chance of picking some other marbles must be less than 1/10. Suppose it is the green one which has reduced chance to take n-th place.

But what reason could cause such a difference? The chance of blind-picking any marble does not depend on its color! So why should a blue marble be 'privileged' to n-th place?
What result would we get, if we take 9 red marbles and the green one? Will the green marble intercept the blue marble's privilege? (If so, how does it know the blue one is out of the game?) Or rather it will remain on its <1/10 probability level in respect to the n-th place? (If so, which red marble would get its "n-th probability" raised?)

It's obvious all possibilities presented above are nonsense: the chances to get any particular marble on the chosen position are equal, and can not depend on marking one or all of them with distinct colors.
CiaPan (talk) 18:35, 3 September 2008 (UTC)

bernoulli trials with unique p

A Bernoulli Trial, which results in a Binomial Distribution, results when the events are independent and with the same probability. What is the distribution called when the probabilities of the independent events are not equal? And are there any online applets to let you graph the distribution? I would imagine those combinatorics would be a nightmare to calculate without a program. Thanks. --VectorField (talk) 20:06, 1 September 2008 (UTC)

I'm not sure I understand the question. The binomial distribution has one of two possible outcomes for each among a succession of independent trials. One of these outcomes occurs with probability p and the other with probability 1 − p. (Of course, p and 1 − p need not be equal.) In general, what you are asking seems to be something like the following: what if the probability p changes in some definite deterministic way from trial to trial. In that case, you may want to look at multinomial distribution. This isn't a complete answer, but may help to point you in the right direction. siℓℓy rabbit (talk) 20:46, 1 September 2008 (UTC)

I am looking for a two-outcome distribution where the p is different from trial to trial. For example, a distribution of the number of heads when I flip four unfair coins with heads probabilities of (30%, 40%, 60%, 70%). It would not be the multinomial distribution, which is even more far afield of this than a binomial distribution. Are there any applets which would generate such a distribution. Even though I could work out the combinatorics of such a problem, I am working with a large data set (>30 trials), so I am looking for an applet that would do it for me. --VectorField (talk) 21:02, 1 September 2008 (UTC)

You can use multinomial distribution for this provided all coins are tossed equally often. Take one trial to be the toss of each of the four coins and the outcome to be the number of heads. Taemyr (talk) 23:52, 1 September 2008 (UTC)

The OP seems to be looking to find a way to actually calculate this distribution. Setting the p's of the multinomial distribution to the results of the calculation doesn't actually accomplish anything. With a data set that size, your best bet would be to use the Monte Carlo method. That is, running simulations. --Thegoodearth (talk) 00:05, 2 September 2008 (UTC)

Consider the set of numbers from 1 through n,

$\mathbf {n} =\{1\cdots n\},$

and the set of i-subsets of $\mathbf {n}$,

${\tbinom {\mathbf {n} }{i}}=\{S:(S\subseteq \mathbf {n} )\land (|S|=i)\}$

then the probability of obtaining i hits out of n trials, when the kth hit probability is p_k, is

$\sum _{S\in {\tbinom {\mathbf {n} }{i}}}\prod _{k\in \mathbf {n} }((k\in S)p_{k}+(k\notin S)(1-p_{k}))$

where the Iverson bracket $(k\in S)$ is 1 if the number k is a member the set S, and 0 otherwise. So the expression $(k\in S)p_{k}+(k\notin S)(1-p_{k})$ is $p_{k}\,$ if $k\in S$ and $1-p_{k}\,$ if $k\notin S.$

If all p_k are equal to p you get the binomial distribution as a special case.

$\sum _{S\in {\tbinom {\mathbf {n} }{i}}}\prod _{k\in \mathbf {n} }((k\in S)p+(k\notin S)(1-p))=\sum _{S\in {\tbinom {\mathbf {n} }{i}}}p^{i}(1-p)^{n-i}={\tbinom {n}{i}}p^{i}(1-p)^{n-i}.$

Bo Jacoby (talk) 11:14, 2 September 2008 (UTC).

This is a problem that is easily solved by generating functions. The probability of getting $i$ heads equals the coefficient of $x^{i}$ in the formal product

$\prod _{k=1}^{n}(p_{k}x+(1-p_{k}))$.

The product can be computed automatically by any computer algebra system, some of which are available as free software. For example, with the probabilities 30%, 40%, 60%, 70% we get

$(0.3x+0.7)(0.4x+0.6)(0.6x+0.4)(0.7x+0.3)=0.0504x^{4}+0.2484x^{3}+0.4024x^{2}+0.2484x+0.0504$

indicating for example that the probability of getting 3 heads is 24.84 %. 84.239.160.166 (talk) 19:50, 3 September 2008 (UTC)

That is beautyful. I wonder why the generating function $(1-p+px)^{n}$ is not found in the article on the binomial distribution. Bo Jacoby (talk) 10:29, 4 September 2008 (UTC).

That is an example of a probability-generating function. This suggests an improvement to the probability distribution template for the discrete case (where type=mass). Good catch. Baccyak4H (Yak!) 13:11, 4 September 2008 (UTC)

September 2

exponential increase

Since the sexes come in pairs it is quite possible the binary base system of counting was known many centuries prior to computers. Aside from that possibility I have two parents and they have two parents or $p=2^{n}$, where $n$ is the number of prior generations. If $p$ is the minimum size of the population, assuming persons in any generation have parents from only and do not share any parents from the previous generation, at some point $p$ will become so large as to be impossible. So can one assume this is the limit for number of previous generations? —Preceding unsigned comment added by 71.100.6.185 (talk) 13:36, 2 September 2008 (UTC)

No, the limit on the generations wouldn't fit the fossil record (it would be far too small). The apparently impossible population size is because of your assumption that nobody shares parents, that assumption is clearly not true and in fact becomes more and more inaccurate the more generations back you go (basically, you've assumed that no-one alive today is related to anyone else alive today, going back to further generations means taking into account more and more distant relationships). If you go far enough back, everyone shares the same ancestors (see Identical ancestors point), and that number of ancestors is far far smaller than doubling the population n times would suggest (it's actually going to be far smaller than the current population, since the population has been growing over time). --Tango (talk) 13:57, 2 September 2008 (UTC)

Yes, but if you reduce your base from 2 to 1.1 the population still reaches max at only ~13,000 years in the past. What is the equation you are using? —Preceding unsigned comment added by 71.100.6.185 (talk) 00:10, 3 September 2008 (UTC)

No exponential curve is going to be a good fit, regardless of the base. Your number of ancestors in a given generation grows exponentially at first, but then reaches a saturation point and levels off. Eventually it will actually start decreasing. It probably looks something like a logistic function. Most apparently exponential growth patterns are really the leading end of a logistic curve. -- BenRG (talk) 11:48, 3 September 2008 (UTC)

September 3

hilbart space

what is Hilbert Space in metric space? —Preceding unsigned comment added by Debadhi (talk • contribs) 05:55, 3 September 2008 (UTC)

All Hilbert spaces are metrizable (by definition).

Topology Expert (talk) 10:02, 3 September 2008 (UTC)

for a proof

Is any element of a Hilbert Space complet? —Preceding unsigned comment added by Debadhi (talk • contribs) 06:02, 3 September 2008 (UTC)

Could you please make your question clearer? If you are asking whether any element of a Hilbert space is complete then it is meaningless; an element can not be complete but a space can.

Topology Expert (talk) 09:57, 3 September 2008 (UTC)

Similarly, if I have interpreted your question correctly, all Hilbert spaces are complete by definition. Perhaps you should have a look at Hilbert space for discussion on these spaces.

Topology Expert (talk) 10:03, 3 September 2008 (UTC)

Complicated Maths Question

Here's the original question: The Harvard University Examination Board dispatches copies of an examination question paper yearly to schools in 50,20 or 5 copies. The delivery instructions produced by the board's computer are in the form of x/y/z meaning x packets of 50 copies, y packets of 20 copies and z packet of 5 copies. The following rules are observed during the dispatch: one copy of the question paper is supplied to each candidate each school receives at least 3 extra copies. the no. of question papers sent to schools must be as small as possible, satisfying the two above rules. once the number of question papers is determined, the board dispatches the minimum number of packets to the school.

The question: in 1999, the school receives 11 packets of papers for 1 subject. calculate the no. of copies received in that year.

The question seems to have one rule lacking as the model answer is 385 but mine is 55(all the packets may only contain 5 papers). —Preceding unsigned comment added by Invisiblebug590 (talk • contribs) 07:28, 3 September 2008 (UTC)

Your answer violates the rule that the number of packets must be minimized. If they wanted to send 55 papers, they'd send it as 50+5 (2 packets) not 5+5+5+5+5+5+5+5+5+5+5 (11 packets) --tcsetattr (talk / contribs) 07:45, 3 September 2008 (UTC)

385 may be the least number of copies that require 11 packets if packaged to minimise number of packets, but it it obviously not the only number of copies that the school could have received - another possibility is 550 papers in 11 packets of 50. Unless it specifies "least number of copies", I think the question is ambiguous. Gandalf61 (talk) 10:54, 3 September 2008 (UTC)

You are correct. The full list of answers requiring 11 packets at a minimum are: 385, 415, 430, 445, 460, 475, 490, 505, 520, 550; With 385 being the smallest of the answers. Anythingapplied (talk) 15:27, 3 September 2008 (UTC)

A bit of a strange question...

Take this example problem: If a 10 foot tall ladder leans against a wall, and the base of the ladder is 5 feet away from the wall, how far up the wall does the ladder go? The answer using Pythagoras' theorem is:
$5^{2}+b^{2}=10^{2}\,$
$b={\sqrt {100-25}}=5{\sqrt {3}}\,$
Now the square root gives a positive and a negative answer. In this real world example it is quite obvious that the one we want--the correct answer--is the positive one. My question is with things like this where we must pick between 2 or perhaps more mathematically valid answers is there a more "formal" way of deciding of which one to use. For example, in a case where imagining the problem in our heads is difficult common sense may not be of much help to us. --212.120.246.239 (talk) 15:06, 3 September 2008 (UTC)

It really depends on the context. In a physical problem, there are instances where negative solutions are meaningless, or where non-integer solutions are not acceptable.

Consider a family in which the number of children is X. If two less than the number of children, multiplied by five less than three times the number of children, equals 4, then we've got a quadratic equation: $(x-2)(3x-5)=4$, which is equivalent to $3x^{2}-11x+6=0$. Solving this quadratic equation, we obtain two answers: $x=3$ and $x={\frac {2}{3}}$. The latter answer is clearly inapplicable to the problem.

On the other hand, if we're just solving the equation $(x-2)(3x-5)=4$, with no thought of application, then we'll keep both answers. The key is in your question: "is there a ... way of deciding which one to use?" If there's an application, then it may provide constraints on acceptable solutions. Determining which solutions apply and which do not apply to a particular application is part of the challenge of applied mathematics. I don't know of a general method, simply because applications can vary widely. Sometimes, a solution that seems meaningless in a physical problem will lead to new physical ideas. If memory serves, the existence of Black holes was predicted when some equations "blew up", with an infinite term appearing, which was at first assumed to be extraneous. I know there are other examples of this sort of thing, but that's the one that comes to mind just now.

In other cases, simply checking whether our solution satisfies the original problem will lead to some solution being thrown out. Consider: ${\frac {x+1}{x-2}}=x+9+{\frac {3}{x-2}}$. If we multiply both sides by $x-2$, we obtain another quadratic equation: $x+1=x^{2}+7x-15$. We can solve this to obtain $x=-8$ or $x=2$, but the latter solution clearly does not work in the original problem. (We could have caught this earlier by being more careful, and noting that $x\neq 2$ is implied by the original equation.)

I realize this isn't quite a succinct answer, but I hope it helps illuminate your question somewhat. -GTBacchus^(talk) 16:02, 3 September 2008 (UTC)

Whenever you use mathematics for a real world problem, you have to come up with a mathematical model that is basically a way of converting your real world concepts into mathematical concepts. In your example you are modelling lengths as non-negative real numbers. The fact that they are non-negative is part of the model, so acts as a constraint to the mathematics. There is no absolute way of working out what constraints you will need when modelling any given situation, coming up with a model is the first, any often hardest, part of solving the problem (once you have a good model all that's left is often basic arithmetic). --Tango (talk) 18:00, 3 September 2008 (UTC)

• (ec) You ask 'how FAR UP the wall does the ladder go?', so you define a vertical axis, along which you measure the 'height', and the axis is oriented upwards. The negative result then means simply a point below the floor. An algebraic equation, which you used to express the problem, does not contain a condition of 'only positive ordinate allowed', so the Pythagorean formula describes two triangles: the one between the ladder, the floor and the wall, and the other one, which is the reflection of it in respect to the floor. Eventually you get two solutions, defining the upper and the lower vertex of the upper and the lower triangle, respectively. --CiaPan (talk) 18:11, 3 September 2008 (UTC)

• In 'formal' mathematics the values which satisfy the equation are the ones that are in the problem's domain. Going from a real world problem to the mathematics involves deciding the domain of the variables as well as the equations that apply to them. For number of children the domain would be the non-negative integers (except in statistics of course!). If you want only heights and don't allow negative heights then you can either have a condition that the height is greater than or equal to zero and use the domain of real numbers (but of course negative ones won't satisfy the condition), or else you could use a domain consisting only of the non-negative reals. Dmcq (talk) 18:46, 3 September 2008 (UTC)

• The quadratic equation is a tool you can use to find out the answer you want. But the tool does not know the context of the question, so it just spits out all the possible answers that could, in some context, satisfy it. An analogy is this question: How do I get from A to B? Well, the options include walking, crawling, driving a car, swimming, flying by plane, taking a bus, train, taxi etc etc etc. All those answers could apply to specific As and Bs. But if your A was your kitchen and your B was your bedroom, then only one of these options (walking) would actually apply, and you'd know which one it was. (Ok, maybe crawling could be an option, too, but not the others). -- JackofOz (talk) 01:26, 5 September 2008 (UTC)

Peanut shaped

Is there a name for that geometric shape? If so, what is it?--Honeymane_{Heghlu meH QaQ jajvam} 22:07, 3 September 2008 (UTC)

As far as I know, there isn't a specific name for a "peanut shaped" object. If you draw a Cassini oval with b/a slightly greater than 1 - say between 1.1 and 1.2 - then you get a two-lobed curve that resembles the cross-section of a peanut. Gandalf61 (talk) 11:02, 4 September 2008 (UTC)

Really? I was under the impression that there was names for everything. Oh well.--Honeymane_{Heghlu meH QaQ jajvam} 20:48, 4 September 2008 (UTC)

This Prolate spheroid certainly looks pretty much like a peanut to me. I got linked to the article from Rugby ball because, well, I find it comical that some people refer to rugby-players as peanut-huggers. 194.221.133.226 (talk) 11:18, 5 September 2008 (UTC)

I was thinking more about the outer shell of the peanut, the part that looks sort of like dumbbells.--Honeymane_{Heghlu meH QaQ jajvam} 16:02, 5 September 2008 (UTC)

I think a mathematician would most likely call it "peanut shaped". Playing around with Greco-Roman roots I came up with "arachiform", for which a Google search actually turns up a few uses alongside such terms as "obpyriform". But I can't deduce from those few references whether "arachiform" refers to the shape of a peanut shell or of the nut inside or neither. -- BenRG (talk) 18:44, 5 September 2008 (UTC)

September 4

Plot request

Can someone plot an excel line graph for me and send it to me by e-mail or attach a rapidshare link ? I am an absolute wally when it comes to computers so please help me. Here is the table of data. It is a distance-time graph. Here it is:
distance (km) time (min)

You'll need your own pencil, though.

0.2 0.5
0.2 1
1.2 3
1.2 3.5
2.5 5
2.5 5.5
4.4 7
7.3 11
7.3 11.5
8.3 13
9.2 13.5
9.5 16
Please send it to me at [email address redacted to prevent spam] or upload it and give me a link. Thank you in advance.

Saintrain (talk) 20:52, 4 September 2008 (UTC)

You would be far better off learning to use Excel (or some other spreadsheet program). There are plenty of courses and online tutorials out there. We're not going to do it for you, that's not the purpose of this desk. We're here to help you learn and doing your work for you won't help that at all. --Tango (talk) 22:05, 4 September 2008 (UTC)

Calculator for student in college

Hello, I need to buy a graphing calculator for a student in college. I understand he is using a TI-89 (not titanium) now. He is a Math major and will most likely go to do graduate study in Math. What graphing calculator should I get for him? The TI-83 plus is significantly cheaper than a TI-89 Titanium (and there is a newer model already). However, TI-89 has CAS which earlier models don't. Is the TI-89 accepted in major tests like the GRE (general, Physics, Math, Chemistry) and so on?

Do you think the additional cost of the TI-89 is justified? How about a TI-89 Titanium? I also wonder if he is going to end up doing most of his work on a notebook computer or something. Thanks a lot. You guys are awesome! Kushal (talk) 23:18, 4 September 2008 (UTC)

I'm studying maths at Uni and have never needed a graphing calculator. They are banned from all exams offered by my department (few exams allow a calculator at all and those that do only allow a basic scientific calculator) and outside exams a computer is usually much better. Are you sure he really needs it? If it's for a particular course, whoever is taking the course will be able to recommend one, or at least give you a list of features he'll need. --Tango (talk) 00:20, 5 September 2008 (UTC)

He is taking a bunch of math classes with different professors. I don't want to overkill (or get a calculator so sophisticated that he cannot use in tests) but I want to buy him a decent graphing calculator so that it does not become worthless in his advanced graduate work. I am in the US, if it helps any. Kushal (talk) 00:41, 5 September 2008 (UTC)

He'll need to find out what the rules are if he wants to use it in exams. What area of Maths does he expect to do graduate study in? Unless its stats, I can't see him needing a graphics calculator for that any more than he needs one for undergrad work, and even then it's unlikely. --Tango (talk) 00:50, 5 September 2008 (UTC)

I don't know if this will help, but I'm studying Maths + Physics at a Uni in the UK. I bought a graphical calculator when I started at College (which is 16-18 here) and found it very useful, I was also allowed to use it in all of my exams. At university, I have very rarely had any use for it, and I am not allowed to use it in any exams (the university has a ban on some of its features, such as being able to store text). Another thing to consider is that his university might well have some CAS software like Matlab or Maple on its computers, which can do anything a graphing calculator can, plus much more (and a lot faster).84.12.252.210 (talk) 10:31, 5 September 2008 (UTC)

Yes, 84, we do have Maple in all departmentally owned computers. He could get Maple for his Macbook too. However, I am not sure any teacher in the department would allow using a MacBook in finals. This brings me to another question. Is the USB thingy for the titanium even compatible with macs? We have Intel Macbook with Tiger on it. Thanks. Kushal (talk) 12:32, 5 September 2008 (UTC)

I am a graduate student in math at Nebraska, and I use my TI-89 all the time for various things. On the other hand, in "advanced graduate work" any calculator is fairly useless, since most advanced math classes focus much more on logical reasoning and proof-writing rather than numerical calculation. At this point in my studies an advanced graphing calculator with a CAS like the TI-89 is mostly just a convenient luxury, but since I use it primarily for its CAS capabilities it's much more useful to me than a TI-83 or TI-84. —Bkell (talk) 10:47, 5 September 2008 (UTC)

Bkell, do you ever use custom apps or use your TI-89 with a computer? How useful has the USB thingy been to you? Kushal (talk) 12:32, 5 September 2008 (UTC)

September 5

How many different song variations are there?

It's probably an astronomical number, but the question came to me as I was reading about how one star supposedly was "inspired by" another star to write a similar song and successfully was sued. (It was the one with My Sweet Lord by George Harrison, and He's So Fine)

My question - which is why it's in the math section - is how many possible variations are there on a song? If 10,000 performers/bands each wrote, say, 100 songs a year, thus making a million songs a year, how long before they ran out of variations that were suitably different from each other, so no one performer could say, "Well, that sounds almost exactly like my song." Note that I'm not saying "the exacty same" - obviously, there are subtle differences in songs, but yet "My Sweet Lord" and "He's So Fine" were seen by a court to be similar enough.

I'm just amazed at how people on Name That Tune can guess a song after one note, or even seven; I'm part deaf, but even so, I'm amazed anormal hearing person can tell the difference between songs that seem to start so similarly.Somebody or his brother (talk) 00:22, 5 September 2008 (UTC)

There are enormous numbers of possibilities, the vast majority of which, however, will sound absolutely terrible. Calculating the total number of songs that anyone is likely to enjoy listening too is probably extremely difficult due to problems defining what people like. --Tango (talk) 00:59, 5 September 2008 (UTC)

Quite true. If the OP wants an idea of the magnitude, let's assume that there are 88 notes (the number of keys on a piano), that only a single note is played at any given time, that every note is held for the same amount of time, that there are no rests, and that the song is exactly 100 notes long. Given these restrictions, more "songs" can be composed than there are atoms in the known universe. Wikiant (talk) 01:36, 5 September 2008 (UTC)

There are more "songs" than the number of atoms in the observable universe squared. --Tango (talk) 01:47, 5 September 2008 (UTC)

Awww, but what fraction of those songs seems similar? Let's be more concrete. Lets songs be defined by sequences of notes (a_i) and (b_i), and define two songs as "similar" if there exists p,q,r such that (a_p,...,a_p+9) = (b_q + r,...,b_q+9 + r). In other words, they are similar if the same pattern of 10 notes occur in both songs modulo a change in pitch. Now for each real song there would be quite large space of disallowed similar songs. I'll leave estimating that number to someone with more free time ;-). Dragons flight (talk) 01:59, 5 September 2008 (UTC)

My extremely rough estimation (so rough I daren't share the details!) puts it somewhere in the trillions, at least. --Tango (talk) 02:17, 5 September 2008 (UTC)

Assume that a song can be recorded on a CD containing N bits. The total number of possible songs cannot exceed 2^N. A lower bound is obtained by using the observation that skilled people can identify a song after hearing M≈7 notes. Let A≈24 be the number of different pitches and B≈5 the number of different durations of a single note. Then the number of different songs are ≤(AB)^M≈120⁷=358318080000000. Bo Jacoby (talk) 07:23, 5 September 2008 (UTC).

I believe that part of what makes a song easily recognizable after just a few notes is its general "sound" (instrumentation, accompanying chords, tempo, echoes or lack of them and so on). So even songs that are "formally" very similar (say, sharing a subsequence of notes in their main melody) can be easily told apart. (On the other hand, they are not different in the sense of the OP.) If we could strip a song of all these factors, probably more notes would be necessary to recognize them. Goochelaar (talk) 11:28, 5 September 2008 (UTC)

You might want to reduce the number of songs by taking conventions of western music into account. Much of western music is in four-four time and the range of notes maybe span two/three octaves, further if we restrict to songs in a major key, the notes will tend to comprise the root note, the 3rd and the 5th, which sound more harmonious. (This is due to fact that 2^4/12≈5/4, 2^7/12≈3/2 see Just intonation). So if we ignore all the fancy jazz stuff and stick to major keys in four four time we will get a much reduced but still large number. I've read somewhere that there is actually quite a small number of common baselines or grooves which tend to be more repetative.

Maybe the correct mathematical way to workout the chance of two songs sounding the same would be more a bassian approach. Sample songs in a given genera, rescale so they are all in the same key, find frequency of each note and do the sums. --Salix alba (talk) 11:30, 5 September 2008 (UTC)

Differential equation

Hello. I've done another exam question and, as usual, I would like you kind people to check it for me. Same old story, please tell me if I'm right but if I'm wrong, let me know but don't tell me how, when, where or why.

Find functions f, g and h such that the equation

${\frac {d^{2}y}{dx^{2}}}+f(x){\frac {dy}{dx}}+g(x)y=h(x)$

is satisfied by $y=x$, $y=1$, $y=x^{-1}$ for 0<x<1.

If f, g and h are the functions from above, what condition must the real numbers a, b and c satisfy in order that

$y=ax+b+{\frac {c}{x}}$

should be a solution of the above differential equation?

I have

$f(x)=-{\frac {2}{x(x-1)}}$

$g(x)=h(x)={\frac {2}{x(x-1)^{2}}}$

and the final condition is a+b+c=1. Thanks 92.3.59.243 (talk) 19:09, 5 September 2008 (UTC)

Correct. Algebraist 19:19, 5 September 2008 (UTC)

Cheers. Really appreciate it. 92.3.59.243 (talk) 19:21, 5 September 2008 (UTC)