Bass Serre Tree

Bass-Serre trees are a construction from the mathematical branch of group theory with which group effects of amalgamated products or, more generally, fundamental groups of graphs of groups on trees can be constructed.

They are named after Hyman Bass and Jean-Pierre Serre .

definition

Let it be a graph of groups and its fundamental group . The corresponding Bass Serre tree is constructed as follows: ${\displaystyle (E,K,\left\{G_{e}\right\}_{e\in E},\left\{G_{k}\right\}_{k\in K},\left\{\alpha _{k,i}\colon G_{k}\to G_{e_{i}}\right\}_{k=(e_{0},e_{1})\in K,i=0,1})}$ ${\displaystyle G}$ ${\displaystyle T}$

• the corners are ${\displaystyle \bigsqcup _{e\in E}G/G_{e}}$
• the edges are ${\displaystyle \bigsqcup _{k\in K}G/G_{k}}$
• the edge has the corners and , for ${\displaystyle \left[g\right]\in G/G_{k}}$ ${\displaystyle \left[g\right]\in G/G_{e_{0}}}$ ${\displaystyle \left[gk\right]\in G/G_{e_{1}}}$ ${\displaystyle k=(e_{0},e_{1})\in K}$

The group acts on through left multiplications on and . ${\displaystyle G}$ ${\displaystyle T}$ ${\displaystyle G/G_{e}}$ ${\displaystyle G/G_{k}}$

${\displaystyle T}$ is a tree.

Structure set

Let it be a graph of groups and its Bass-Serre tree. Then the stabilizers of corners or edges are isomorphic to or for or and the quotient is the graph underlying the graph of groups . ${\displaystyle (E,K,\left\{G_{e}\right\}_{e\in E},\left\{G_{k}\right\}_{k\in K},\left\{\alpha _{k,i}\colon G_{k}\to G_{e_{i}}\right\}_{k=(e_{0},e_{1})\in K,i=0,1})}$ ${\displaystyle T}$ ${\displaystyle {\tilde {e}}}$ ${\displaystyle {\tilde {k}}}$ ${\displaystyle G_{e}}$ ${\displaystyle G_{k}}$ ${\displaystyle e=\left[{\tilde {e}}\right]}$ ${\displaystyle k=\left[{\tilde {k}}\right]}$ ${\displaystyle G\backslash T}$ ${\displaystyle (E,K)}$

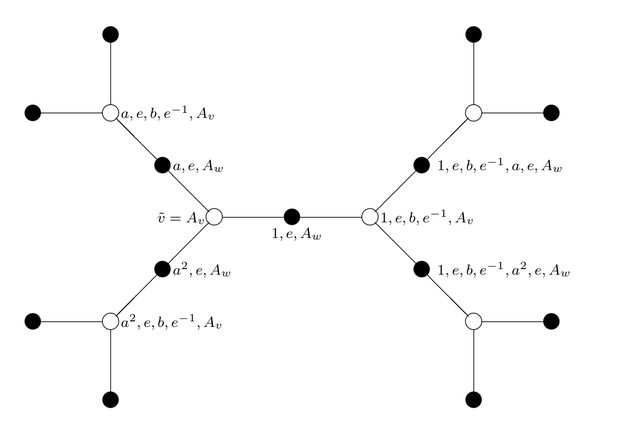
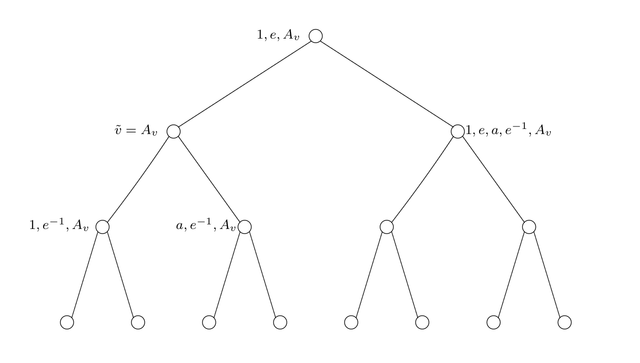
Examples

The following two graphs are the Bass-Serre trees of a free product and an HNN extension, respectively .

• Free Product Bass Serre Tree : ${\displaystyle \mathbb {Z} /2\mathbb {Z} *\mathbb {Z} /3\mathbb {Z} \simeq PSL(2,\mathbb {Z} )}$

• Bass Serre Tree of the Baumslag Solitar Group : ${\displaystyle BS(1,2)=\langle a,t\colon tat^{-1}=a^{2}\rangle }$

literature

Jean-Pierre Serre : Trees. Translated from the French original by John Stillwell. Corrected 2nd printing of the 1980 English translation. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. ISBN 3-540-44237-5

Web links

Richard Weidmann: Bass-Serre theory ( Memento from February 19, 2015 in the Internet Archive )

Individual evidence

1. ↑ Serre, op.cit., Theorem 12 in Chapter I.
2. ↑ Weidmann, op.cit., Chapter 5