Acceleration pole

Rigid body (yellow) with reference point s, acceleration pole p and accelerations (red)

The acceleration pole (symbol P) in a plane rigid body movement is the point in the plane at which the acceleration of a particle of the rigid body located there disappears. The acceleration pole lies with a movement in the xy-plane and rotation around the z-axis in the point (p _x , p _y ) with

${\displaystyle p_{x}=s_{x}+{\dfrac {\omega ^{2}{\ddot {s}}_{x}-{\dot {\omega }}{\ddot {s}}_{y}}{\omega ^{4}+{\dot {\omega }}^{2}}}\,,\quad p_{y}=s_{y}+{\dfrac {\omega ^{2}{\ddot {s}}_{y}+{\dot {\omega }}{\ddot {s}}_{x}}{\omega ^{4}+{\dot {\omega }}^{2}}}}$

The indices x and y refer to the spatial direction, s is the reference point around which the rigid body rotates, the acceleration of the reference point and the rotational speed and acceleration of the rigid body. ${\displaystyle {\ddot {s}}}$ ${\displaystyle \{\omega ,{\dot {\omega }}\}}$

Let the “pole distance” be the distance r of a particle at point z from the acceleration pole p (see picture). Then:

1. If the reference point is not accelerated, the acceleration pole is in the reference point.
2. The acceleration of the particle increases linearly with its pole distance.
3. When the rigid body rotates, all particles are accelerated in the direction of the acceleration pole, transversely only in the case of an angular acceleration of the rigid body.
4. The angle β between the direction of acceleration of the particle and the direction to the acceleration pole is the same for all particles in the rigid body and is at most 90 °. The particles are never driven radially away from the acceleration pole.
5. The acceleration of a particle in the direction of the acceleration pole increases proportionally to its pole spacing and the square of the angular velocity.
6. The acceleration of a particle 90 ° counterclockwise across the direction from the acceleration pole to the particle increases proportionally to its pole spacing and to the angular acceleration of the rigid body.

The position of the acceleration pole is interesting in the kinematics of vehicles, transmission technology and robotics.

Acceleration pole in the complex number plane

Latch level (yellow) with latching coordinates (black) and aisle level (sky blue) with aisle coordinates (blue)

The acceleration pole is only considered for plane movements and therefore the rigid body movement can be modeled as a movement of the complex plane of numbers. The fixed image space is the rest plane , which represents the space of our perception and which contains the rest coordinate system. The moving archetype space is the corridor level , which contains the rigid body resting in the corridor level and the corridor coordinate system. All particles of the rigid body move with the corridor. Based on the Eulerian and Lagrangian points of view , the coordinates in the rest plane are designated as spatial and with lower case letters and the coordinates in the corridor plane as material and with upper case letters, see picture.

Each point in the complex number plane corresponds to a complex number. The translation of a point is modeled with the addition of another number and the rotation around the origin with the product with the complex number , where the angle of rotation, e is Euler's number and i is the imaginary unit . ${\displaystyle e^{\mathrm {i} \phi }}$ ${\displaystyle \phi }$

The current location z, the speed and acceleration of a certain particle Z of the rigid body in the aisle level can then be increased in the locking level ${\displaystyle {\dot {z}}}$ ${\displaystyle {\ddot {z}}}$

${\displaystyle \chi (Z,t)=s+e^{\mathrm {i} \phi }Z=z\quad \rightarrow \quad {\dot {z}}={\dot {s}}+\mathrm {i} \omega e^{\mathrm {i} \phi }Z\quad \rightarrow \quad {\ddot {z}}={\ddot {s}}+\mathrm {i} {\dot {\omega }}e^{\mathrm {i} \phi }Z-\omega ^{2}e^{\mathrm {i} \phi }Z={\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z-s)}$

be calculated because according to the first relationship is . The point s denotes the reference point around which the corridor plane rotates with the rigid body and in which the origin of the corridor coordinate system lies. The rotational speed and acceleration results from the time derivatives of the rotation angle: . The acceleration pole p is now the place where it vanishes: ${\displaystyle e^{\mathrm {i} \phi }Z=z-s}$ ${\displaystyle \omega ={\dot {\phi }},\,{\dot {\omega }}={\ddot {\phi }}}$ ${\displaystyle {\ddot {p}}}$

${\displaystyle {\ddot {p}}={\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(p-s)=0\quad \rightarrow \quad {\begin{cases}{\ddot {s}}=(\mathrm {i} {\dot {\omega }}-\omega ^{2})(s-p)\\p=s+{\dfrac {\omega ^{2}+\mathrm {i} {\dot {\omega }}}{\omega ^{4}+{\dot {\omega }}^{2}}}{\ddot {s}}\end{cases}}}$

The real and imaginary parts of the acceleration pole p were given at the beginning. If the reference point is not driven, the acceleration pole is in the reference point. The acceleration at any place is

${\displaystyle {\ddot {z}}={\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z\underbrace {-p+p} _{=0}-s)=\underbrace {{\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(p-s)} _{={\ddot {p}}=0}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z-p)=\left(e^{\mathrm {i} {\frac {\pi }{2}}}{\dot {\omega }}-\omega ^{2}\right)(z-p)}$

The acceleration for all particles in the rigid body increases linearly with -fold the distance to the acceleration pole and closes the angle with the connection to the acceleration pole ${\displaystyle |\mathrm {i} {\dot {\omega }}-\omega ^{2}|={\sqrt {\omega ^{4}+{\dot {\omega }}^{2}}}}$

${\displaystyle \beta =\arg(\mathrm {i} {\dot {\omega }}-\omega ^{2})=-\arctan \left({\frac {\dot {\omega }}{\omega ^{2}}}\right)}$

a. The angle β always rotates in the opposite direction to the angular acceleration.

example

Accelerated wheel rolling to the right (black) with moving acceleration pole (red)

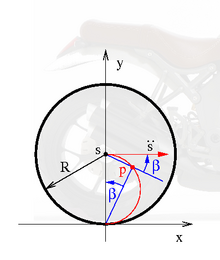
The rear wheel with radius R of an accelerating motorcycle is considered. The movement takes place in the complex xy plane parallel to the x axis in the positive x direction. The point of contact of the wheel is the origin at the beginning, so that the rear axle is initially at point s = x + iy = i R. The motorcycle starts moving with constant positive acceleration a in the direction of the positive x-axis. Then the acceleration of the motorcycle is equal to the acceleration of the wheel center, which provides the reference point:

${\displaystyle a={\ddot {s}}={\textsf {const.}}\,.}$

If the rear wheel rolls without slipping, s _y = R = const. and

${\displaystyle {\begin{array}{rcl}s_{x}&=&-R\phi \;\rightarrow {\dot {s}}_{x}=-R{\dot {\phi }}=-R\omega \;\rightarrow {\ddot {s}}_{x}=-R{\dot {\omega }}=a\\\rightarrow {\dot {\omega }}&=&-{\frac {a}{R}}\;\rightarrow \omega =-{\frac {at}{R}}\,,\;\rightarrow \phi =-{\frac {at^{2}}{2R}}\,.\end{array}}}$

because the rear wheel rotates clockwise with negative rotational speed around the z-axis. The acceleration pole is thus calculated

${\displaystyle {\begin{array}{rcl}p_{x}=s_{x}+{\dfrac {\omega ^{2}{\ddot {s}}_{x}-{\dot {\omega }}{\ddot {s}}_{y}}{\omega ^{4}+{\dot {\omega }}^{2}}}&=&s_{x}+{\dfrac {{\frac {a^{2}t^{2}}{R^{2}}}a}{{\frac {a^{4}t^{4}}{R^{4}}}+{\frac {a^{2}}{R^{2}}}}}=s_{x}+{\dfrac {R^{2}at^{2}}{a^{2}t^{4}+R^{2}}}\geq s_{x}\\p_{y}=s_{y}+{\dfrac {\omega ^{2}{\ddot {s}}_{y}+{\dot {\omega }}{\ddot {s}}_{x}}{\omega ^{4}+{\dot {\omega }}^{2}}}&=&R+{\dfrac {-{\frac {a}{R}}a}{{\frac {a^{4}t^{4}}{R^{4}}}+{\frac {a^{2}}{R^{2}}}}}=R-{\dfrac {R^{3}}{a^{2}t^{4}+R^{2}}}\geq 0\\\rightarrow \left(p_{y}-{\dfrac {R}{2}}\right)^{2}+(p_{x}-s_{x})^{2}&=&{\dfrac {R^{2}}{4}}\end{array}}}$

As the picture suggests, the acceleration pole lies on a circle with half the tire radius between the contact point and the wheel center.

The ratio of the horizontal distance of the acceleration pole to its height above the "road" is

${\displaystyle {\begin{array}{rcl}{\dfrac {p_{x}-s_{x}}{p_{y}}}&=&{\dfrac {\dfrac {R^{2}at^{2}}{a^{2}t^{4}+R^{2}}}{\dfrac {R(a^{2}t^{4}+R^{2})-R^{3}}{a^{2}t^{4}+R^{2}}}}={\dfrac {R^{2}at^{2}}{Ra^{2}t^{4}}}={\dfrac {R}{at^{2}}}=-{\dfrac {-{\frac {a}{R}}}{\left({\frac {at}{R}}\right)^{2}}}=-{\dfrac {\dot {\omega }}{\omega ^{2}}}=\tan \;\beta \,.\end{array}}}$

The angle β measures counterclockwise and is positive. Initially, at time t = 0, β = 90 °, because the wheel is not yet turning but the angular acceleration is not equal to zero. The point of contact of the wheel is then the acceleration pole and the acceleration is like the speed field of a uniformly rolling wheel, see momentary pole . With increasing speed, the acceleration pole moves on the semicircle towards the wheel center. The angle between the acceleration pole, the contact point and the y-axis is the angle β, which tends to zero over time because the angular acceleration is constant, but the angular velocity continues to increase. Geometric and kinematic reasons mean that the wheel center is always driven precisely in the x direction.

If no further acceleration is achieved after reaching the target speed, then p = s: The acceleration pole jumps to the wheel center and all particles of the wheel are pulled towards the wheel center and acceleration pole with the centripetal acceleration known from the uniform rotation . ${\displaystyle {\ddot {s}}=0}$

See also

• Traveling pole chain
• Rastpolbahn
• Gangpolbahn
• Pole plan
• Euclidean transformation
• Velocity gradient # rigid body motion
• Orthogonal tensor # Rigid body motions

literature

• H. Klepp: Technical Mechanics, Kinematics and Kinetics 1 . Pro Business, 2013, ISBN 978-3-86386-476-7 .
• G. Bär: Level kinematics . Script for the lecture. Institute for Geometry, TU Dresden ( tu-dresden.de [PDF; accessed on April 1, 2015] Contains further literature recommendations ).