Momentary pole

Linkage : The current motion state of the coupling (blue), can be applied to rotation about the instantaneous center P reduziereren. The velocity vectors v at points A, B and C are perpendicular to the rays from P to the points, which uniquely determines P. The speed is proportional to the distance to P.

In the case of a plane movement of a rigid body, the momentary center is that point in space around which the body can be viewed and treated as only rotating at the moment (time, infinitesimal). The velocity at the instantaneous pole is zero at the moment in question or it would be if the rigid body expanded to the instantaneous pole, see picture.

If the instantaneous poles occurring during a movement are marked, the latching pole path is created in the fixed reference system and the gang pole path in the reference system of the moving body . The gang pole track rolls smoothly on the locking pole track.

The momentary pole is an abstraction used in kinematics that is used in transmission technology , robotics and the design of wheel guides in automobiles .

Historical

Michel Chasles formulated the sentence (as he himself suspected, for the first time) in 1830:

“Quand on a dans l'espace un corps solid libre, si on lui fait éprouver un déplacement fini quelconque, il existera toujours dans ce corps une certaine droite indéfinie, qui, aprés le déplacement, se retrouvera au même lieu qu'auparavant. »

"If you have a free rigid body in space and if you move it at will, but finally, there will always be a certain indeterminate straight line in this body, which, after the displacement, will find itself again in the same place as before."

This description applies to the instantaneous pole of an infinitesimal movement. Giulio Mozzi, however, was already concerned with rigid body movements in 1763.

Construction of the momentary pole

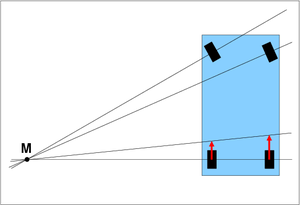
If, in a rigid body rolling on four wheels, all wheel axles meet at the momentary pole M , the body can move in the plane without the wheels sliding.
The speed vectors of the rear axle wheels are shown as red arrows.

With a rotation, the speed of each point is perpendicular to the connection of this point with the axis of rotation (instantaneous pole). The momentary pole can be determined if the speeds of two points are known.

If both speeds are equal in magnitude and direction, it is a pure translation, and the instantaneous pole is at infinity in the direction of the perpendicular to the two speed vectors.
If the directions of speed of both points are not parallel, as in the case of the wheel centers of the two front wheels in the picture, then the intersection of the perpendicular to the speed vectors in the two points is the instantaneous pole.
If the speeds of both points are parallel, but - as with the rear wheels in the picture - have different magnitudes, the instantaneous pole is the intersection of the line connecting the two points and the line connecting the peaks of both speed vectors.

As an alternative to this construction, the position of the instantaneous pole can also be calculated, see detent pole and gear pole path .

definition

Every rigid body movement can be broken down into a translation and a rotation, which Michel Chasles also noticed. The translation is given with the time-dependent reference point for which every moving (or also resting) point and also the center of gravity of the rigid body is suitable. The rotation takes place around an axis of rotation which points in the direction of the rotation speed vector , the Frobenius norm of which indicates the rotation speed. The speed of a particle in one place is with a rigid body movement ${\ displaystyle {\ vec {s}} (t)}$ ${\ displaystyle {\ vec {\ omega}} (t)}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle {\ vec {v}} ({\ vec {x}}, t) = {\ dot {\ vec {s}}} (t) + {\ vec {\ omega}} (t) \ times {\ bigl (} {\ vec {x}} - {\ vec {s}} (t) {\ bigr)}}

given. The arithmetic symbol "×" forms the cross product and is the speed of the reference point. The momentary center is now a point in space in which the velocity field is currently represented as a pure rotation: ${\ displaystyle {\ dot {\ vec {s}}} (t)}$ ${\ displaystyle {\ vec {m}} (t)}$

${\ displaystyle {\ vec {v}} ({\ vec {x}}, t) = {\ dot {\ vec {s}}} (t) + {\ vec {\ omega}} (t) \ times {\ bigl (} {\ vec {x}} - {\ vec {s}} (t) {\ bigr)} {\ stackrel {\ displaystyle!} {=}} {\ vec {\ omega}} (t ) \ times {\ bigl (} {\ vec {x}} - {\ vec {m}} (t) {\ bigr)} \ ,.}$		(Definition)

With this point, all points are on the straight line with instantaneous poles. Scalar multiplication of the speed by the rotational speed vector disclosed ${\ displaystyle {\ vec {m}} + \ lambda {\ vec {\ omega}}}$ ${\ displaystyle \ lambda \ in \ mathbb {R}}$

{\ displaystyle {\ vec {v}} ({\ vec {x}}, t) \ cdot {\ vec {\ omega}} (t) = {\ dot {\ vec {s}}} (t) \ cdot {\ vec {\ omega}} (t) = {\ vec {\ omega}} (t) \ cdot \ left [{\ vec {\ omega}} (t) \ times {\ bigl (} {\ vec {x}} - {\ vec {m}} (t) {\ bigr)} \ right] = 0 \ ,,}

d. H. the speed of the reference point must be perpendicular to the axis of rotation so that there can be a momentary pole. At the moment the movement must therefore - as mentioned at the beginning - be a plane.

If the rotational speed disappears, then the speed is not dependent on the location and is therefore uniform. The equation of definition ${\ displaystyle {\ vec {v}} ({\ vec {x}}, t) = {\ dot {\ vec {s}}} (t)}$

{\ displaystyle {\ vec {v}} ({\ vec {x}}, t) = {\ dot {\ vec {s}}} (t) {\ stackrel {\ displaystyle!} {=}} {\ vec {0}} \ times {\ bigl (} {\ vec {x}} - {\ vec {m}} (t) {\ bigr)} = {\ vec {0}}}

then no longer contains any definition and the momentary pole is therefore not defined. Occasionally, the instantaneous center of gravity is shifted to an infinitely distant point on the perpendicular to the direction of motion in the case of a uniform motion, which is useful with finite rigid bodies.

Paradox of the moving momentary pole

The instantaneous pole depends on time and can therefore move through space. On the other hand, the speed at the momentary pole disappears at any time:

{\ displaystyle {\ vec {v}} ({\ vec {m}} (t), t) = {\ vec {\ omega}} (t) \ times {\ bigl (} {\ vec {m}} (t) - {\ vec {m}} (t) {\ bigr)} = {\ vec {0}} \ ,,}

which is also eponymous for the momentary pole. But how can something move that stands still?

One cause of this apparent contradiction lies in the identification of a particle with the point in space at which it is located. The speed field formulated with Euler's point of view indicates the speed of a particle located in the location and the speed of the particle standing still at the momentary pole is correspondingly . The momentary pole is not this particle, but only the geometric location where it is located. Just like the reference point or the axis of rotation, the instantaneous center of gravity is a parameter of the movement that represents a geometric object . The momentary pole points like a pointer to a point in space and in this point in space, if something is located there, there is a standstill. This point in space does not necessarily have to lie in the rigid body. The momentary pole is not bound to particles and can roam fluently through the plane as long as the particles only stop momentarily in the momentary pole (if a particle stops, then the momentary pole is there as long as it is). ${\ displaystyle {\ vec {v}} ({\ vec {x}}, t)}$ ${\ displaystyle {\ vec {x}}}$ ${\ displaystyle {\ vec {v}} ({\ vec {m}}, t)}$

A second cause of the paradox lies in the different modes of movement of the particles and the momentary pole. In classical mechanics , space is absolute, unchangeable and unaffected by physical processes and accordingly points in space cannot move in the mechanical sense, but only in the mathematical sense . So while the particles move in the mechanical sense, the momentary pole moves in the mathematical sense. The momentary pole is a function of time that outputs a point in space. If the momentary pole does not stand still, then at any point in time - if at all - other particles are at the place of the momentary pole. From a mechanical point of view, a sequence of instantaneous poles in a movement is an alternative to the paradoxical idea of a moving instantaneous pole.

All particles of the rigid body, which ever come to a standstill in a momentary pole, lie on the gang pole orbit while the rest pole orbit is the set of all spatial points that are at some point momentary pole. The gang pole track rolls smoothly on the locking pole track because the pole change speeds on the locking pole track and the gang pole track are the same. At the momentary pole, the points in space alternate just as quickly as the particles of the rigid body (provided the momentary pole is in the rigid body).

Example: rolling wheel

Example wheel: Momentary pole (M here M = A) on a wheel that is mounted on a vehicle

The wheel on a vehicle shown in the picture has several properties from the point of view of kinematics if you look at it along the dashed line through the center of rotation (Z) and the contact point (A):

Since it is attached to the vehicle, it takes part in its translational movement. This proportion is shown by the speed arrows (T) along line (L).

An observer in the center (Z) sees that the wheel (in contrast to the vehicle) also rotates around this center (Z). This proportion is represented by the arrows (R) of the tangential velocities along the line (L).

As long as the wheel is rolling, it has speed 0 at the point of contact (A), because the road is stationary and the wheel does not slip over the road at this point and in this idealized view does not slip either.

The superposition of the speeds (R) and (T) as well as the condition that the point on the wheel that is the point of contact (A) on the stationary road itself must also be, makes the point of contact (A) at the same time the point of contact (M) the wheel movement.

The illustration on the right shows how the instantaneous speed can be determined with the help of the instantaneous pole (M) at four selected points A – D: It is the product of the angular velocity ω around the instantaneous pole (M, the same angular velocity as around Z) and the Distance of the respective point (in the example A ... D) from the instantaneous pole (M). For example, if you look for the point on the wheel that is furthest away from the instantaneous pole, you have found the point with the highest speed.

The Rastpolbahn is the road in this example, because from the point of view of an observer on the road, all momentary poles are on the road. From the perspective of an observer on the wheel, the gang pole track is the circumference.

The momentary pole should now also be calculated. A Cartesian coordinate system with mutually perpendicular x, y and z directions and the associated standard basis is given . The x-axis represents the road on which the wheel begins to roll in the origin of the xy-plane at time t = 0. The wheel has the radius R and a uniform rotational speed ω = -Ω <0 around the z-axis and thus rolls on the x-axis in the positive x-direction. The center point of the axis is then at the height R above the x-axis and should move parallel to the x-axis. From the point of view of the center of the axis, a particle P located on the wheel circumference has the speed and the opposite point of the axis center has the same speed from the point of view of this particle P. The contact point A of the wheel on the x-axis is such a particle. The center of the axis and its speed are accordingly with ${\ displaystyle {\ vec {e}} _ {x, y, z}}$ ${\ displaystyle \ Omega \, R}$ ${\ displaystyle {\ vec {s}} (t)}$

{\ displaystyle {\ vec {s}} (t = 0) = R {\ vec {e}} _ {y} \; \ wedge \; {\ dot {\ vec {s}}} (t) = \ Omega R {\ vec {e}} _ {x} \ quad \ leftrightarrow \ quad {\ vec {s}} (t) = \ Omega Rt {\ vec {e}} _ {x} + R {\ vec { e}} _ {y}}

given. The velocity field is therefore:

{\ displaystyle {\ begin {array} {rcl} {\ vec {v}} (x, y, t) & = & \ Omega R {\ vec {e}} _ {x} - \ Omega {\ vec { e}} _ {z} \ times (x {\ vec {e}} _ {x} + y {\ vec {e}} _ {y} - \ Omega Rt {\ vec {e}} _ {x} -R {\ vec {e}} _ {y}) = - \ Omega {\ vec {e}} _ {z} \ times (R {\ vec {e}} _ {y} + x {\ vec { e}} _ {x} + y {\ vec {e}} _ {y} - \ Omega Rt {\ vec {e}} _ {x} -R {\ vec {e}} _ {y}) \ \ & = & - \ Omega {\ vec {e}} _ {z} \ times (x {\ vec {e}} _ {x} + y {\ vec {e}} _ {y} - \ underbrace { \ Omega Rt {\ vec {e}} _ {x}} _ {= {\ vec {m}} (t)}) \ end {array}}}

from which it follows immediately . This also results from the formula given in the article on the Rastpolbahn: ${\ displaystyle {\ vec {m}} (t) = \ Omega Rt {\ vec {e}} _ {x}}$

{\ displaystyle {\ begin {array} {rcl} x_ {M} & = & x_ {S} - {\ frac {v_ {Sy}} {\ omega}} = \ Omega Rt - {\ frac {0} {- \ Omega}} = \ Omega Rt \\ y_ {M} & = & y_ {S} + {\ frac {v_ {Sx}} {\ omega}} = R + {\ frac {\ Omega R} {- \ Omega} } = 0 \ end {array}}}

Individual evidence

↑ ^a ^b M. Chasles: Note on les propriétés générales du système de deux corps semblables entr'eux . In: Bulletin des Sciences Mathématiques, Astronomiques, Physiques et Chemiques . tape 14 , 1830, p. 323–324 (French, limited preview in Google Book search).
↑ Giulio Mozzi: Discorso matematico sopra il rotamento momentaneo dei corpi . Stamperia di Donato Campo, Napoli 1763 (Italian, archive.org [accessed April 1, 2015]).

literature

M. Husty: Kinematics and Robotics . Springer, 2012, ISBN 978-3-642-63822-0 .

K. Luck, K.-H. Modler: Gear Technology: Analysis Synthesis Optimization . Springer, 1990, ISBN 978-3-211-82147-3 .

Ulrich Gabbert , Ingo Raecke: Technical mechanics for industrial engineers . HANSER_VERLAG, 2007 ISBN 3-446-41409-6

G. Bär: Level kinematics . Script for the lecture. Institute for Geometry, TU Dresden ( tu-dresden.de [PDF; accessed on April 1, 2015] Contains further literature recommendations ).

Rolf Mahnken: Textbook of Technical Mechanics . Basics and Applications. 2nd Edition. tape 1 : Rigid body statics. Springer Vieweg, Berlin, Heidelberg 2016, ISBN 978-3-662-52784-9 .

Web links

Momentanpol at a paddock (68.1 MB; .avi) , video of an animation by the Institute for Applied Mechanics, TU Munich

[chasles-1] M. Chasles: Note on les propriétés générales du système de deux corps semblables entr'eux . In: Bulletin des Sciences Mathématiques, Astronomiques, Physiques et Chemiques . tape 14 , 1830, p. 323–324 (French, limited preview in Google Book search).

[2] Giulio Mozzi: Discorso matematico sopra il rotamento momentaneo dei corpi . Stamperia di Donato Campo, Napoli 1763 (Italian, archive.org [accessed April 1, 2015]).