Rastpolbahn

Animated crank arm :
red: velocity vectors;
Yellow point: momentary pole ;
Blue: detent pole track of the middle bar;
Green: gang pole path of the middle rod

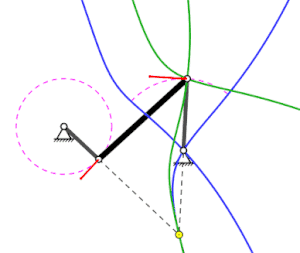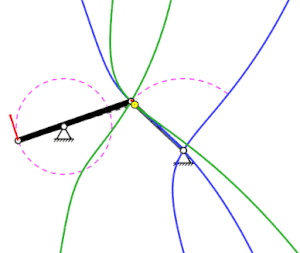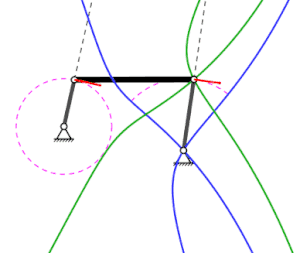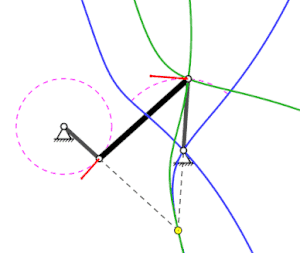
The Rastpolbahn ( English fixed centrode ) is the totality of all spatial points in the spatially fixed reference system that are ever the instantaneous pole in a rigid body movement . The instantaneous center of gravity is the point that is stationary during a rigid body movement. This only exists in the case of flat, not purely translational movements and therefore the latching pole track is a flat curve, see picture.

The following applies to the detent pole path when moving in the xy plane and rotating around the z axis:

${\displaystyle x_{M}=x_{A}-{\frac {v_{Ay}}{\omega }}}$

${\displaystyle y_{M}=y_{A}+{\frac {v_{Ax}}{\omega }}}$

The index “M” refers to the instantaneous pole, “A” to any point in the body, (x, y) are the coordinates in the plane, (v _x , v _y ) are the speeds in the x and y direction and ω is the angular velocity around the z-axis. If ω = 0, then there is a translation and the momentary pole and the point on the detent pole path assigned to it are not defined.

The Rastpolbahn is interesting in the kinematics of vehicles, gear technology, robotics and also prosthetics.

Rastpolbahn in three dimensions

A Cartesian coordinate system with mutually perpendicular x, y and z directions and the associated standard basis is given . The translation of the rigid body takes place parallel to the xy plane and the rotation around the z axis. The translation is given with a time-dependent reference point for which every moving (or also resting) point and also the center of gravity of the rigid body are suitable. The rotation takes place around the z-axis with the rotational speed ω. The speed of a particle in one place is with a rigid body movement ${\displaystyle {\vec {e}}_{x,y,z}}$ ${\displaystyle {\vec {s}}}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)+\omega (t){\vec {e}}_{z}\times {\bigl (}{\vec {x}}-{\vec {s}}(t){\bigr )}}$

given. The arithmetic symbol "×" forms the cross product and is the speed of the reference point. The momentary center is now a point in space around which the velocity field is currently represented as a pure rotation: ${\displaystyle {\dot {\vec {s}}}}$ ${\displaystyle {\vec {m}}(t)}$

${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)+\omega (t){\vec {e}}_{z}\times {\bigl (}{\vec {x}}-{\vec {s}}(t){\bigr )}{\stackrel {\displaystyle !}{=}}\omega (t){\vec {e}}_{z}\times {\bigl (}{\vec {x}}-{\vec {m}}(t){\bigr )}}$

With this point, all points on the straight line are also instantaneous poles, which is why the z component of the instantaneous pole is indefinite. Be the instantaneous, the same z component has as the reference point: . If the rotational speed disappears, then the speed is not dependent on the location and is therefore uniform. The equation of definition ${\displaystyle {\vec {m}}+\lambda {\vec {e}}_{z}}$ ${\displaystyle {\vec {m}}}$ ${\displaystyle {\vec {e}}_{z}\cdot ({\vec {m}}-{\vec {s}})=0}$ ${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)}$

${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)={\vec {0}}\times {\bigl (}{\vec {x}}-{\vec {m}}(t){\bigr )}={\vec {0}}}$

then no longer contains any definition and the momentary pole is therefore not defined. The following is assumed. ${\displaystyle \omega \neq 0}$

The cross product of the axis of rotation with the speed gives:

${\displaystyle {\vec {e}}_{z}\times {\vec {v}}({\vec {m}},t)={\vec {e}}_{z}\times {\dot {\vec {s}}}(t)+{\vec {e}}_{z}\times [\omega (t){\vec {e}}_{z}\times ({\vec {m}}(t)-{\vec {s}}(t))]={\vec {e}}_{z}\times {\dot {\vec {s}}}(t)-\omega (t)({\vec {m}}(t)-{\vec {s}}(t))={\vec {0}}}$

Because the rotational speed is not zero, the following can be resolved for the instantaneous pole:

${\displaystyle {\vec {m}}(t)={\vec {s}}(t)+{\dfrac {1}{\omega (t)}}{\vec {e}}_{z}\times {\dot {\vec {s}}}(t)\quad \rightarrow \quad {\vec {s}}(t)-{\vec {m}}(t)={\dfrac {1}{\omega (t)}}{\dot {\vec {s}}}(t)\times {\vec {e}}_{z}}$

The formula on the left presents the latching pole path parameterized with time t. As the formula on the right shows, the vectors form an orthogonal legal system . It is confirmed that the momentary center only depends on the parameters of the movement and not on the spatial coordinates and is therefore itself a location-independent movement parameter . Because any point can be chosen as a reference point, this formula applies generally, which is verified by substituting : ${\displaystyle {\vec {e}}_{z},\,{\vec {s}}-{\vec {m}},\,{\dot {\vec {s}}}}$ ${\displaystyle \{{\vec {s}}(t),{\dot {\vec {s}}}(t),\omega (t)\}}$ ${\displaystyle {\dot {\vec {s}}}(t)={\vec {v}}({\vec {x}},t)-\omega (t){\vec {e}}_{z}\times {\bigl (}{\vec {x}}-{\vec {s}}(t){\bigr )}}$

${\displaystyle {\vec {m}}(t)={\vec {x}}+{\dfrac {1}{\omega (t)}}{\vec {e}}_{z}\times {\vec {v}}({\vec {x}},t)\quad \rightarrow \quad {\vec {x}}-{\vec {m}}(t)={\dfrac {1}{\omega (t)}}{\vec {v}}({\vec {x}},t)\times {\vec {e}}_{z}}$

Instead of the reference point and its speed, this formula contains any point in space and the speed present in it. The xy components of this equation were given at the beginning. For each point in space, the axis of rotation , the distance vector to the instantaneous pole and the speed form an orthogonal right system. ${\displaystyle {\vec {e}}_{z}}$ ${\displaystyle {\vec {x}}-{\vec {m}}}$ ${\displaystyle {\vec {v}}}$

Rastpolbahn in the complex number plane

Latch level (yellow) with latching coordinates (black) and aisle level (sky blue) with aisle coordinates (blue)

The instantaneous center of gravity and the detent pole path are only defined in the case of plane movements and therefore the plane rigid body movement can be modeled as a movement of the complex plane of numbers. The fixed image space is the locking plane, which represents the space of our perception and which contains the locking coordinate system and the locking pole path. The moving archetype space is the corridor level, which contains the rigid body resting in it and the corridor coordinate system. All particles of the rigid body move synchronously with the aisle level. Based on the spatial Eulerian and the material Lagrangian point of view , the coordinates in the rest plane are designated as spatial and with lowercase letters and the coordinates in the corridor plane as material and with uppercase letters, see picture.

Each point in the complex number plane corresponds to a complex number. The translation of this point is modeled as the addition of another number and the rotation around the origin as a product with the complex number , with the angle of rotation , Euler's number e and the imaginary unit i. ${\displaystyle e^{\mathrm {i} \varphi }}$ ${\displaystyle \varphi }$

The motion function χ (Z, t) and the material velocity field of material points Z can then be called ${\displaystyle {\dot {\chi }}(Z,t)}$

${\displaystyle \chi (Z,t)=s(t)+e^{\mathrm {i} \varphi (t)}Z=z\quad \rightarrow \quad {\dot {\chi }}(Z,t)={\dot {s}}(t)+\mathrm {i} \omega (t)e^{\mathrm {i} \varphi (t)}Z}$

to be written. The point s (t) denotes a moving point of reference, in which the origin of the gear coordinate system, and the rotational speed ω is obtained from the time derivative of the angle of rotation: . Replacement of the material point by its spatial image z provides the spatial velocity field in the locking plane ${\displaystyle \omega ={\dot {\varphi }}}$ ${\displaystyle Z=e^{-\mathrm {i} \varphi (t)}(z-s(t))}$

${\displaystyle v(z,t):={\dot {s}}(t)+\mathrm {i} \omega (t)e^{\mathrm {i} \varphi (t)}e^{-\mathrm {i} \varphi (t)}(z-s(t))={\dot {s}}(t)+\mathrm {i} \omega (t)(z-s(t)).}$

At the momentary pole m (t) this speed disappears:

${\displaystyle v(m(t),t)={\dot {s}}(t)+\mathrm {i} \omega (t)(m(t)-s(t)){\stackrel {\displaystyle !}{=}}0\quad \rightarrow \quad m(t)=s(t)+{\frac {\mathrm {i} }{\omega (t)}}{\dot {s}}(t)}$

In the determining equation for the momentary pole m (t) can be inserted with the result: ${\displaystyle {\dot {s}}(t)=v(z,t)-\mathrm {i} \omega (t)(z-s(t))}$

${\displaystyle m(t)=z+{\frac {\mathrm {i} }{\omega (t)}}v(z,t)\quad \leftrightarrow \quad v(z,t)=e^{\mathrm {i} {\frac {\pi }{2}}}\omega (t)(z-m(t))}$

The formula on the left denotes the detent pole path in the detent plane, the real and imaginary parts of which are specified at the beginning. The formula on the right shows: The speed of a particle is ω times the distance from the instantaneous pole to the particle, rotated 90 ° counterclockwise.

example

Detent pole and gear pole path for a cross slide that revolves on a circular path and rotates in the opposite direction (animation 1.6 MB)

The latching pole path of the system given in the picture on the right is to be calculated. The cross slide has the length 2r and its center point moves with the angular velocity Ω on the circular path with the radius R around the origin. Then the midpoint of the cross slide is given by: ${\displaystyle {\vec {s}}(t)}$

${\displaystyle {\vec {s}}(t)=R\cos(\Omega t){\vec {e}}_{x}+R\sin(\Omega t){\vec {e}}_{y}}$

The cross slide rotates around its center point at an angular velocity ω = −Ω in the opposite direction. For a point on the cross slide at a distance r from the center point the position results:

${\displaystyle {\vec {x}}(r,t)=R\cos(\Omega t){\vec {e}}_{x}+R\sin(\Omega t){\vec {e}}_{y}+r\cos(-\Omega t){\vec {e}}_{x}+r\sin(-\Omega t){\vec {e}}_{y}=(R+r)\cos(\Omega t){\vec {e}}_{x}+(R-r)\sin(\Omega t){\vec {e}}_{y}}$

Deriving from time gives the speed:

${\displaystyle {\vec {v}}(r,t)=-\Omega (R+r)\sin(\Omega t){\vec {e}}_{x}+\Omega (R-r)\cos(\Omega t){\vec {e}}_{y}}$

The formulas given at the beginning provide the detent pole track:

${\displaystyle {\begin{array}{rcl}x_{M}&=&x_{A}-{\frac {v_{Ay}}{\omega }}=(R+r)\cos(\Omega t)-{\frac {\Omega (R-r)\cos(\Omega t)}{-\Omega }}=2R\cos(\Omega t)\\y_{M}&=&y_{A}+{\frac {v_{Ax}}{\omega }}=(R-r)\sin(\Omega t)+{\frac {-\Omega (R+r)\sin(\Omega t)}{-\Omega }}=2R\sin(\Omega t)\end{array}}}$

Regardless of the length of the cross slide, the circle with twice the radius of the circular path of the reference point is the latching pole path. In the picture above the cross slide is drawn in bold black and has the length r = R.

In the complex plane of numbers, the reference point is and the point on the cross slide running around the reference point is modeled as a particle Z rotating at the opposite angular velocity ω = −Ω: ${\displaystyle s=Re^{\mathrm {i} \Omega t}}$

${\displaystyle {\begin{array}{rcl}\chi (Z,t)&=&Re^{\mathrm {i} \Omega t}+e^{-\mathrm {i} \Omega t}Z=z\quad \rightarrow \quad Z=e^{\mathrm {i} \Omega t}(z-Re^{\mathrm {i} \Omega t})\\{\dot {\chi }}(Z,t)&=&\mathrm {i} \Omega Re^{\mathrm {i} \Omega t}-\mathrm {i} \Omega e^{-\mathrm {i} \Omega t}Z=\mathrm {i} \Omega Re^{\mathrm {i} \Omega t}-\mathrm {i} \Omega e^{-\mathrm {i} \Omega t}e^{\mathrm {i} \Omega t}(z-Re^{\mathrm {i} \Omega t})=:v(z,t)\\\rightarrow v(z,t)&=&\mathrm {i} \Omega (2Re^{\mathrm {i} \Omega t}-z)\,,\end{array}}}$

because the particle Z should rest in the aisle plane. The instantaneous pole is calculated from this spatial velocity field:

${\displaystyle {\begin{array}{rcl}v(m(t),t)&=&\mathrm {i} \Omega (2Re^{\mathrm {i} \Omega t}-m(t))=0\quad \rightarrow \quad m(t)=2Re^{\mathrm {i} \Omega t}\end{array}}}$

The formula for the detent pole track gives the same result:

${\displaystyle m(t)=z+{\frac {\mathrm {i} }{\omega (t)}}v(z,t)=z+{\frac {\mathrm {i} }{-\Omega }}\mathrm {i} \Omega (2Re^{\mathrm {i} \Omega t}-z)=2Re^{\mathrm {i} \Omega t}}$

Here, too, there is a circular path with a radius twice as large as the circular path of the reference point as a latching pole path.

See also

• Acceleration pole
• Traveling pole chain
• Pole plan
• Euclidean transformation
• Velocity gradient # rigid body motion
• Orthogonal tensor # Rigid body motions

literature

• M. Husty: Kinematics and Robotics . Springer, 2012, ISBN 978-3-642-63822-0 .
• K. Luck, K.-H. Modler: Transmission technology. Analysis synthesis optimization . Springer, 1990, ISBN 978-3-211-82147-3 .
• G. Bär: Level kinematics . Script for the lecture. Institute for Geometry, TU Dresden ( tu-dresden.de [PDF; accessed on April 1, 2015] Contains further literature recommendations ).

Web link

Commons : Rast- und Gangpolbahnen  - Collection of pictures, videos and audio files