Bialgebra

Bialgebra
touches the specialties
mathematics Abstract algebra Linear Algebra Commutative algebra
is a special case of
algebra Koalgebra
includes as special cases
Hopf algebra

A bialgebra has both the structure of a unitary, associative algebra and the dual structure of a koalgebra . The most important special case of bialgebras are Hopf algebras , to which the quantum groups also belong.

definition

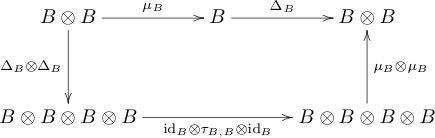
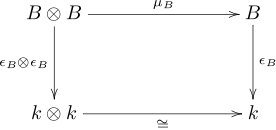
Be a field and be both unitary associative algebra over and koalgebra over . Denote the multiplication, the one (embedding the body in the algebra), the multiplication and the koeins. ${\displaystyle k}$ ${\displaystyle B}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle \mu _{B}}$ ${\displaystyle \eta _{B}}$ ${\displaystyle \Delta _{B}}$ ${\displaystyle \epsilon _{B}}$

${\displaystyle B}$is called bialgebra over if the following equivalent compatibility conditions are met. ${\displaystyle k}$

• The multiplication and the koeins are algebra homomorphisms. ${\displaystyle \Delta _{B}}$ ${\displaystyle \epsilon _{B}}$
• The multiplication and the one are koalgebra homomorphisms. ${\displaystyle \mu _{B}}$ ${\displaystyle \eta _{B}}$
• The following diagrams commute

Here is the "flip" mapping, i.e. the canonical isomorphism of the tensor products and applied to . ${\displaystyle \tau _{B,B}:=v\otimes w\mapsto w\otimes v}$ ${\displaystyle V\otimes W}$ ${\displaystyle W\otimes V}$ ${\displaystyle B\otimes B}$

The bialgebras, together with the maps, which are both algebra and koalgebra homomorphisms, form a category.

generalization

Algebras and coalgebras can be viewed in any monoidal category . For compatibility conditions, however, it is necessary that the tensor product of a (Ko) algebra is also a (Ko) algebra in a natural way, this requires the existence of a braid .

literature

• Christian Kassel: Quantum Groups (Graduate Texts in Mathematics) . Springer-Verlag, ISBN 0-387-94370-6