Cobordism

In mathematics , the concept of cobordism (also: bordism ) is particularly important in topology and its applications as well as in topological quantum field theory . It is considered to be the most “calculable” relation among manifolds that is geometrically interesting.

${\displaystyle W}$is a cobordism between and . ${\displaystyle M}$ ${\displaystyle N}$

René Thom (1954) is considered to be the creator of the cobordism theory , although some crucial ideas were anticipated by Lew Pontryagin (1950 and before).

definition

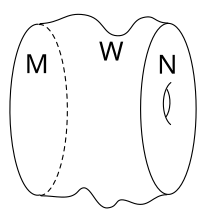
A cobordism between two manifolds and is a manifold for whose boundary holds ${\displaystyle M}$ ${\displaystyle N}$ ${\displaystyle W}$ ${\displaystyle \partial W}$

${\displaystyle \partial W=M\cup N}$.

The circle is oriented cobordant to the union of two circles.

${\displaystyle M}$and are then referred to as unoriented cobordant . ${\displaystyle N}$

However, the oriented cobordism is more often used. Two oriented manifolds and are called oriented kobordant if there is an oriented manifold with ${\displaystyle M}$ ${\displaystyle N}$ ${\displaystyle W}$

${\displaystyle \partial W=M\cup {\overline {N}}}$

there, where the orientation refers to the orientation induced by the orientation on the edge and the manifold denotes the opposite orientation. ${\displaystyle \partial W}$ ${\displaystyle W}$ ${\displaystyle {\overline {N}}}$ ${\displaystyle N}$

Predictability

According to Thom's theorem, two manifolds are oriented co-ordinate if and only if all their Pontryagin numbers and Stiefel-Whitney numbers coincide.

Applications

Cobordism (oriented or unoriented) defines an equivalence relation , the equivalence classes can be understood as a group with the disjoint union .

René Thom's computation (of the torsion-free part) of the (oriented) cobordism group has numerous applications in algebraic topology and beyond. Hirzebruch's signature theorem followed directly from it, and the original proof of the Atiyah-Singer index theorem was based on it.

Within the topology, the term was fundamental to the development of the theory of surgery . Furthermore, the oriented cobordism groups are an example of a generalized cohomology theory .

The topological quantum field theory is also based on the concept of cobordism, see cobordism conjecture .

Variations of terms

Different variations of the term cobordism are significant, in particular framed cobordism (Pontryagin-Thom construction) and h-cobordism .

literature

• John Milnor : A survey of cobordism theory. Enseignement Math. (2) 8 1962 16-23. online (pdf)

Web links

• Steimle: What is cobordism?
• Anosov, Woizechowski: Bordism (Encyclopedia of Mathematics)

Individual evidence

1. ↑ Steimle, op.cit.
2. ↑ Thom, Quelques propriétés globales des variétés différentiables, Comm.Math.Helvetici, Volume 28, 1954, pp. 17-86, digitized