Cache-Oblivious Algorithm

A cache-oblivious algorithm is an algorithm that works efficiently on architectures with a multi-level memory hierarchy without knowing their exact parameters. These parameters are, for example, the number of caches , the size of the respective cache lines or their access times. The performance is analyzed in the so-called idealized cache model, in which the measure of costs is the cache misses. A cache-oblivious algorithm is optimal if it uses the caches asymptotically optimally, i.e. generates a minimum number of cache misses apart from constant factors.

The design goal is good performance of the same code on different machines with many memory tiers, without having to make adjustments to the architecture. (For optimal performance, however, adjustments to the respective hardware must be made that go beyond the memory hierarchy.)

Cache-oblivious algorithms are related to external memory algorithms , in which, however, only a two-level memory hierarchy is assumed and in which the size of the smaller / faster and the block size of the larger / slower memory are available to the algorithm as input parameters. An optimal cache-oblivious algorithm for two storage levels is also optimal for any number of storage levels. ${\displaystyle M}$ ${\displaystyle B}$

history

The first idea (and the name) for cache-oblivious algorithms comes from Charles E. Leiserson in 1996, the first publication is the master's thesis by Harald Prokop at the Massachusetts Institute of Technology from 1999. There, cache-oblivious algorithms are already being used Matrix transposition , for Fast Fourier Transformation and for sorting presented.

A large number of algorithms that can be described as cache-aware had already been developed beforehand. These also work optimally with the existing cache, but must know their parameters (size, line length).

Analysis in the idealized cache model

The idealized cache model. Cache has a size of memory words, the main memory is unlimited. Data transfer between the two always takes place in blocks of the size . ${\displaystyle M}$ ${\displaystyle B}$

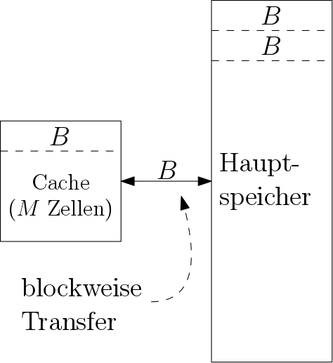
Cache-oblivious algorithms are analyzed in the Idealized Cache Model (alternatively the Cache Oblivious Model ). It is based on the RAM model . The processor works with a constant number of registers on an infinite main memory in which every memory cell in can be accessed. As an extension, a second memory level, the cache, is now inserted between the processor and the main memory. The other differences in the Idealized Cache model are: ${\displaystyle O(1)}$

• The main memory is divided into blocks of size . ${\displaystyle B}$
• The cache can contain memory words. This is assumed (so-called tall cache assumption ). ${\displaystyle M}$ ${\displaystyle M=\Omega (B^{2})}$
• A read / write operation between the processor and main memory can now be done through the cache. If this is not possible, it is called a cache miss .
• In the event of a cache miss: If a memory word located in a block of the main memory is to be accessed, the entire block is loaded into the cache. If the cache is already full, another block must first be displaced, i.e. written back from the cache to the main memory. ${\displaystyle w}$ ${\displaystyle x}$ ${\displaystyle x}$
• The cache has full associativity, which means that any block of memory can be loaded into any position in the cache.
• The displacement strategy is optimal. It is therefore assumed that the cache knows the exact sequence of all (including future) memory accesses and always displaces the block from the cache that is not accessed again until furthest in the future. This is of course an unrealistic assumption, but an LRU strategy approximates this up to a small constant factor.

The parameters and are not known to the algorithm. ${\displaystyle M}$ ${\displaystyle B}$

To analyze the complexity of an algorithm in the idealized cache model, only the cache misses are counted. This is justified by the very large differences in the access time between the various storage levels. The differences become more and more extreme with increasing storage capacity: For example, a register can be accessed in one clock cycle, access to a value in a cache takes just a few nanoseconds, and main memory access takes around 60–70 nanoseconds. The differences between mass storage media and removable storage media are even more extreme, where access times can range from milliseconds (for hard drives) to minutes (CDs, magnetic tapes).

Relationship to the external memory model and reality

In the external memory model, the parameters and are transferred to the algorithm as part of the input and it does not make any specifications about the cache displacement strategy. This enables the algorithm to use the existing hardware more efficiently by a constant factor. The analysis in the external memory model is very similar, here only the accesses to the external memory are counted. The advantage of an efficient algorithm in the Idealized cache model is that the same algorithm on machines with different and is efficient. In the same way, there is an efficiency over several storage levels in which the parameters and between different levels differ by orders of magnitude. ${\displaystyle M}$ ${\displaystyle B}$ ${\displaystyle M}$ ${\displaystyle B}$ ${\displaystyle M}$ ${\displaystyle B}$

The model of an ideal cache is much simpler than a real cache. Fast caches in particular (e.g. L1 caches) generally do not have full associativity for better performance . In addition, an optimal displacement strategy only exists in theory and must be approximated in practice. In many cases, however, the resulting differences in runtime can be demonstrably limited by small constant factors.

Examples

The upper matrix is ​​run through row by row, the lower one by column.

Many cache-oblivious algorithms operate on the divide and rule principle in which the issue is so far into smaller instances that the individual sub-problems fit in the cache. These can then be solved efficiently and reassembled in a cache-efficient method to form a solution for the original instance. This principle is also used for the following two algorithms.

Matrix transposition

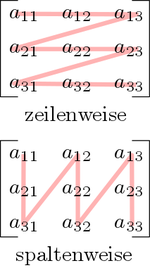
As a first example, a cache-oblivious algorithm for the transposition of a rectangular matrix, which goes back to Harald Prokop, is presented here. The input is in a matrix and the output is to be written in a matrix . A naive solution runs through rows and columns and copies a value from to in each step . If the matrices are sufficiently large, every access to the matrix, which is traversed in columns, leads to a cache miss. This gives an overall work of and cache complexity of . The cache-oblivious algorithm takes advantage of the fact that the transposing of the entire matrix can be divided into the transposing of two partial matrices. For this purpose, the matrix is ​​divided along the larger dimension into two (approximately) equally sized sub-matrices until the individual parts of the size fit twice in the cache (as input and output part matrix ). Then the sub-matrix can be transposed according to the naive method with work and cache complexity . Overall, the result is an optimal work of and cache complexity . Theoretically, the sub-matrices could be subdivided up to a size of further, in practice, however, a larger base case should be selected, since even the smallest caches are more than two memory words in size and the additional effort for subdivision dominates the cache effects in this order of magnitude. ${\displaystyle m\times n}$ ${\displaystyle A}$ ${\displaystyle n\times m}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle O(mn)}$ ${\displaystyle O(mn)}$ ${\displaystyle n'\times m'}$ ${\displaystyle O(n'm')}$ ${\displaystyle O(n'm'/B)}$ ${\displaystyle O(mn)}$ ${\displaystyle O(1+mn/B)}$ ${\displaystyle 1\times 1}$

Transpose a divide and conquer matrix. a) Transposition of matrix A as a whole. b) Transposition of the partial matrices and . ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$

sort by

As a further example, an optimal cache-oblivious algorithm for sorting is presented. Harald Prokop presented two of these in his master's thesis: Distribution Sort (based on Quicksort ) and Funnelsort. The latter is based on mergesort and should be described here:

Funnelsort sorts an array of entries recursively in two steps: ${\displaystyle n}$

1. Divide the array into sub-arrays, each of which is sized . Sort the sub-arrays recursively. ${\displaystyle n^{1/3}}$ ${\displaystyle n^{2/3}}$
2. Merge the sorted sub-arrays with a merger. ${\displaystyle n^{1/3}}$

So the entire complexity lies in the merger, which is also called a funnel . A merger receives sorted sequences as input and, with each call, outputs the next elements of the sorted sequence that results from the merging of the input sequences. In contrast to mergesort, merging is also done recursively with Funnelsort. This recursive decomposition of the merge operation means that the individual sub-problems will eventually fit into the cache. ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k^{3}}$

A -Merger is recursively composed of several -Merger (the figure on the right shows a 9-Merger): There are a total of input mergers over which the inputs are evenly distributed. Each input merger writes its output into its own buffer of the size . There is also an output merger whose inputs are connected to the buffers of and whose output is also the output of the -Merger. Each of the built-in mergers has inputs and produces an output of elements. ${\displaystyle k}$ ${\displaystyle {\sqrt {k}}}$ ${\displaystyle {\sqrt {k}}}$ ${\displaystyle I_{1},I_{2},\ldots ,I_{\sqrt {k}}}$ ${\displaystyle k}$ ${\displaystyle 2k^{3/2}}$ ${\displaystyle O}$ ${\displaystyle I_{1},I_{2},\ldots ,I_{\sqrt {k}}}$ ${\displaystyle k}$ ${\displaystyle {\sqrt {k}}}$ ${\displaystyle {\sqrt {k}}}$ ${\displaystyle k^{3/2}}$

When calling the merger, elements must now be output. For this purpose, the output merger is called a total of times, which outputs further elements in each call . Before each call, it is ensured that each buffer contains at least elements in the input . If this is not the case with buffer , input merger is called first , which writes new elements into the buffer. The size of the buffer was chosen so that there is always enough space. ${\displaystyle k}$ ${\displaystyle k^{3}}$ ${\displaystyle O}$ ${\displaystyle k^{2/3}}$ ${\displaystyle k^{3/2}}$ ${\displaystyle O}$ ${\displaystyle k^{3/2}}$ ${\displaystyle j}$ ${\displaystyle I_{j}}$ ${\displaystyle k^{3/2}}$

Brodal and Fagerberg also describe a variant of Lazy Funnelsort in which a buffer is only refilled when it is completely empty. This can be a little faster in practice. The authors prove that in theory there are the same number of cache misses.

See also

• Storage hierarchy
• External memory algorithm

A 9 merger, consisting of four 3 mergers (input merger and output merger ). ${\displaystyle I_{1},I_{2},I_{3}}$ ${\displaystyle O}$

Individual evidence

1. ↑ ^{a b c d} Harald Prokop. Cache-Oblivious Algorithms . Masters thesis, MIT. 1999.
2. ↑ Erik D. Demaine: Cache-Oblivious Algorithms and Data Structures . In: MIT Laboratory for Computer Science . 2000.
3. ↑ Piyush Kumar: Cache-Oblivious Algorithms Archived from the original on July 11, 2012. In: Springer Verlag (Ed.): Algorithms for Memory Hierarchies . September, pp. 193-212.
4. ↑ ^{a b} , CE Leiserson, H. Prokop, S. Ramachandran: Cache-oblivious algorithms . In: Proc. IEEE Symp. On Foundations of Computer Science (FOCS)., Pp. 285-297.
5. ^ Daniel Sleator, Robert Tarjan. Amortized Efficiency of List Update and Paging Rules. In Communications of the ACM , Volume 28, Number 2, pp.202-208. Feb 1985.
6. ↑ Gerth Brodal, Rolf Fagerberg: Cache Oblivious Distribution Sweeping . In: Springer Verlag (Ed.): Proceedings of the 29th International Colloquium on Automata, Languages, and Programming . No. 2380 of Lectrue Notes in Computer Science, September, pp. 426-438.