Crystal ball function

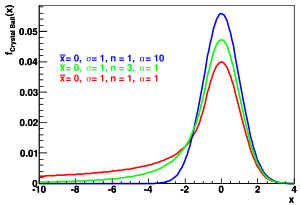
Plot of the Crystal Ball function with three different parameter sets

The Crystal Ball function , named after the Crystal Ball Collaboration , is a density function of an asymmetrical probability distribution that is often used to model various lossy processes in high energy physics . It is composed of a Gaussian-shaped central area, which turns into a power law for small values . The function itself and its first derivative are continuous .

The crystal ball function is given by

${\displaystyle f(x;\alpha ,n,{\bar {x}},\sigma )=N\cdot {\begin{cases}\exp \left(-{\frac {(x-{\bar {x}})^{2}}{2\sigma ^{2}}}\right),&{\mbox{falls }}{\frac {x-{\bar {x}}}{\sigma }}>-\alpha \\A\cdot \left(B-{\frac {x-{\bar {x}}}{\sigma }}\right)^{-n},&{\mbox{falls }}{\frac {x-{\bar {x}}}{\sigma }}\leqslant -\alpha \end{cases}}}$

With

${\displaystyle A=\left({\frac {n}{\left|\alpha \right|}}\right)^{n}\cdot \exp \left(-{\frac {\left|\alpha \right|^{2}}{2}}\right)}$

${\displaystyle B={\frac {n}{\left|\alpha \right|}}-\left|\alpha \right|}$

${\displaystyle N={\frac {1}{\sigma (C+D)}}}$

${\displaystyle C={\frac {n}{\left|\alpha \right|}}\cdot {\frac {1}{n-1}}\cdot \exp \left(-{\frac {\left|\alpha \right|^{2}}{2}}\right)}$

${\displaystyle D={\sqrt {\frac {\pi }{2}}}\left(1+\operatorname {erf} \left({\frac {\left|\alpha \right|}{\sqrt {2}}}\right)\right).}$

Here, (Skwarnicki 1986) a normalization factor, and are expected value and standard deviation of the Gaussian distribution, determines the position of the transition between the Gaussian distribution and power law and the free parameter is the power law. erf is the error function . ${\displaystyle N}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle \sigma }$ ${\displaystyle \alpha }$ ${\displaystyle n}$

literature

• JE Gaiser, Appendix-F Charmonium Spectroscopy from Radiative Decays of the J / Psi and Psi-Prime, Ph.D. Thesis , SLAC-R-255 (1982), p. 178. (PDF, 205 pages; 6.5 MB)
• MJ Oreglia, A Study of the Reactions psi prime → gamma gamma psi, Ph.D. Thesis , SLAC-R-236 (1980), Appendix D.
• T. Skwarnicki, A study of the radiative CASCADE transitions between the Upsilon-Prime and Upsilon resonances, Ph.D Thesis (PDF; 41.7 MB), DESY F31-86-02 (1986), Appendix E.