Davies equation

The Davies equation is an equation for estimating activity coefficients and thus activities in aqueous solutions of salts ( electrolyte ). The equation was first proposed by Cecil Whitfield Davies in 1938 and later underpinned by further work by him and is therefore named after him. It is based on the results of the Debye-Hückel theory , which is valid for dilute solutions. It extends their equation for the activity coefficients so that they can also be used for more concentrated solutions; the extension was found purely empirically. The equation is widely used to calculate chemical equilibria and is implemented in many related programs.

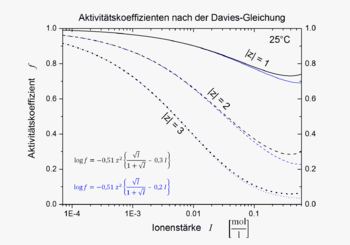
The Davies equation gives the relationship between the ionic strength I of a solution and the mean value of the ionic activity coefficient f (or its decadic logarithm). At temperatures around 25 ° C the equation is:

${\displaystyle \lg f_{i}=-0{,}5\cdot z_{i}^{2}\left({\frac {\sqrt {I}}{1+{\sqrt {I}}}}-0{,}3\cdot I\right)}$

With

• I : numerical value of the ionic strength without the unit mol / liter ${\displaystyle I={\frac {1}{2}}\sum _{i}c_{i}\cdot z_{i}^{2}}$
• z _i : number of charges of the ions

Activity coefficients as a function of the ionic strength at 25 ° C, calculated with two variants of the Davies equation and in a simple logarithmic representation. The equations used are given. Black: coefficient for the linear term 0.3. Blue: coefficient 0.2.

The Davies equation is a good approximation for ionic strengths from 0 to about 0.5 mol / l; this is a significantly larger range than that of the extended Debye-Hückel limit law, which  is valid up to about 10 ⁻² mol / l. The Davies equation is hardly suitable for more concentrated solutions with I > 0.5 mol / l. In this case, other relationships, e.g. B. the Pitzer applied.

Activity coefficients according to the Davies equation as a function of the ionic strength at 25 ° C in a linear representation.

Compared to the corresponding result of the Debye-Hückel theory, another simple term was added in which the ionic strength is linearly included. The coefficient in the linear term was originally given by Davies as 0.2 and later changed to 0.3. The Davies equation gives the same activity coefficient for all ions with the same charge; the size of the ions does not go into it. It is usually less precise than more specific equations with multiple parameters.

Extended Davies Equation

The equation originally proposed by Davies is valid for 25 ° C. More general, the Davies equation is in the form

${\displaystyle \lg f_{i}=-A\cdot z_{i}^{2}\left({\frac {\sqrt {I}}{1+{\sqrt {I}}}}-0{,}3\cdot I\right)}$

with the temperature-dependent parameter A , which is taken from the Debye-Hückel theory. The formula for calculating the parameter and values ​​are given here . In this equation, too, the numerical value 0.2 is sometimes used instead of 0.3. Some authors recommend the value 0.1 instead.

Historical

Even Erich Hückel had suggested Hückel limiting law Debye to add the extended a linear term, and Edward Guggenheim had discussed appropriate equations. For example, for hydrochloric acid HCl (aq), for which the ionic strength I is equal to the concentration c , the equation applies up to a one-molar solution:

${\displaystyle \lg f_{H,Cl}=-{\frac {0{,}50{\sqrt {c}}}{1+1{,}40{\sqrt {c}}}}+0{,}136\cdot c}$

In 1936 Guggenheim gave an equation for monovalent ions ( I = c ) that contains a linear term with a parameter λ that depends on the type of ion. It can be written as

${\displaystyle \lg f_{i}=-A{\frac {\sqrt {c}}{1+{\sqrt {c}}}}+\lambda \cdot c}$,

where = 0.5 at 15 ° C to 25 ° C and = 0.486 at 0 ° C. This equation is now also called the Guggenheim equation. Building on this, Davies suggested his equation as an approximation, using a value instead of the ion-specific parameter λ that resulted from the mean of the λ values ​​known at the time. ${\displaystyle A}$ ${\displaystyle A}$

Applications

The Davies equation is z. B. used in geochemistry , especially in soil science , also in hydrochemistry .

More concentrated solutions

For electrolytes with a higher concentration, equations with additional, substance-dependent parameters, e.g. B. the Bromley equation or the Pitzer equations developed by Kenneth Pitzer .

Individual evidence

1. ^ ^{A b c} Cecil Whitfield Davies : 397. The extent of dissociation of salts in water. Part VIII. An equation for the mean ionic activity coefficient of an electrolyte in water, and a revision of the dissociation constants of some sulphates . In: The Chemical Society (Ed.): Journal of the Chemical Society (Resumed) . 1938, p. 2093-2098 , doi : 10.1039 / JR9380002093 .
2. ^ ^{A b} Cecil Whitfield Davies Davies, Ion Association. London: Butterworths 1962. pp. 37-53.
3. ↑ 6.6.A.3 Davies Equation in: James W. Murray, Chapter 6 Activity Scales and Activity Corrections
4. ↑ Rudolf Brdicka, fundamentals of physical chemistry, 15. Edited Edition, Edited by Jiri Dvorak, German Academic Publishers, Berlin 1990, page 583rd
5. ^ Stefan Doeller: Calculation of Proton Activity in Aqueous Protolyte Solutions . In: Analytica Chimica Acta . tape 115 , March 15, 1980, pp. 261–268 , doi : 10.1016 / S0003-2670 (01) 93164-2 ( sciencedirect.com [accessed June 5, 2016]).
6. ^ ^{A b} Edward A. Guggenheim: L. The specific thermodynamic properties of aqueous solutions of strong electrolytes . In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . Series 7th volume 19 , no. 127 . Taylor & Francis, 1935, ISSN  1941-5990 , pp. 588-643 , doi : 10.1080 / 14786443508561403 (English).
7. ^ Edward A. Guggenheim: XXVII. Specific thermodynamic properties of aqueous solutions of uni-univalent electrolytes . In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science Series 7 . tape 22 , no. 146 . Taylor & Francis, 1936, ISSN  1941-5990 , pp. 322–336 , doi : 10.1080 / 14786443608561690 (English, tandfonline.com [PDF]).
8. ↑ Questions and answers on the PHREEQC geochemistry program
9. ↑ Hans-Peter Blume, Gerhard W. Brümmer, Rainer Horn, Ellen Kandeler, Ingrid Kögel-Knabner, Ruben Kretzschmar, Karl Stahr, Berndt-Michael Wilke: Scheffer / Schachtschabel: Textbook of soil science . 16th edition. Springer-Verlag, Spektrum Akademischer Verlag, Heidelberg 2010, ISBN 978-3-8274-1444-1 , 5.3.1. Ionic strength, concentration and activity, p. 126 ( limited preview in Google Book Search [accessed June 5, 2016]).
10. ^ Donald L. Sparks: Soil Physical Chemistry . Second edition. CRC Press, Boca Raton, Boston, London New York 1998, ISBN 0-87371-883-6 , Chapter 3, Thermodynamics of the Soil Solution, 3. Davies equation, pp. 113 (English, preview on Google Books [accessed on May 26, 2016]).
11. ↑ Harald Kalka: 2.5 Non-ideal solutions and activity models. (pdf; 1.4 MB) In: aquaC - aquatical chemistry, operating instructions for the program. UIT GmbH, August 2003, pp. 12–13 , accessed on June 5, 2016 . 
12. ↑ Harald Kalka: Activity coefficient and activity models. In: water chemistry. Retrieved June 5, 2016 .