Deformation invariants

In continuum mechanics, the deformation invariants denote the three main invariants of the right or left Cauchy-Green deformation tensor . They represent the coefficients of the characteristic polynomial in the main axis transformation of the distance tensor. At the same time, according to Vieta's theorem , they can also be expressed by the main extensions: ${\displaystyle I_{1},I_{2},I_{3}}$ ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$

${\displaystyle {\begin{array}{lclcl}I_{1}&=&\mathrm {Spur} (\mathbf {b} )&=&\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&=&\mathrm {Spur} (\mathbf {b} ^{-1})\,\det(\mathbf {b} )&=&\lambda _{1}^{2}\,\lambda _{2}^{2}+\lambda _{1}^{2}\,\lambda _{3}^{2}+\lambda _{2}^{2}\,\lambda _{3}^{2}\\I_{3}&=&\det(\mathbf {b} )&=&\lambda _{1}^{2}\,\lambda _{2}^{2}\,\lambda _{3}^{2}\end{array}}}$

With

• ${\displaystyle \mathbf {b} }$ the deformation tensor
• ${\displaystyle \mathrm {Spur} (\mathbf {b} )}$the trace of the deformation tensor,
• ${\displaystyle \det(\mathbf {b} )}$the determinant of the deformation tensor,
• ${\displaystyle \mathbf {b} ^{-1}}$the inverse of the deformation tensor and
• ${\displaystyle \lambda _{1,2,3}^{2}=\eta _{1,2,3}}$ the eigenvalues ​​of the deformation tensor.

The above relationships apply to the left Cauchy-Green tensor and the right Cauchy-Green tensor , because both tensors have due ${\displaystyle \mathbf {b} :=\mathbf {F\cdot F^{\top }} }$ ${\displaystyle \mathbf {C} :=\mathbf {F^{\top }\cdot F} }$

${\displaystyle \mathbf {b} \cdot {\vec {v}}=\eta {\vec {v}}\quad \Leftrightarrow \quad \mathbf {F^{\top }\cdot b} \cdot {\vec {v}}=\mathbf {F^{\top }\cdot F\cdot F^{\top }} \cdot {\vec {v}}=\mathbf {C\cdot (F^{\top }} \cdot {\vec {v}})=\eta (\mathbf {F^{\top }} \cdot {\vec {v}})}$

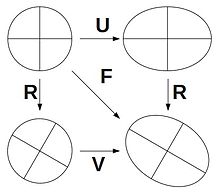
Illustration of the polar decomposition

the same eigenvalues ​​and thus also the same invariants, which makes them mathematically similar to one another . The tensor F is the deformation gradient . The same applies to the symmetrical , positively definite , right and left deformation tensors U and v , which are according to

${\displaystyle \mathbf {F} =\mathbf {R\cdot U} =\mathbf {v\cdot R} .}$

result from the polar decomposition of the deformation gradient, see picture. Here R is an actually orthogonal tensor with the properties R ^T · R = 1 and det ( R ) = +1 ( 1 is the unit tensor .) The right and left deformation tensor have due

${\displaystyle \mathbf {v} \cdot {\vec {v}}=\lambda {\vec {v}}\quad \Leftrightarrow \quad \mathbf {b} \cdot {\vec {v}}=\mathbf {F\cdot F^{\top }} \cdot {\vec {v}}=\mathbf {v\cdot R\cdot R^{\top }\cdot v^{\top }} \cdot {\vec {v}}=\lambda \mathbf {v} \cdot {\vec {v}}=\lambda ^{2}{\vec {v}}}$

the main elongations λ _1,2,3 as eigenvalues, because they are also similar to each other:

${\displaystyle \mathbf {R^{\top }\cdot v} \cdot {\vec {v}}=\mathbf {R^{\top }\cdot v\cdot R\cdot R^{\top }} \cdot {\vec {v}}=\mathbf {R^{\top }\cdot R\cdot U\cdot R^{\top }} \cdot {\vec {v}}=\mathbf {U\cdot (R^{\top }} \cdot {\vec {v}})=\lambda (\mathbf {R^{\top }} \cdot {\vec {v}}).}$

Because the deformation gradient is always and everywhere invertible, so are the distance sensors.

The third invariant also represents the square of the volume ratio : ${\displaystyle J:=\operatorname {det} (\mathbf {F} )}$

${\displaystyle I_{3}(\mathbf {b} )=I_{3}(\mathbf {C} )=J^{2}=I_{3}^{2}(\mathbf {v} )=I_{3}^{2}(\mathbf {U} ).}$

If the material behavior is incompressible ( ), the third invariant of the distance sensors remains the same as the identity. ${\displaystyle J=1}$

literature

• H. Altenbach: Continuum Mechanics . Springer, 2012, ISBN 978-3-642-24118-5 .