Dyson-Schwinger equations

The Dyson-Schwinger equations (DSGn), also Schwinger-Dyson equations, are relations between various Green functions of a quantum field theory found by Freeman Dyson and Julian S. Schwinger . Since they represent the equations of motion for Green's functions, they are also often called the Euler-Lagrange equations of a quantum field theory. There are an infinite number of functional differential equations that are all, directly or indirectly, coupled to one another. That is why one often speaks of the infinite tower of the Dyson-Schwinger equations.

The Dyson equations derived by Dyson by adding up an infinite number of Feynman diagrams were extended by Schwinger in his quantum action principle to all Green's functions of any quantum field theory. Dyson-Schwinger equations can be found for all n-point functions. The most important, however, are the equations for the 2-point and 3-point functions, the solutions of which are propagators and vertices . The 4-point function presented by Schwinger is a generalization (inhomogeneous form) of the Bethe-Salpeter equation .

The idea behind the DSGn is that the interactions of a theory are also reflected in its Green functions or S-matrix elements . These "dressed" or full Green functions, that is, those that contain the interactions, should contain the associated bare (= interaction-free) Green functions in the limit of free theories and interaction-dependent terms. The DSGn are a guide to how and which interacting terms are to be taken into account.

The Dyson-Schwinger equations provide access to phenomena that are not accessible with conventional perturbation theory . In the area of quantum chromodynamics , for example, this is the low-energy area, since the coupling constant becomes large here . ${\displaystyle (\alpha >1)}$

Examples: quantum electrodynamics

A graphical representation of the Dyson-Schwinger equations of quantum electrodynamics for the electron propagator, photon propagator, and electron-photon vertex.

In quantum electrodynamics these equations come up again and again:

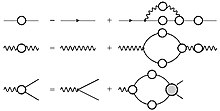
The Dyson-Schwinger equation of the electron propagator ${\displaystyle S(p)}$

${\displaystyle S(p)=S_{0}(p)+S_{0}(p)*\left(e^{2}\int {\frac {d^{4}k}{(2\pi )^{4}}}\gamma _{\mu }D^{\mu \nu }(p-k)S(k)\Gamma _{\nu }(p,k)\right)*S(p)}$,

of the photon propagator ${\displaystyle D^{\mu \nu }(p)}$

${\displaystyle D^{\mu \nu }(p)=D_{0}^{\mu \nu }(p)+D_{0}^{\mu \nu '}(p)*{\Bigl (}-e^{2}\operatorname {tr} {\Bigl [}\int {\frac {d^{4}k}{(2\pi )^{4}}}\gamma _{\nu '}S(k)\Gamma _{\mu '}(k,k+p)S(k+p){\Bigr ]}{\Bigr )}*D^{\mu '\nu }(p)}$,

and the electron-photon vertex ${\displaystyle \Gamma _{\nu }(p',p)}$

${\displaystyle \Gamma _{\nu }(p',p)=\Gamma _{\nu \,0}(p',p)+\int {\frac {d^{4}k}{(2\pi )^{4}}}S(p'+k)\Gamma _{\nu }(p'+k,p+k)S(p+k)K(p+k,p'+k,k)}$.

Here the quantities with a subscript 0 denote the free terms, i.e. for vanishing interaction. refers to the four-electron interaction nucleus, i.e. the four-electron T-matrix. ${\displaystyle K(p+k,p'+k,k)}$

Using these examples, some important properties of the DSGs can be shown. An interaction term is added to the free term. You can also see that to solve the electron propagator you need the clothed photon propagator, which is itself the solution of your own DSG. For both you need the clothed electron-photon vertex, which in turn couples to the four-electron nucleus, which in turn has to satisfy its own DSG. So all DSG are directly or indirectly coupled to each other and an infinite tower of coupled equations is formed. If you want to solve these equations practically, you have to cut off this tower at a certain point (truncate) and model the missing terms with approaches or the like.

If you identify the terms in brackets with the electron or photon self-energy, you can find the original Dyson equations in the above equations .

Derivation

There are different derivations for the Dyson-Schwinger equations. While in the original publication Schwinger derived the DSGn with the help of his quantum action principle, the path integral formalism is mostly used today .

Analogous to the Euler-Lagrange equations , it is assumed that the path integral of the underlying quantum field theory is invariant under an infinitesimal transformation of the fields . To simplify matters, we assume here a theory of a field . In the case of multiple fields, such as B. in the case of the QED above, the fields and their sources must be marked (indexed). However, nothing changes in the general ideas of the derivation. So ${\displaystyle \phi }$ ${\displaystyle \phi }$

${\displaystyle Z[J]=\int {\mathcal {D}}\phi \,\exp \left(iS(\phi )+iJ\phi \right)=\int {\mathcal {D}}\phi '\,\exp \left(iS(\phi ')+iJ\phi '\right)}$

where , with an infinitesimal shift , and represents the functional integral over all field configurations (similar to the partition function of statistical physics), the effect of the theory and the sources of the fields. This condition can now be translated into the requirement that an integration disappears via a derivation according to the fields: ${\displaystyle \phi '=\phi +\chi }$ ${\displaystyle \chi }$ ${\displaystyle Z[J]}$ ${\displaystyle S(\phi )}$ ${\displaystyle J}$

${\displaystyle 0=\int {\mathcal {D}}\phi {\frac {\partial }{\partial \phi }}\,\exp \left(iS(\phi )+iJ\phi \right)=\int {\mathcal {D}}\phi \,\exp \left(iS(\phi )+iJ\phi \right)\,\left({\frac {i\partial S(\phi )}{\partial \phi }}+iJ\right)}$

Now the bracket can be pulled in front of the integral. The fields in the effect then have to be replaced by derivatives and one obtains

${\displaystyle 0=\left({\frac {i\partial S({\tfrac {\partial }{i\partial J}})}{\partial \phi }}+iJ\right)\,\int {\mathcal {D}}\phi \,\exp \left(iS(\phi )+iJ\phi \right)}$

And you get the Master-Dyson-Schwinger equation for the full Green functions

${\displaystyle 0=\left({\frac {\partial S({\tfrac {\partial }{i\partial J}})}{\partial \phi }}+J\right)\,Z[J]\qquad (1)}$

All other Dyson-Schwinger equations for the full Green functions can now be generated from it by a functional derivation according to the fields.

The Dyson-Schwinger equations for the connected Green functions are obtained with the help of the general relationship and the definition for the generating function of the connected Green functions can be transformed into equation (1) ${\displaystyle f\left({\tfrac {\partial }{\partial x}}\right)\exp \left(F(x)\right)=\exp \left(F(x)\right)\,f\left({\tfrac {\partial }{\partial x}}+{\tfrac {\partial \,F(x)}{\partial x}}\right)\cdot 1}$ ${\displaystyle W[J]=-i\,\log {Z[J]}}$

${\displaystyle 0=\left({\frac {\partial S({\tfrac {\partial }{i\partial J}})}{\partial \phi }}+J\right)\,\exp \left(iW[J]\right)=\exp \left(iW[J]\right)\,\left({\frac {\partial S({\tfrac {\partial }{i\partial J}}+{\tfrac {\partial W[J]}{\partial J}})}{\partial \phi }}+J\right)\cdot 1}$

and receives

${\displaystyle {\frac {\partial }{\partial \phi }}S\left({\frac {\partial }{i\partial J}}+{\frac {\partial W[J]}{\partial J}}\right)\cdot 1=-J\qquad (2)}$

The generating functional of the 1-particle irreducible Green functions is called the effective effect and is usually denoted by the symbol , where the index _cl indicates that it is not the original fields but their expected vacuum values . The effective action is the generating function as a generalized Legendre transformation defined . Then, similar to the above, the master DSG for the 1-particle irreducible Green functions can be derived: ${\displaystyle \Gamma [\phi _{cl}]}$ ${\displaystyle \phi }$ ${\displaystyle W[J]}$ ${\displaystyle \Gamma [\phi _{cl}]=W[J]+J\cdot \phi _{cl}}$

${\displaystyle {\frac {\partial }{\partial \phi }}S\left(\phi _{cl}+i\left({\frac {\partial ^{2}\Gamma }{\partial \phi _{cl}\,\partial \phi _{cl}}}\right)^{-1}{\frac {\partial }{\partial \phi _{cl}}}\right)\cdot 1={\frac {\partial \Gamma }{\partial \phi _{cl}}}\qquad (3)}$

With equations (1), (2) and (3) we now have the Master-Dyson-Schwinger equations. The respective Dyson-Schwinger equations of the n-point Green functions are calculated by functional derivatives of these equations.

Applications in current research

In current research, the Dyson-Schwinger equations are used to calculate Green functions such as B. Calculate quark or gluon propagators in the QCD. It is also possible to use clever combinatorics to determine which proportions are dominant in the low-energy range. So one hopes to draw conclusions, e.g. B. on the long-range behavior of the strong interaction, which is closely related to the confinement problem.

Together with the Bethe-Salpeter equation , self-consistent properties of bond states can be calculated. This is mainly used to determine the masses and electromagnetic form factors of mesons and baryons .

literature

The two standard references on this subject (both in English) are:

• Claude Itzykson, Jean-Bernard Zuber: Quantum Field Theory . McGraw-Hill , 1980.
• RJ Rivers: Path Integral Methods in Quantum Field Theories . Cambridge University Press, 1990.

Eric Swanson gave introductory lectures on DSGn and Functional Methods at summer schools in 2010. He has published a script on the arXiv:

• Eric Swanson: A Primer on Functional Methods and the Schwinger-Dyson Equations . In: Lectures presented at Hadron XI, Maresias, Brazil and HUGS, Jefferson Lab, USA, (2010) . August. arxiv : 1008.4337v2 .

There are two review articles on applications in quantum chromodynamics :

• R. Alkofer and L. v.Smekal: On the infrared behavior of QCD Green's functions . In: Phys. Rept. . 353, 2001, p. 281. doi : 10.1016 / S0370-1573 (01) 00010-2 .
• CD Roberts and AG Williams: Dyson-Schwinger equations and their applications to hadron physics . In: Prog. Part. Nucl. Phys. . 33, 1994, p. 477. doi : 10.1016 / 0146-6410 (94) 90049-3 .

Individual evidence

1. ^ F. Dyson: The S Matrix in Quantum Electrodynamics . In: Phys. Rev. . 75, 1949, p. 1736. doi : 10.1103 / PhysRev . 75.1736 .
2. ↑ ^{a b c} J. Schwinger: On Green's functions of quantized fields I + II . In: PNAS . 37, 1951, pp. 452-459. doi : 10.1073 / pnas.37.7.452 . and doi : 10.1073 / pnas.37.7.455
3. ↑ CD Roberts and AG Williams: Dyson-Schwinger equations and their applications to hadron physics . In: Prog. Part. Nucl. Phys. . 33, 1994, p. 477. doi : 10.1016 / 0146-6410 (94) 90049-3 .
4. ^ RJ Rivers: Path Integral Methods in Quantum Field Theories . Cambridge University Press, 1990.
5. ↑ ^{a b} Peskin, Michael E. and Schroeder, Daniel V .: An Introduction to Quantum Fields . Westview Press, 1995, ISBN 0-201-50397-2 .
6. ↑ L. Ryder: Quantum Field Theory . Cambridge University Press, 1985.
7. ↑ ^{a b} Eric Swanson: A Primer on Functional Methods and the Schwinger-Dyson Equations . In: Lectures presented at Hadron XI, Maresias, Brazil and HUGS, Jefferson Lab, USA, (2010) . August. arxiv : 1008.4337v2 .
8. ↑ R. Alkofer and L. v.Smekal: On the infrared behavior of QCD Green's functions . In: Phys. Rept. . 353, 2001, p. 281. doi : 10.1016 / S0370-1573 (01) 00010-2 .
9. ^ P. Maris and P. Tandy: QCD modeling of hadron physics . In: Nuclear Physics B . 161, 2006, p. 136. doi : 10.1016 / j.nuclphysbps.2006.08.012 .
10. ↑ G. Eichmann et al .: A Covariant view on the nucleons' quark core . In: Annals of Physics . 323, No. 10, 2008, pp. 2505-2553. doi : 10.1016 / j.aop.2008.02.007 .