Uniform continuity
A uniformly continuous function is a term from the mathematical branch of analysis . Uniform continuity of a function is a stronger condition than that of the continuity of a function . In the case of a uniformly continuous function, the distance between any pairs of function values is smaller than any given maximum error, as long as the arguments are sufficiently close to one another.
definition
Be a subset of , short .
A mapping is called uniformly continuous if and only if
- .
For a better differentiation, the usual continuity , if it is given in every point of , is also called point-wise continuity .
The peculiarity of the uniform continuity is that it only depends on and not, as with point-by-point continuity, additionally on the position .
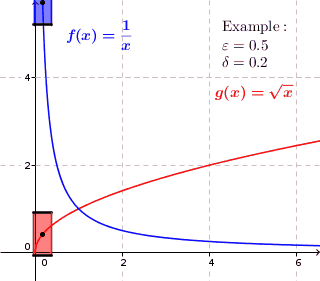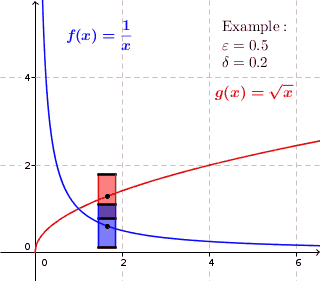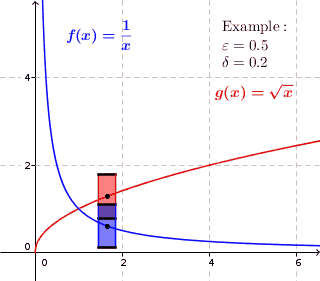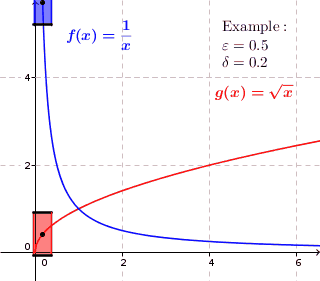
This clearly means: For every vertical rectangle side , no matter how small , you can find a sufficiently small horizontal rectangle side so that if you move the rectangle with the sides along the function graph, it only cuts the vertical rectangle sides . (Ex .: root function open ).
Examples
Consider the function
- with :
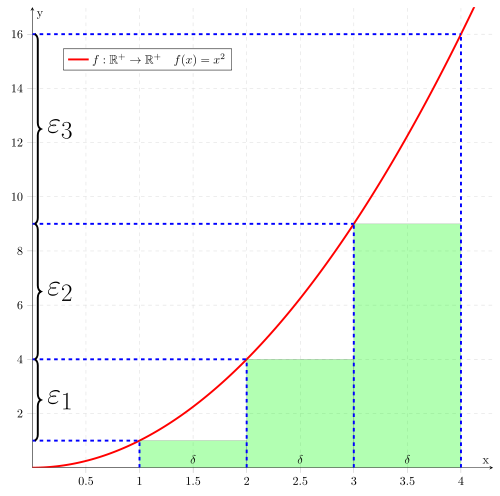
This is continuous, but not evenly continuous: the further to the right you choose two points in one of the stripes, the greater the distance between the two function values can be and thus exceed our selected one . This does not correspond to the definition of uniform continuity: the distance between the function values must be smaller than a specified one for each choice of two such positions . This is not the case with this function.
Furthermore, every restriction from to a compact interval is uniformly continuous. This follows directly from Heine's theorem .
Another example is the continuous function
- With
which is evenly steady, even Hölder steady , but not lipschitz steady .
Generalization: metric spaces
The following definition is also used more generally:
Let be two metric spaces. A mapping is called uniformly continuous if and only if
- .
Generalization: uniform spaces
Even more generally, in topology, a function is called a function between two uniform spaces and uniformly continuous if the archetype of each neighborhood is a neighborhood again, i.e. if
properties
Every uniformly continuous function is continuous. The reverse is not true: There are continuous functions like the square function that are not uniformly continuous. For certain domains of definition, continuity and uniform continuity coincide. The Heine theorem says: Every continuous function on a compact set is uniformly continuous.
If there is a Cauchy sequence in space and is uniformly continuous, then there is also a Cauchy sequence in . This generally does not apply to functions that are only continuous, as the example and shows.
Immediately from the fact that Cauchy sequences are mapped to Cauchy sequences, it now follows: If is uniformly continuous on a set , then it can be continuously continued on the closure .
In , the statement can clearly be made that a uniformly continuous function (with values in ) cannot have any poles. How should it, since it can - as already shown - be continued steadily towards the end of its domain of definition. Such a continuous continuation is just not possible in a pole.
Special forms of uniform continuity are Hölder and Lipschitz continuity .
Visualization
In a uniformly continuous function for each predetermined maximum error an all pairs are found, then that function values and a maximum difference, as long as the distances from and smaller than shown. Accordingly, a rectangle with height and width can be drawn around each point of the graph , in which the graph runs completely inside the rectangle, so that no function values are directly above or below the rectangle. This is not possible for functions that are not uniformly continuous. In part, the graph runs inside the rectangle - but not everywhere.
See also
Web links
swell
- Konrad Königsberger : Analysis 1 . Springer-Verlag, Berlin et al., 2004, ISBN 3-540-41282-4 .
- Konrad Königsberger : Analysis 2. Springer-Verlag, Berlin / Heidelberg, 2000, ISBN 3-540-43580-8 .
- Otto Forster : Analysis Volume 1: Differential and integral calculus of a variable. Vieweg-Verlag, 8th edition 2006, ISBN 3-528-67224-2 .






























![M = (0,1], f (x) = {\ tfrac 1x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ac572438abcab4380d79dc10bb12c42ed6c3e)











