Hindu lunisolar calendar

The Hindu lunisolar calendar exists in a great variety and regional variants. This article therefore only presents the basic principles on which all lunisolar calendars are based.

history

The oldest references to chronology on the Indian subcontinent can be found in the Vedas , the oldest parts of which date back to around 1200 BC. Go back BC. The Jyotisha Vedanga with treatises on astronomy and astrology comes from a later period . Greek and Babylonian knowledge influenced the Siddhantas (astronomical textbooks) in the first centuries AD . The three most important are probably the oldest Surya-Siddhanta , the Arya-Siddhanta of the astronomer Aryabhata I (476 - around 550 AD) and the Brahma-Siddhanta of Brahmagupta (598 - 668).

Up until around AD 1100, the calendar calculation was based on the mean movement of the sun and moon, later reference was made to the apparent movement of the sun and moon.

The year

The lunisolar year is a lunar year linked to the sidereal solar year with twelve or thirteen months. This results in a common year ( samvatsara mana ) with twelve months a length of 354 or 355 days and for a leap year (adhika samvatsara ) with thirteen months a length of 383, 384 or 385 days.

There are two forms of the year. If - as above all in northern India - the months last from one full moon to the next full moon, the year is a purnimanta year, if - as especially in the south of the country - the months last from one new moon to the next new moon, that is Year an amanta year.

The year count

The years are counted as elapsed years after the Kali Yuga era and as current years after the Vikrama Samvat era .

The beginning of the year

The year begins almost everywhere in India with the last new moon, before the sun enters the sign mesha (Aries). Such a year is called chaitrada . In Gujarat, the year begins with the new moon, before the sun enters the sign tula (Libra). Such a year is called a karttikadi . Since the year always begins with a new moon, a purnimanta year therefore begins in the middle of a month.

The precision

Since the lunar year is linked to the sidereal year, it is on average as long as the sidereal year, the length of which the Surya-Siddhanta states as 365.2587558 days. The other Siddhantas give a slightly different value. Since the length of the sidereal year is actually 365.2563042 days, i.e. the Surya-Siddhanta year is 0.0024516 days longer, it is shifted by 1 ° in around 400 years compared to the fixed stars. While the reference point around the year 285 AD was the star chaitra (Spica, αVir), today it is the star τVir. Because of the precession of the earth's axis , the vernal equinox shifts towards the fixed star sky, and today the sun faces the star τVir around mid-April. The beginning of the lunisolar year currently falls between mid-March and mid-April. The following table shows the beginning of the year for the next few years. Because of the many variants of the calendar invoice, the actual date may differ by a day or two.

Kali Yuga	Vicrama Samvat	Gregorian
5116	2071	March 31, 2014
5117	2072	March 20, 2015
5118	2073	April 7, 2016
5119	2074	March 28, 2017
5120	2075	17th March 2018
5121	2076	5th April 2019
5122	2077	March 24, 2020

The month

The civil month is to be distinguished from the lunar month.

The lunar month

A lunar month begins with a new moon or a full moon. If the month begins and ends with a new moon, it is an amana masa , if it begins and ends with a full moon, it is a purnimanta masa .

A lunar month consists of 30 lunar days (see below), which are divided into two halves of 15 lunar days each: The light half with the waxing moon, which begins at the new moon and ends at the full moon, is called sukla paksha , the dark half with the waning moon, which begins at the full moon and ends at the new moon is called krishna paksha .

The 15 days of the light half are counted from 1 to 15 and marked by a preceding "S" (for sukla - light); the 15 days of the dark half are counted from 1 to 14 and the last day with 30 and marked by a preceding "K" (for krishna - dark). In an amanta month, the first, light half is followed by the dark, second half, which explains the count K 30 for the last day of the month.

In a purnimanta month, the first, dark half is followed by the light, second half. Here, too, the last day of the dark half K 30 is counted, although it falls in the middle of the month.

Sometimes the individual lunar days are also referred to by names that are derived from the Indian numerals:

No.	Surname
1	pratipadâ
2	dvitîyâ
3	tŗitîyâ
4th	chaturtî
5	panchamî
6th	shasthî
7th	saptamî
8th	ashtamî
9	navamî
10	daśamî
11	ekâdasî
12	dvâdasî
13	trayôdasî
14th	chartudasî
15th	pûrņimâ
30th	amâvâsyâ

The civil month

The civil month begins with a new moon or full moon before the sun enters a new zodiac sign ( samkranti ).

It takes the sun an average of 30.43822963 days to move through a zodiac sign. Because of its uneven movement, the time fluctuates between 29.34806481 and 31.61057407 days. The moon needs an average of 29.53058796 days from new moon to new moon or full moon to full moon. Because of its uneven movement, the time fluctuates between 29.246 and 29.817 days.

Because of the different duration, it happens that a lunar month ends without the sun having entered a new zodiac sign. In this case, an additional civil month is switched on and the year comprises 13 months.

A month that is switched on is called adhika and precedes the actual ( nija ) month.

In addition, it happens - albeit rarely - that the sun completely traverses one sign of the zodiac and enters a second sign of the zodiac during a lunar month. In this case, a civil month is turned off.

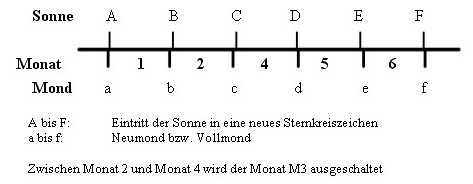
A month that is switched off is called kshaya . However, a bound lunar year always includes 12 or 13 civil months, so that sooner or later at least one civil month is inevitably switched on. The civil month has a length of 29 or 30 civil days (see below).

The month names

The month names are very old and have a long tradition.The individual months of the year have the following names in a chaitrada year:

month
Indian	German
चैत	Chaitra
वैशाख	Vaiśâkha
ज्येष	Jyeshtha
आषाढ	Asâdha
श्रावण	Śrâvana
भाद्रपद	Bhâdrapada
अश्विन्	Âśvina
कार्तिक	Karttika
मार्गशीर्ष	Agrahayana
पौष	Pausha
माघ	Mâgha
फाल्गुन	Phâlguna

In a karttikadi year the year begins with the month of Kârttika,

The day

The lunar day

A lunar month is the complete revolution of the moon around the earth in relation to the sun. During this orbit, the moon gains 360 ° distance from the sun in the course of a lunar month. A lunar day ( tithi ) is the time in which the moon gains 12 ° more distance from the sun. A lunar day lasts on average 23.62447222 hours.

The civil day

The civil day is counted after the lunar day on which sunrise falls.

Because of the uneven movement of the moon, however, the length of a lunar day varies widely; it fluctuates between 21.57333333 and 26.10666667 hours. Because of the different lengths of lunar day and civil day, it happens that a lunar day ends without a new civil day having started. In this case, a day is skipped in the day count; z. B. follows Wednesday S 3 Thursday S 5.

It also happens that two civil days begin during one lunar day. In this case, one day is counted twice when counting the day; z. B. follows Tuesday K 3 Wednesday K 3.

Division of the day

The civil day is divided into 60 gathas , these into 60 palas and these in turn into 60 vipalas . The following table contrasts gathas and hours and their subdivisions.

Indian	west
1 gathikâ = 60 pala	24 minutes
1 pala = 60 vipalas	24 seconds
1 vipala	0.4 seconds
west	Indian
1 hour	2 1/2 gathikâ
1 minute	2 1/2 pala
1 second	2 1/2 vipalas

Nakshatra

The orbit that the moon traverses in a sidereal month and for which the moon needs 27.32167361 days was already divided into 27 or 28 lunar houses ( nakshatra ) and named after the star constellation of the respective section. Today a division into 27 equally large sections of 13 ° 20 'each is common. The names of the lunar houses and their starting point are listed in the table below.

No.	Surname		Beginning
	Indian	transcription	Degree	Minutes
1	अश्विनी	âśhvinî	0 °
2	भरणी	bharaņî	13 °	20th
3	कृत्तिका	kŗittikâ	26 °	40
4th	रोहिणी	rohiņî	40 °
5	म्रृगशीर्षा	mŗigaśiras	53 °	20th
6th	आद्रा	ârdrâ	66 °	40
7th	पुनर्वसु	purnavasu	80 °
8th	पुष्य	pushya	93 °	20th
9	आश्ळेषा	âśhleshâ	106 °	40
10	मघा	maghâ	120 °
11	पूर्व फाल्गुनी	pûrvaphâlgunî	133 °	20th
12	उत्तर फाल्गुनी	uttaraphâlgunî	146 °	40
13	हस्त	haveâ	160 °
14th	चित्रा	chitrâ	173 °	20th
15th	स्वाति	svâti	186 °	40
16	विशाखा	viśâkhâ	200 °
17th	अनुराधा	anurâdhâ	213 °	20th
18th	ज्येष्ठा	jyeshthâ	226 °	40
19th	मूल / मूळ	mûlam	240 °
20th	पूर्वाषाढा	pûrvaashâdhâ	253 °	20th
21st	उत्तराषाढा	uttaraashâdhâ	266 °	40
22nd	श्रवण	śravaņa	280 °
23	श्रविष्ठा	śravishţhâ	293 °	20th
24	शतभिषक्	śatabhishaj	306 °	40
25th	पूर्वभाद्रपदा	pûrvabhâdrapada	320 °
26th	उत्तरभाद्रपदा	uttarabhâdrapada	333 °	20th
27	रेवती	revatî	346 °	40

yoga

A yoga is the time, move together in the sun and moon to a total of 13 ° 20 ', so by the length of a lunar house. Accordingly, there are 27 yogas . A yoga session lasts on average 22.59575 and varies between 20.88 and 24.60667 hours. The names of the yogas are listed in the following table

No.	Surname
1	vishkambha
2	prîti
3	ayushmat
4th	saubhâgya
5	śobhana
6th	atigaņda
7th	sukarman
8th	dhŗiti
9	śūla
10	gaņda
11	vŗiddhi
12	dhruva
13	vyâghâta
14th	harshaņa
15th	vajra
16	siddhi
17th	vyatîpâta
18th	varîyas
19th	parigha
20th	śiva
21st	siddha
22nd	sādhya
23	śubha
24	śukla
25th	brahman
26th	indra
27	vaidhŗti

Karana

A karana is the time in which the moon wanders through half a lunar house, i.e. half a tithi . In addition to four fixed names (1/1, 29/2, 30/1 and 30/2) there are seven names that are repeated several times. The following table gives the names of the 30 karanas and their assignment to the tithis :

tithi	1st half.		2nd half.		tithi	1st half.		2nd half
No.	Indian	Transcription	Indian	Transcription	No.	Indian	Transcription	Indian	Transcription
1	किंस्तुघ्न	kiṃstughna	बव	bava	16	बालव	bālava	कौलव	kaulava
2	बालव	bālava	कौलव	kaulava	17th	तैतिल	taitila	गरज	gara
3	तैतिल	taitila	गरज	gara	18th	वणिज	vaņij	भद्रा	viṣhţi
4th	वणिज	vaņij	भद्रा	viṣhţi	19th	बव	bava	बालव	bālava
5	बव	bava	बालव	bālava	20th	कौलव	kaulava	तैतिल	taitila
6th	कौलव	kaulava	तैतिल	taitila	21st	गरज	gara	वणिज	vaņij
7th	गरज	gara	वणिज	vaņij	22nd	भद्रा	viṣhţi	बव	bava
8th	भद्रा	viṣhţi	बव	bava	23	बालव	bālava	कौलव	kaulava
9	बालव	bālava	कौलव	kaulava	24	तैतिल	taitila	गरज	gara
10	तैतिल	taitila	गरज	gara	25th	वणिज	vaņij	भद्रा	viṣhţi
11	वणिज	vaņij	भद्रा	viṣhţi	26th	बव	bava	बालव	bālava
12	बव	bava	बालव	bālava	27	कौलव	kaulava	तैतिल	taitila
13	कौलव	kaulava	तैतिल	taitila	28	गरज	gara	वणिज	vaņij
14th	गरज	gara	वणिज	vaņij	29	भद्रा	viṣhṭi	शकुनि	śakuni
15th	भद्रा	viṣhṭi	बव	bava	30th	चतुष्पाद	chatuṣhpada	नाग	nâga

The week

The week

The week division is of Babylonian-Greek origin. The names are derived from the corresponding deities. The names are listed in the following table:

Indian		Gregorian
रविवार	Ravivār	Sunday
सोमवार	Somavār	Monday
मंगलवार	Mangalavār	Tuesday
बुधवार	Budhavār	Wednesday
गुरूवार	Guruvār	Thursday
शुक्रवार	Shukravār	Friday
शनिवार	Shanivār	Saturday

The calendar ( panchanga )

A Panchanga (literally: five parts), the traditional Hindu calendar, indicates tithi , nakshatra , yoga and karana for every day in addition to the day of the week for the time of sunrise .

See also

• List of calendar systems
• Indian national calendar

literature

• Friedrich Karl Ginzel Handbook of Mathematical and Technical Chronology. Vol. 1: Calendar of the Babylonians, Egyptians, Mohammedans, Persians, Indians, Southeast Asians, Chinese, Japanese and Central Americans , Leipzig 1906 [Reprint of the original edition, University of Innsbruck, undated] - (online in Internet Archive )
• Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar , London 1896 ( as PDF file )
• Edward M. Reingold / Nachum Dershowitz, Calendrical Calculations - The Millennium Edition , Cambridge 2001 (English)
• Reingold / Nachum Dershowitz, Indian Calendrical Calculations ( as PDF file ) (English)
• Leow Choon Lian, Indian Calendars, National University of Singapore, 2000/2001 ( as PDF file ) (English)

Web links

• Holger Oertel: Calendar in India
• Bernhard Peter: Indian calendar - overview of the different systems

Individual evidence

1. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 334 f
2. ^ Edward M. Reingold / Nachum Dershowitz: Calendrical Calculations - The Millennium Edition , Cambridge 2001, p. 127
3. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 351
4. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 347
5. ↑ Leow Choon Lian: Indian Calendars , National University of Singapore, 2000/2001, p. 36
6. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 341
7. ↑ Edward M. Reingold / Nachum Dershowitz, Indian Calendrical Calculations ( Memento of the original from March 21, 2015 in the Internet Archive ) Info: The  archive link has been inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. , P. 14
8. ↑ Details of years , accessed November 9, 2014.
9. ↑ Leow Choon Lian: Indian Calendars , National University of Singapore, 2000/2001, pp. 40f.
10. ^ Menninger: number and number , Vandenhoeck & Ruprecht, Göttingen 1958, Volume 1, p. 103
11. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, pp. 348f.
12. ^ ^{A b} Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 342.
13. ↑ Leow Choon Lian: Indian Calendars , National University of Singapore, 2000/2001, p. 38.
14. ↑ Leow Choon Lian: Indian Calendars , National University of Singapore, 2000/2001, p. 42
15. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 320
16. ^ ^{A b} Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 349.
17. ↑ Leow Choon Lian: Indian Calendars , National University of Singapore, 2000/2001, p. 41
18. ↑ ^{a b} Robert Sewell / Sankara Balkrishna Dikshit: The Indian Calendar , London 1896, p. 2.
19. ^ Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar , London 1896, p. 21
20. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 328
21. ^ Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar , London 1896, p. 3
22. ^ Friedrich Karl Ginzel: Handbook of mathematical and technical chronology, Leipzig 1906, Vol. I, pages 361f.
23. ^ Friedrich Karl Ginzel: Handbook of the mathematical and technical chronology. Vol. 1, Leipzig 1906, p. 360