Isoclinic

The term isocline (from the Greek ísos = equal and klínein = incline) means in mathematics and geophysics a curve of equal inclination.

Isoclines in Mathematics

In mathematics , isoclines are an aid for graphic integration , i.e. for the graphic determination of approximate solutions of a differential equation .

For an explicit differential equation , any curve with an equation of the type (at constant ) is an isocline. At the intersections of different solution curves of the differential equation with this isocline, these solution curves have the same slope (namely ) and thus the same angle of inclination with respect to the axis. ${\displaystyle y'=f(x,y)}$ ${\displaystyle f(x,y)=C}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle x}$

example

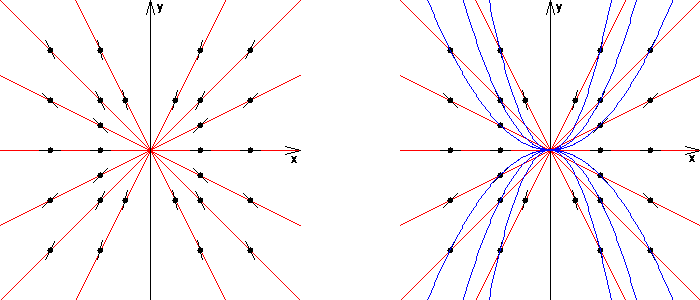
For the differential equation , an isocline equation reads or . The isoclines in this example are the straight lines through the origin with the exception of the axis. The solutions of the differential equation have (at least locally) the form . The corresponding solution curves are for parabolas ; for one receives the -axis as a further solution curve. ${\displaystyle y'={\tfrac {2y}{x}}}$ ${\displaystyle {\tfrac {2y}{x}}=C}$ ${\displaystyle y={\tfrac {C}{2}}x}$ ${\displaystyle y}$ ${\displaystyle y=Cx^{2}}$ ${\displaystyle C\neq 0}$ ${\displaystyle C=0}$ ${\displaystyle x}$

The two sketches show some of the isoclines (red). The associated gradient can be read from the short straight sections ( line elements ). Some solution curves (blue) are also shown in the sketch on the right.

Isoclines in geophysics

In geophysics , the term isocline is used for lines of equal magnetic inclination . Such an isocline connects points with each other at which the field lines of the earth's magnetic field enclose the same angle to the earth's surface.

Zero kline

The zero kline represents a special case for which applies . ${\displaystyle f(x,y)=C=0}$

See also

• Isoline